§1 单纯形表的灵敏度分析 原始的约束方程组:Ax=b 迭代,对原系数矩阵进行初等行变换,变成以B为 基的最终单纯形表,即对原来约束方程组左乘B1: BAx=Bb 原始的最终单纯形表中系数矩阵: BA 原始的最终单纯形表中基变重xB的胖y
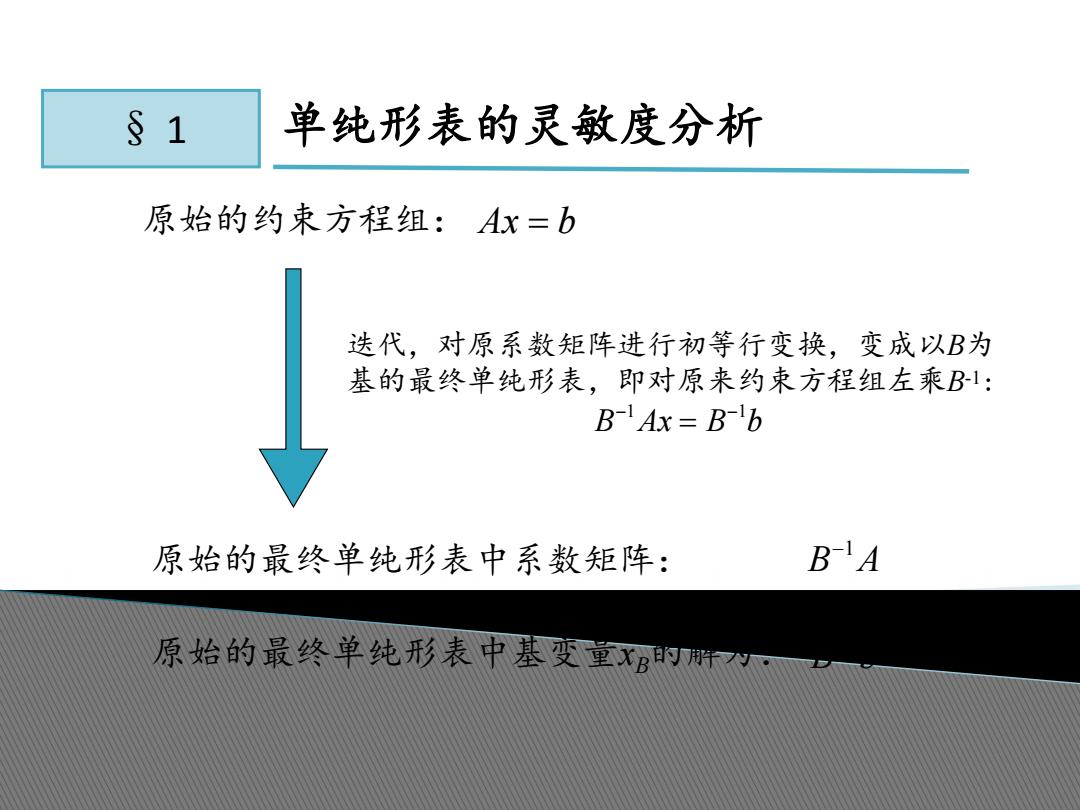
§ 1 单纯形表的灵敏度分析 原始的约束方程组: Ax b 迭代,对原系数矩阵进行初等行变换,变成以B为 基的最终单纯形表,即对原来约束方程组左乘B-1: 1 1 B Ax B b 原始的最终单纯形表中系数矩阵: 1 B A 原始的最终单纯形表中基变量xB的解为: 1 B b

§1 单纯形表的灵敏度分析 0 b2 0 bk→bk+△bE b→b'=b+△b= △b 0 0 原始的最终单纯形表中基变量xB变为x'B: xB=B'(b+△b)=xB+BAb=xB+Dk·Ab 其中D为B1的第k列,D=
§ 1 单纯形表的灵敏度分析 k k k b b b 1 2 0 0 0 0 k k m b b b b b b b b b 原始的最终单纯形表中基变量xB变为x' B: 1 1 B ( k ) B k = B k k x B b b x B b x D b 其中Dk为B-1的第k列, 1 2 = k k k mk d d D d
§1 单纯形表的灵敏度分析 为使新的基本解x'的各分量均非负即: dix xB1+△b·dk 使得对应约束条件 dix 的对偶价格不变 .: △b= xB2+△b·d2k ≥ 0 X Bm d'mk xBm+Ab·dik max d>0≤Ab≤min
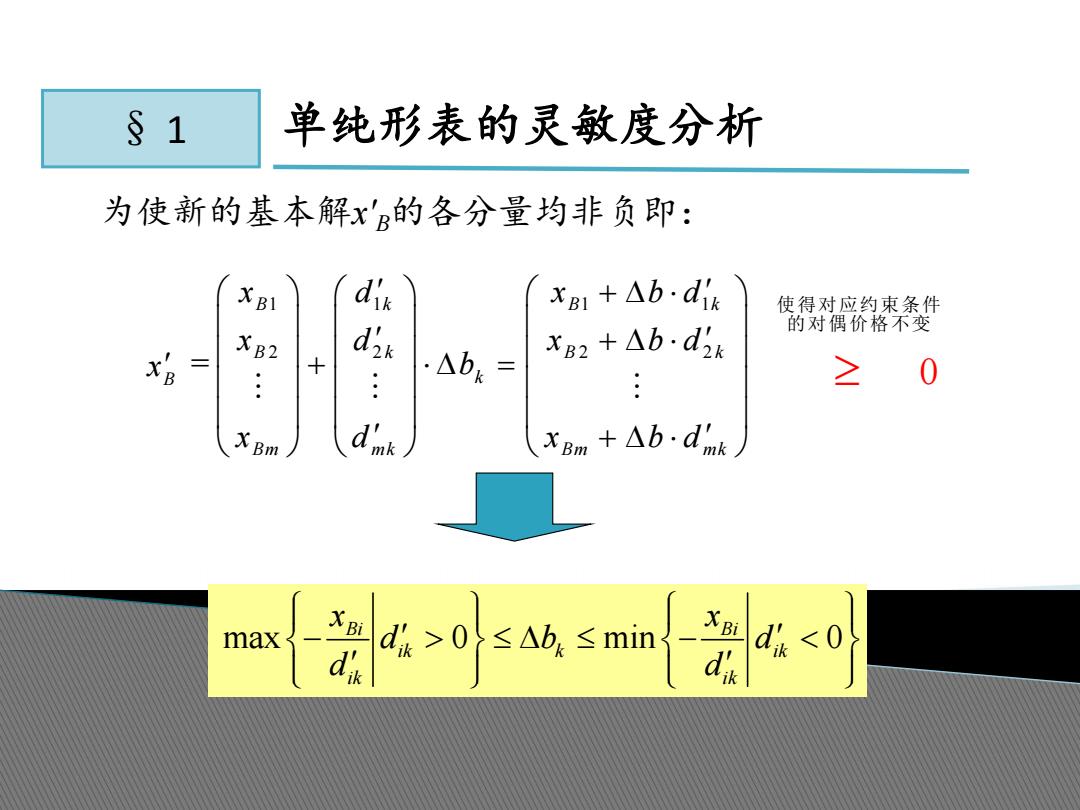
§ 1 单纯形表的灵敏度分析 1 1 1 1 2 2 2 2 = 0 B k B k B k B k B k Bm mk Bm mk x d x b d x d x b d x b x d x b d 使得对应约束条件 的对偶价格不变 为使新的基本解x' B的各分量均非负即: max 0 min 0 Bi Bi ik k ik ik ik x x d b d d d
§1 单纯形表的灵敏度分析 以第二章例1在最终单纯形表上对进行b灵敏度分析: 迭代 基变 x1 X2 S1 S2 S3 比值 次数 量 CB b 50 100 0 0 0 blaj X1 50 0 1 0 -1 50 S2 0 0 0 -2 1 50 2 X2 100 0 0 0 1 250 防 50 100 50 0 50 27500 0=C 0 -50 0 -50 大一 击云山合右h亦旦。 甘士六6h五为(100)工 xB为宋赤,0义25泸设净盒时数传3m 条件即设备台时数的对傅价格不变,都为季设备台时50元。 -50≤△b,≤25,250≤b+△h≤325 时第1个约束条件的对偶价格不变
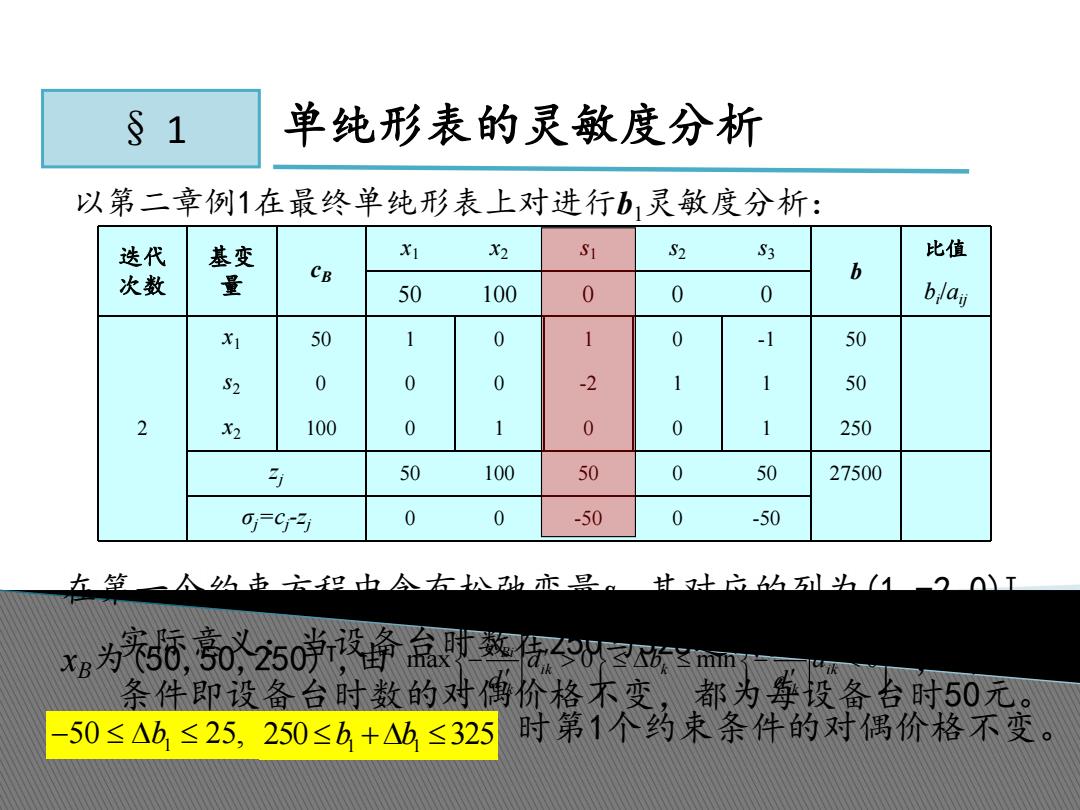
§ 1 单纯形表的灵敏度分析 以第二章例1在最终单纯形表上对进行b1灵敏度分析: 迭代 次数 基变 量 cB x1 x2 s1 s2 s3 b 比值 50 100 0 0 0 bi/aij 2 x1 50 1 0 1 0 -1 50 s2 0 0 0 -2 1 1 50 x2 100 0 1 0 0 1 250 zj 50 100 50 0 50 27500 σj=cj-zj 0 0 -50 0 -50 在第一个约束方程中含有松弛变量s1,其对应的列为(1,-2,0)T , xB为(50,50,250) T ,由 ,得到 时第1个约束条件的对偶价格不变。 max 0 min 0 Bi Bi ik k ik ik ik x x d b d d d 1 50 b 25, 1 1 250b b 325 实际意义:当设备台时数在250与325之间变化时,该约束 条件即设备台时数的对偶价格不变,都为每设备台时50元

§1 单纯形表的灵敏度分析 三、约束方程系数矩阵A灵敏度分析 1.最终单纯形表上x是非基变量 x的初始单纯形表的系数列P 迭代→p >的餐纯酸凌变化,其他均不变 新的系数列:Bp 'k:CBBpk OkCk-CB∵Bpk 若σ'≤0,则原最优解仍然为最优解。若σ⊙U 代以求出最优
§ 1 单纯形表的灵敏度分析 三、约束方程系数矩阵 A 灵敏度分析 1.最终单纯形表上xk是非基变量 xk的初始单纯形表的系数列 k k p p 迭代 Ø xk的系数列、zk以及σk变化,其他均不变 最终单纯形表中 新的系数列 : z' k : σ' k : -1 k B p -1 B k c B p -1 k B k c c B p 若σ' k≤0,则原最优解仍然为最优解。若σ' k>0,则继续进行迭 代以求出最优