
8.2群的定义与性质 3.群的性质 ·定理8.5:设<G,*>为群,则 (1):方程a*x=b,y*a=b在G中有解且有唯一解; (2):当G≠{e时,无零元; (3):G中所有元素都是可约的,即Va,x,y∈G,有 a*x=a*y=>x=y,x*a=y*a=>x=y; (4):运算表中任意一行(列)都没有两个相同的元素; (5):群G中除么元e外无其它幂等元。 16/73
16/73 8.2 群的定义与性质 • 3.群的性质 •定理8.5:设<G,*>为群,则 (1):方程a*x=b,y*a=b在G中有解且有唯一解; (2):当 时,无零元; (3):G中所有元素都是可约的,即 ,有 a*x=a*y=>x=y,x*a=y*a=>x=y; (4):运算表中任意一行(列)都没有两个相同的元素; (5):群G中除幺元e外无其它幂等元。 G {e} a, x, y G

8.2群的定义与性质 证:(1)先证a1*b是方程a*x=b的解:代入,则 a*(a*b)=(a*a1)*b=b, 再证唯一性:设c为方程a*x=b的解,即a*c=b,则 c=e*c=(a*a)*c=a*(a*c)=a-*b 同理b*a是方程y*a=b的唯一解 (2)若G有零元,且G≠{,则|G≥2,由定理7.5,知零元无逆元 与G为群矛盾 (3)x=e*x=(a*a)*x=a*(a*x)=a*(a*y)=(a*a)*y=e*y (4)反证法:设某一行有两个相同元素,设为a,行的表头为b, 列的表头分别为c,c2,显然c≠c2,而a=bC=bc2→C1=c2,矛盾 (⑤)反证法:设a是G中非么的幂等元,即a*a=a,且a≠e,因此 a*a=a*e,由(3)得a=e,矛盾 1773
17/73 8.2 群的定义与性质 ,由 得 ,矛盾 反证法:设 是 中非幺的幂等元,即 ,且 ,因此 列的表头分别为 ,显然 ,而 ,矛盾 反证法:设某一行有两个相同元素,设为 ,行的表头为 , 与 为群矛盾 若 有零元,且 ,则 ,由定理 ,知零元无逆元 同理 是方程 的唯一解 再证唯一性:设 为方程 的解,即 ,则 证: 先证 是方程 的解:代入,则 a a a e a e a a a a a e c c c c a bc bc c c a b x e x a a x a a x a a y a a y e y G G e G b a y a b c e c a a c a a c a b c a x b a c b a a b a a b b a b a x b = = = = = = = = = = = = = = = = = = = = = = − − − − − − − − − − − (3) (5) G , (4) (3) ( ) ( ) ( ) ( ) (2) G { } | | 2 7.5 * ( ) ( ) ( ) ( ) , (1) 1 2 1 2 1 2 1 2 1 1 1 1 1 1 1 1 1 1 1
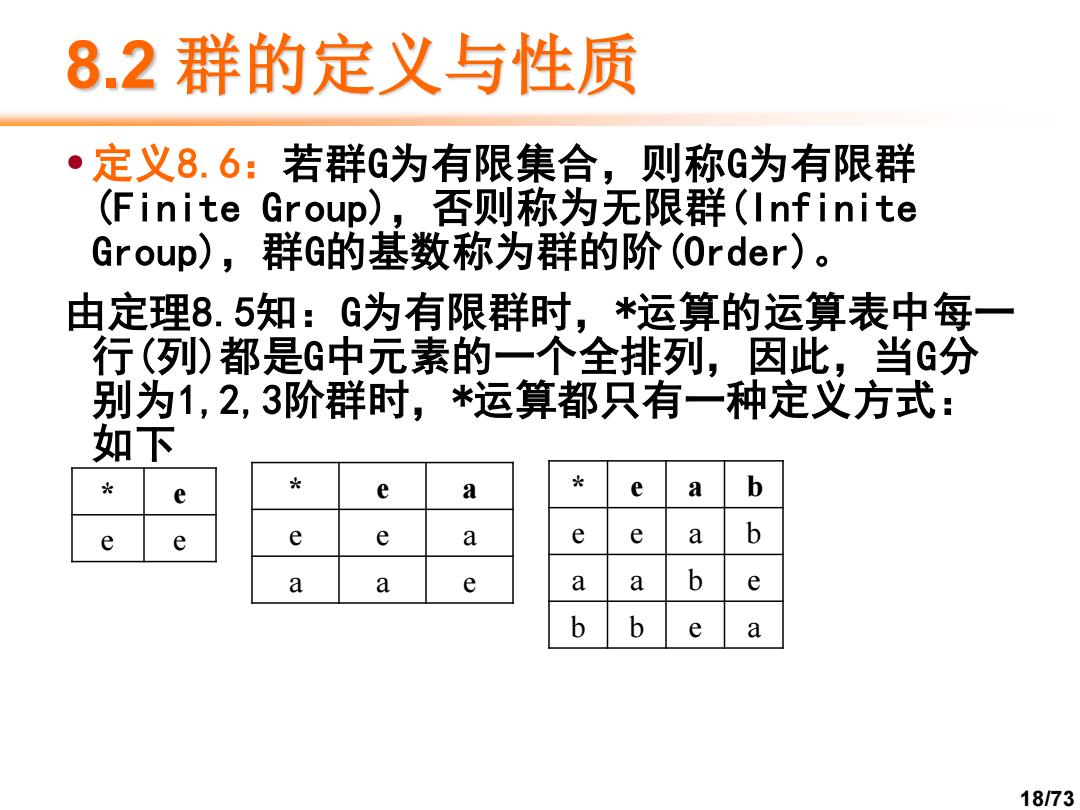
8.2群的定义与性质 定义8.6:若群G为有限集合,则称G为有限群 (Finite Group),否则称为无限群(Infinite Group),群G的基数称为群的阶(Order) 由定理8.5知:G为有限群时,*运算的运算表中每一 行(列)都是G中元素的一个全排列,因此,当G分 别为1,2,3阶群时,*运算都只有一种定义方式: 如下 头 光 e e a 光 e a b e e e e a e e a b a a e a a b e b b e a 18/73
18/73 8.2 群的定义与性质 •定义8.6:若群G为有限集合,则称G为有限群 (Finite Group),否则称为无限群(Infinite Group),群G的基数称为群的阶(Order)。 由定理8.5知:G为有限群时,*运算的运算表中每一 行(列)都是G中元素的一个全排列,因此,当G分 别为1,2,3阶群时,*运算都只有一种定义方式: 如下 * e e e * e a e e a a a e * e a b e e a b a a b e b b e a

8.2群的定义与性质 ●4.元素的阶及性质 定义8.7:设<G,>为群,a∈G,满足等式a”=e ● 的最小正整数n称为a的阶(0rder)或周期,记作 |a=n,若不存在这样的正整数n, 称a是无限阶。 例:()任何群G的么元e的阶为1,且只有幺元的阶 为1; (2)<Z,+>中幺元0的阶为1,其它整数均为无限阶元 (3)<Z4,+4>中[1]的阶为4,[2]的阶为2,[3]的阶 为4。 定理8.6:有限群G的每个元素都有有限阶,且其 阶数不超过群G的阶数G。 19/73
19/73 8.2 群的定义与性质 •4.元素的阶及性质 •定义8.7:设<G,*>为群, ,满足等式 的最小正整数n称为a的阶(Order)或周期,记作 |a|=n,若不存在这样的正整数n,称a是无限阶。 例:(1)任何群G的幺元e的阶为1,且只有幺元的阶 为1; (2)<Z,+>中幺元0的阶为1,其它整数均为无限阶元 (3) 中[1]的阶为4,[2]的阶为2,[3]的阶 为4。 • 定理8.6:有限群G的每个元素都有有限阶,且其 阶数不超过群G的阶数|G|。 aG a e n = Z4 ,+4

8.2群的定义与性质 证:设a为G的任一元素,考虑e=a°,d,a2,…,a这G+1个 G中的元素,由于G中只有G个元素,由鸽巢原理 它们中至少有2个是同一元素,不妨设:a=a(0≤s<t≤G) 于是as=e,因此a有有限阶,且阶数是t-s,且不超过|G引 ● 定理8.7:设<G,*>为群,a∈G,且|a=r,设k为整 数,则 (1)a=e当且仅当rk (2)aal 20/73
20/73 8.2 群的定义与性质 •定理8.7:设<G,*>为群, ,设k为整 数,则 (1) (2) | | . 2 (0 | |) | | , , , , | | 1 0 1 2 | | a e a t s G a a s t G G G G a G e a a a a G t s s t G 于是 ,因此 有有限阶,且阶数是 ,且不超过 它们中至少有 个是同一元素,不妨设: 中的元素,由于 中只有 个元素,由鸽巢原理, 证:设 为 的任一元素,考虑 这 个 = − = = + − aG,且| a |= r a e r k k = 当且仅当 | | | | | 1 a = a −