
式中 hk)=【zk-1,-zk-nbk-以,-n o=a az,anbb,bno (3.15) 对于=1,2,,L,方程(3.14)构成一个线性方程组,可以把它写成 2(k)=Hz(k)9+e(k) (3.16) 其中 (3.17) 另外,设模型(3.14)的噪声(完全可以用一阶和二阶统计矩 阵描述,即设它的均值矩阵和协方差矩阵分别为 16 20241420
2024/4/20 16 (3.15) (3.16) (3.17) 式中 ( ) ( ) ( ) ( ) ( ) T n n T a b a a a b b b h k z k z k n u k u k n , , , , , , , 1 , , , 1 , , 1 2 1 2 = = − − − − − − 对于k=1,2,...,L,方程(3.14)构成一个线性方程组,可以把它写成 z (k) H (k) e (k) L = L + L 其中 () () () () () () ()()()() ()()()() ()()()() −−−−−− −−− − −−− − = = = a b a b a b L L L zLzLnuLuLn zznuun zznuun H eL e e e zL z z z 1 1 12 12 01 01 2 1 2 1 ,, 另外,设模型(3.14)的噪声e(k)完全可以用一阶和二阶统计矩 阵描述,即设它的均值矩阵和协方差矩阵分别为
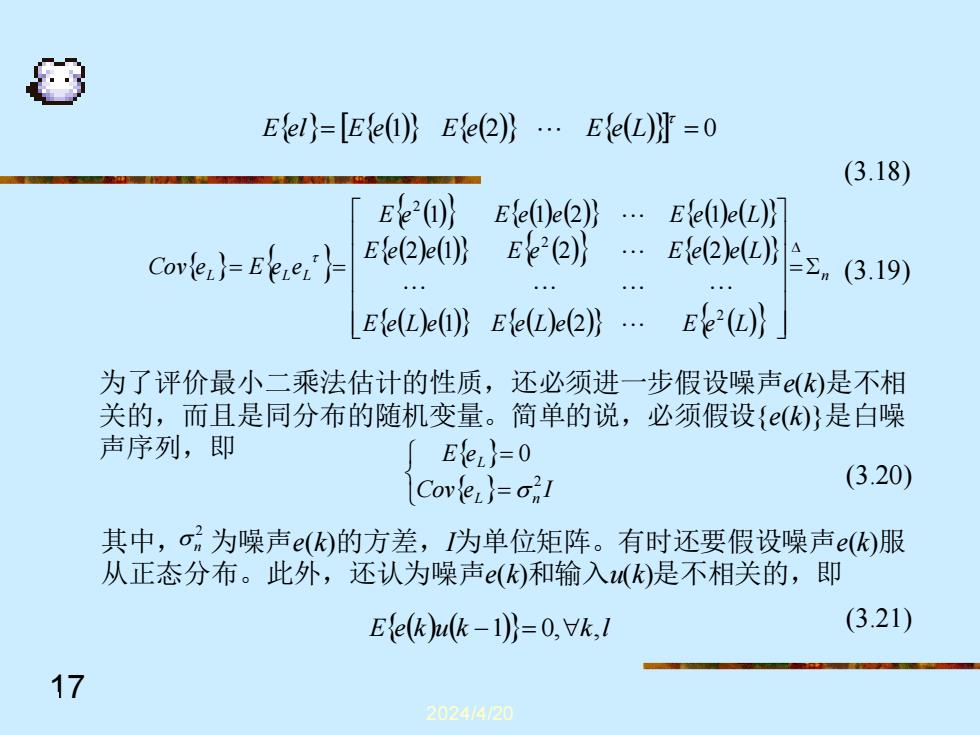
Eel=[Ee(1 Efe(2...Efe(L0 (3.18) Ee20} E{e①)e(2)} E{e(①)e(L)} Coe}=Eee,'}片 E{e(2)e@} Ee22)} E{e(2)e(L} =2m(3.19) EeLe1) EeL)e(2)}. Ee(L) 为了评价最小二乘法估计的性质,还必须进一步假设噪声(是不相 关的,而且是同分布的随机变量。简单的说,必须假设{(}是白噪 声序列,即 Ee}=0 Cove)=a2l (3.20) 其中,o7为噪声e(的方差,为单位矩阵。有时还要假设噪声e(化服 从正态分布。此外,还认为噪声(化和输入(是不相关的,即 Efe(k)u(k-1)}=O,Vk,1 (3.21) 17 202414120
2024/4/20 17 = (1) (2) ( ) = 0 E el E e E e E e L (3.18) (3.19) (3.20) (3.21) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) L L L n E e L e E e L e E e L E e e E e E e e L E e E e e E e e L Cov e E e e = = = 2 2 2 1 2 2 1 2 2 1 1 2 1 为了评价最小二乘法估计的性质,还必须进一步假设噪声e(k)是不相 关的,而且是同分布的随机变量。简单的说,必须假设{e(k)}是白噪 声序列,即 其中, 为噪声e(k)的方差,I为单位矩阵。有时还要假设噪声e(k)服 从正态分布。此外,还认为噪声e(k)和输入u(k)是不相关的,即 = = Cov e I E e L n L 2 0 2 n Ee(k)u(k −1)= 0,k,l

最后,如何选择数据长度也是要考虑的问题。显 然,联立方程组(3.16)具有L个方程,包括(n+nb)个未 知数。如果L≤nn,方程的个数少于未知数个数, 模型参数不能唯一确定,这种情况一般可以不去考虑 它。如果L=(n+n),则只有当e=0时,0才有唯一的确 定解。当不等于0时,A只有取L>≥nn,才有可能 确定一个“最优”的模型参数0,而且为了保证辨识的精 度,L必须充分大。 18 202414/20
2024/4/20 18 最后,如何选择数据长度也是要考虑的问题。显 然,联立方程组(3.16)具有L个方程,包括(na+nb )个未 知数。如果L<(na+nb ),方程的个数少于未知数个数, 模型参数不能唯一确定,这种情况一般可以不去考虑 它。如果L=(na+nb ),则只有当eL=0时,θ才有唯一的确 定解。当eL不等于0时,θ只有取L>(na+nb ),才有可能 确定一个“最优”的模型参数θ,而且为了保证辨识的精 度,L必须充分大

色 本小节结束了! 19 202414120
2024/4/20 19

3.3最小二乘问题的一次完成算法 33.1普通最小三乘问题的解 考虑模型 z(k)=h"(k)0+e(k) (3.22) 的辨识问题,其中z(和()都是可观测数据,是待估计参数,去准 则函数 =2[-2[)-M肉0]=-H,ora-H,0) (3.23) 极小化〔0,求得参数的估计值,将使模型的输出最好地预报系统的 输出。 设0使得J@as=mn,则有 (3.24) 展开上式,并运用如下两个向量微分公式 小a (3.25) 20 202414120
2024/4/20 20 3.3 最小二乘问题的一次完成算法 3.3.1 普通最小二乘问题的解 考虑模型 的辨识问题,其中z(k)和h(k)都是可观测数据,θ是待估计参数,去准 则函数 z(k) = h (k) + e(k) (3.22) (3.23) (3.25) (3.24) ( ) ( ) 2 2 1 1 ( ) ( ) ( ) ( ) L L T T L L L L k k J z k z k k = = = = − = − − θ h θ z H θ z H θ 极小化J(θ),求得参数θ的估计值,将使模型的输出最好地预报系统的 输出。 设 ˆ LS 使得 J ( ) LS = min ,则有 ( ) ( − ) ( − ) = 0 = L L L HL z H z J LS 展开上式,并运用如下两个向量微分公式 ( ) a x a x =