
四.倒易点阵实例: 倒格子基矢是从点阵基矢引出的,它们之间的联系需要我 们通过具体实例来理解:根据右面定义, a,xa b=2 显然:b1⊥2,a3,b2⊥a3,a1, a·(a2×a3) i3⊥a1,a2, 6,=2 a3×a1 a·(a2×a3) b3=2π a1×a2 a1(a2×a)) 左图是一个二维斜方点阵和它的 倒易点阵,b1⊥a2,b2⊥a1, b,a,=a,b=2元 b b1a2=b2a1=0
倒格子基矢是从点阵基矢引出的,它们之间的联系需要我 们通过具体实例来理解:根据右面定义, 四. 倒易点阵实例: ( ) ( ) ( ) 1 2 3 1 2 3 1 2 3 3 1 2 1 2 3 2 3 1 2 2 2 a a a a a b a a a a a b a a a a a b K K K K K K K K K K K K K K K K K K ⋅ × × = ⋅ × × = ⋅ × × = π π π 显然 : a1 G a 2 G b1 G b 2 G 左图是一个二维斜方点阵和它的 倒易点阵, b ab a 1 22 1 ⊥ ⊥ , , G GG G 22 1 1 ba ab = = 2 π G G G JG i i ba ba 12 21 = = 0 G G GG i i 1 2 32 31 3 12 ,, ,, , , b aab aa b aa ⊥ ⊥ ⊥ G GGG GG G GG

简立方点阵:一 倒易点阵仍是简立方点阵: a ai,a,aj,a,ak 6-2ia-2j.6-2无 a 所以倒格子也是布拉菲格子。 六角点阵: 六角点阵的倒易点阵: 见Ashcroft p88 c轴方向不变,a 轴在垂直于c轴的 c 平面上旋转30度。 a 160° a 60° (a) (b)
简立方点阵: 12 3 a ai a a == = , ,j a ak GGG 倒易点阵仍是简立方点阵: 12 3 22 2 b ib jb k ,,, aa a π π π == = G G G 六角点阵的倒易点阵: 见Ashcroft p88 六角点阵: c 轴方向不变,a 轴在垂直于c 轴的 平面上旋转30度。 所以倒格子也是布拉菲格子
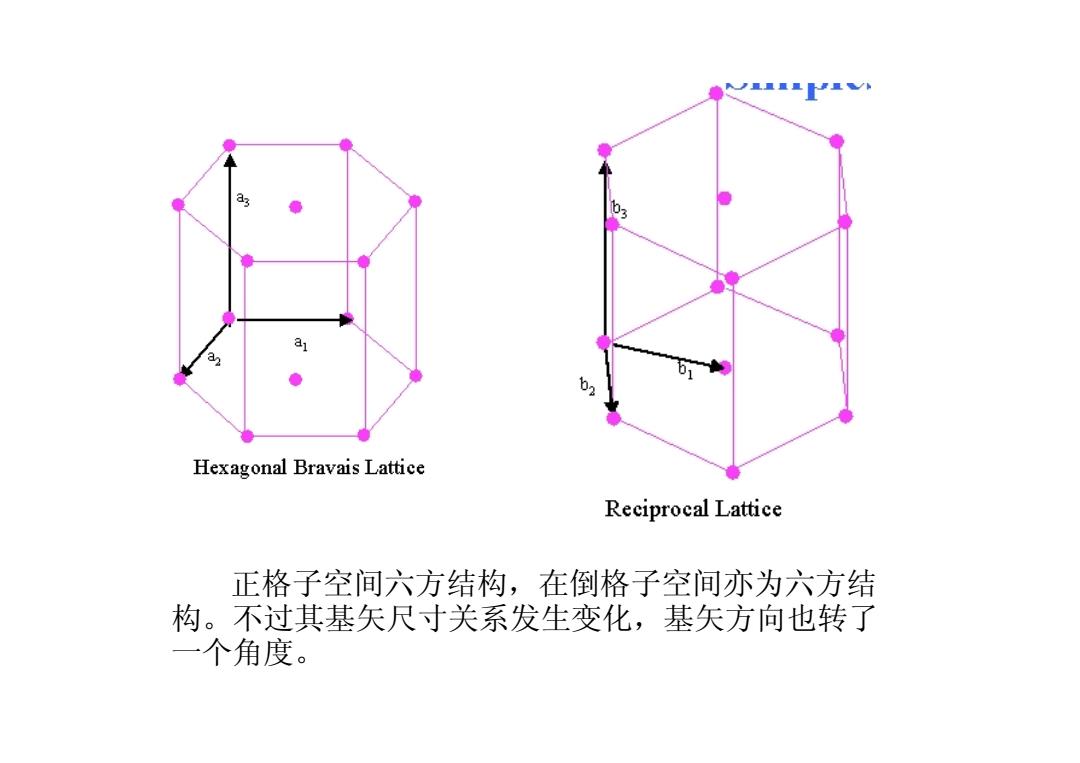
Hexagonal Bravais Lattice Reciprocal Lattice 正格子空间六方结构,在倒格子空间亦为六方结 构。不过其基矢尺寸关系发生变化,基矢方向也转了 一个角度
正格子空间六方结构,在倒格子空间亦为六方结 构。不过其基矢尺寸关系发生变化,基矢方向也转了 一个角度

三维例子: Direct space 正点阵为简 Reciprocal space 单点阵,倒 易点阵也是 简单点阵。 正格子空间中长 的基矢a3对应于 倒格子空间短的 b. 基矢b3,反之亦 然。推广,正格 子空间长的线条 Simple Orthorhombic Bravais Lattice Reciprocal Lattice 对应于倒格子空 with as>a>a Note:b >b2>b3 间短的线条
正格子空间中长 的基矢 a 3对应于 倒格子空间短的 基矢 b 3,反之亦 然。推广,正格 子空间长的线条 对应于倒格子空 间短的线条。 三维例子: 正点阵为简 单点阵,倒 易点阵也是 简单点阵

正点阵为有心点阵时,倒易点阵也是有心点阵, 但有心类型可能不同,例如:体心立方点阵的倒格子 为面心立方点阵。 a 2πda Primitive vectors and the conventional cell of bee lattice Reciprocal lattice is Face Centered Cubic
正点阵为有心点阵时,倒易点阵也是有心点阵, 但有心类型可能不同,例如:体心立方点阵的倒格子 为面心立方点阵