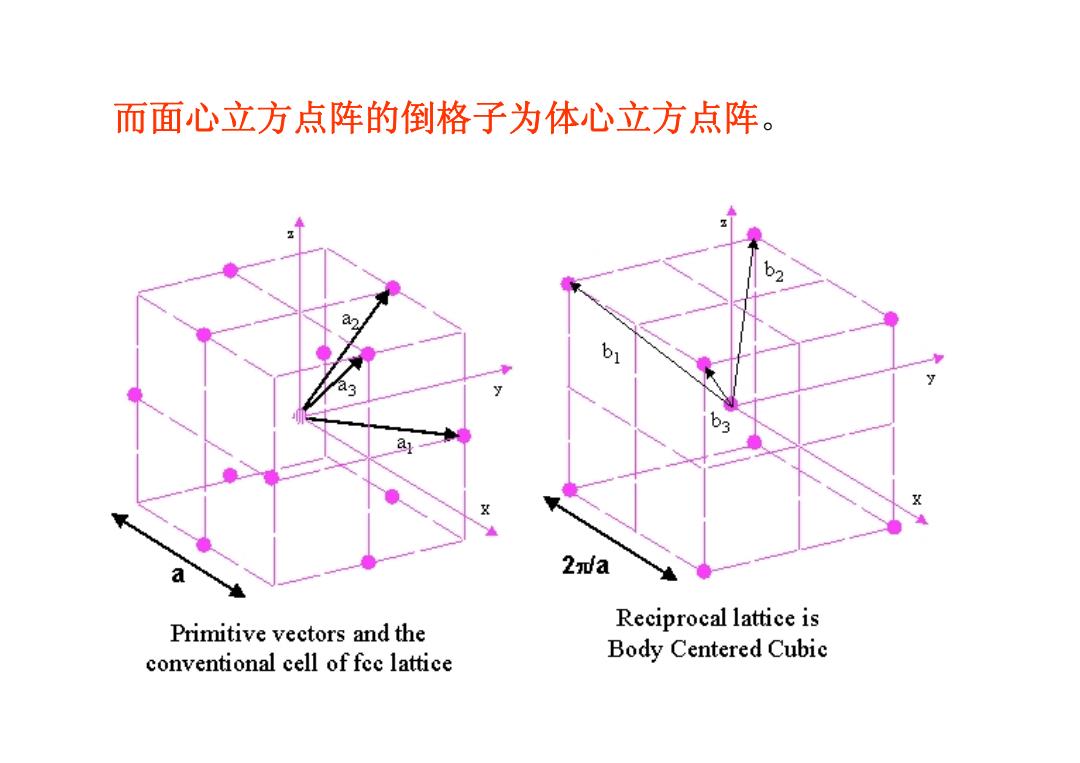
而面心立方点阵的倒格子为体心立方点阵。 a a 2πa Reciprocal lattice is Primitive vectors and the conventional cell of fee lattice Body Centered Cubic
而面心立方点阵的倒格子为体心立方点阵
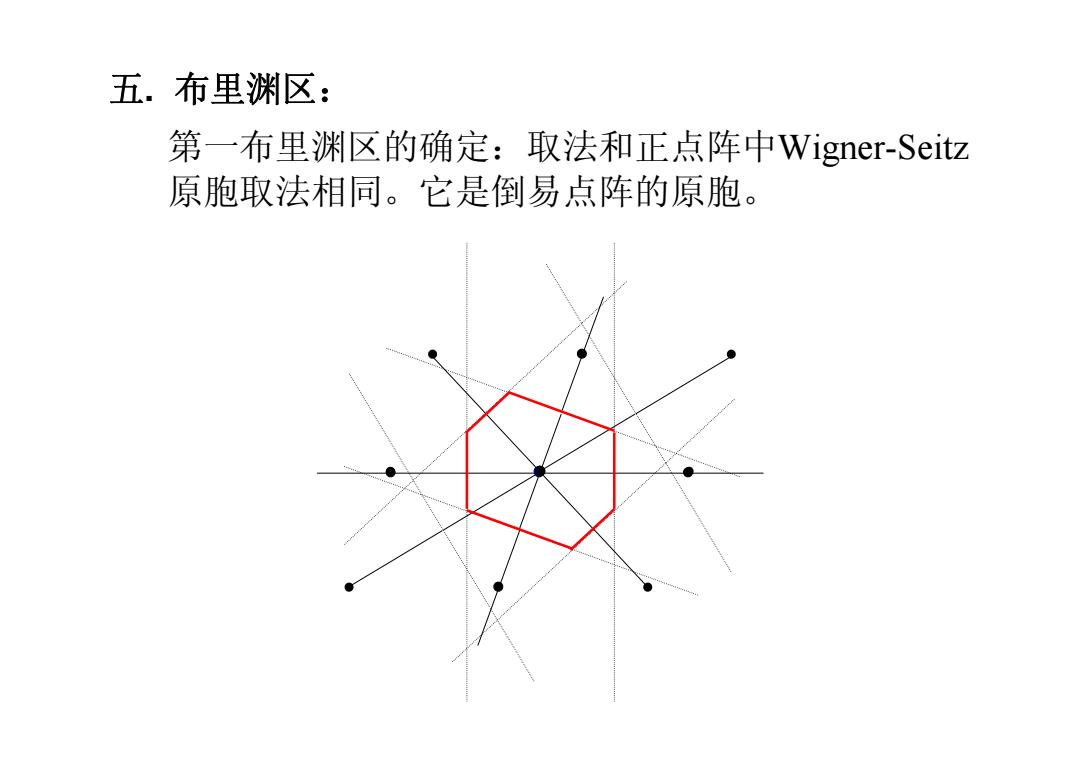
五.布里渊区: 第一布里渊区的确定:取法和正点阵中Wigner--Seitz 原胞取法相同。它是倒易点阵的原胞
第一布里渊区的确定:取法和正点阵中Wigner-Seitz 原胞取法相同。它是倒易点阵的原胞。 五. 布里渊区:

布里渊区定义:在倒易点阵中,以某一格点为坐标原点,做所有 倒格矢的垂直平分面,倒易空间被这些平面分成许多包围原 点的多面体区域,这些区域称作布里渊区,其中最靠近原点 的平面所围成的区域称作第一布里渊区,第一布里渊区界面 与次远垂直平分面所围成的区域称作第二布里渊区,依次类 推得到二维正方格子的布里渊区图见下页。 由于布里渊区界面是某倒格矢G的垂直平分面,如果 用k表示从原点出发、端点落在布里渊区界面上的倒易空 间矢量,它必然满足方程:G=G2 该方程称作布里渊区的界面方程
布里渊区定义:在倒易点阵中,以某一格点为坐标原点,做所有 倒格矢的垂直平分面,倒易空间被这些平面分成许多包围原 点的多面体区域,这些区域称作布里渊区,其中最靠近原点 的平面所围成的区域称作第一布里渊区,第一布里渊区界面 与次远垂直平分面所围成的区域称作第二布里渊区,依次类 推得到二维正方格子的布里渊区图见下页。 由于布里渊区界面是某倒格矢 的垂直平分面,如果 用 表示从原点出发、端点落在布里渊区界面上的倒易空 间矢量,它必然满足方程: G JG k G 1 2 2 kG G = G JG i 该方程称作布里渊区的界面方程
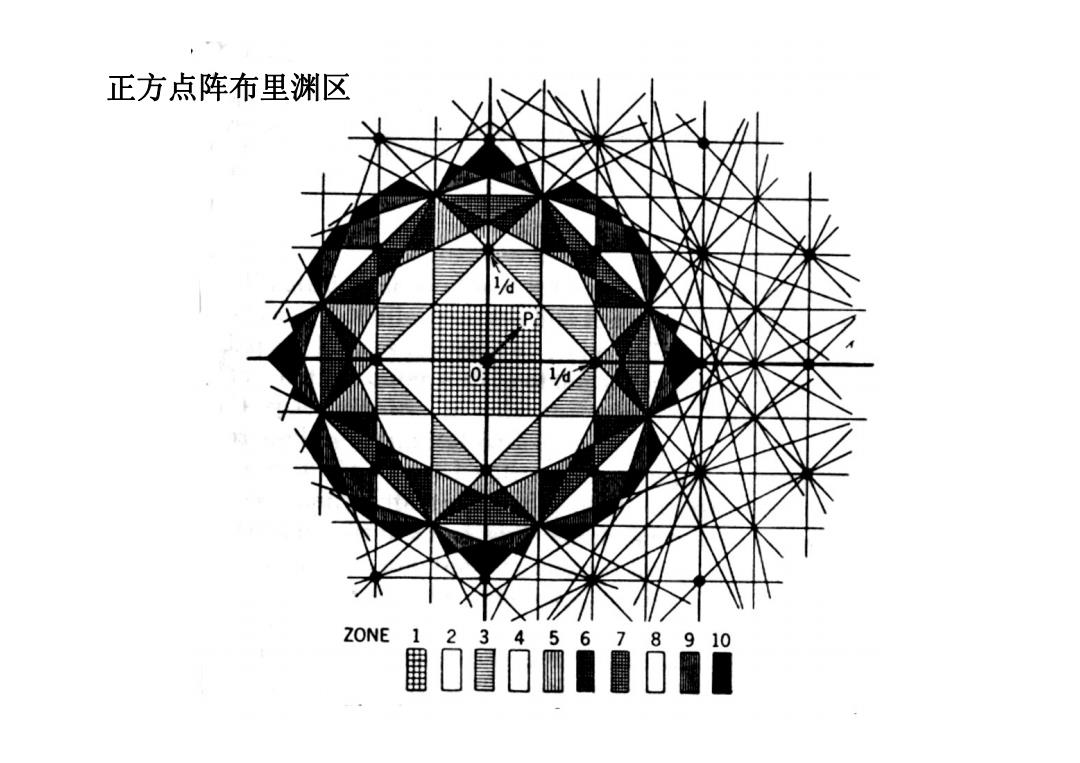
正方点阵布里渊区 Z0NE12345678910 圃0 冒00
正方点阵布里渊区
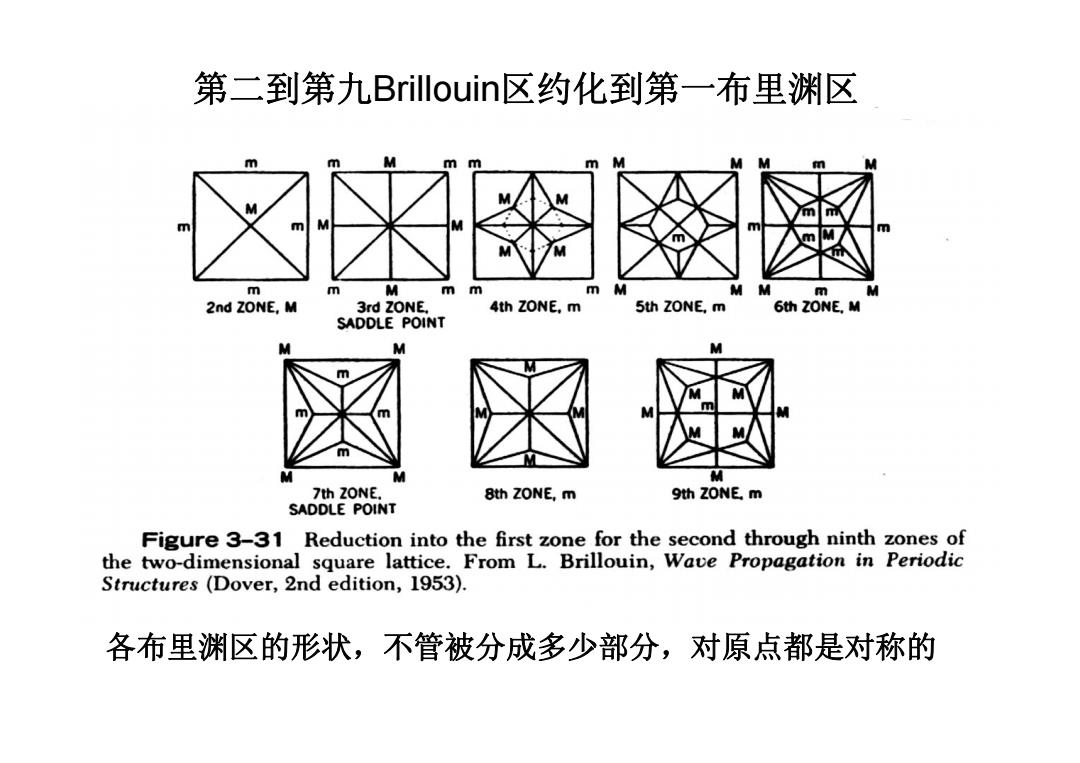
第二到第九Brillouin区约化到第一布里渊区 m m M m m m M M m M m m M mm mM 2nd ZONE,M 3rd ZONE, 4th ZONE,m 5th ZONE,m 6th ZONE.M SADDLE POINT M m m m m M M 7th ZONE. 8th ZONE,m 9th ZONE,m SADDLE POINT Figure 3-31 Reduction into the first zone for the second through ninth zones of the two-dimensional square lattice.From L.Brillouin,Wave Propagation in Periodic Structures (Dover,2nd edition,1953). 各布里渊区的形状,不管被分成多少部分,对原点都是对称的
第二到第九Brillouin区约化到第一布里渊区 各布里渊区的形状,不管被分成多少部分,对原点都是对称的