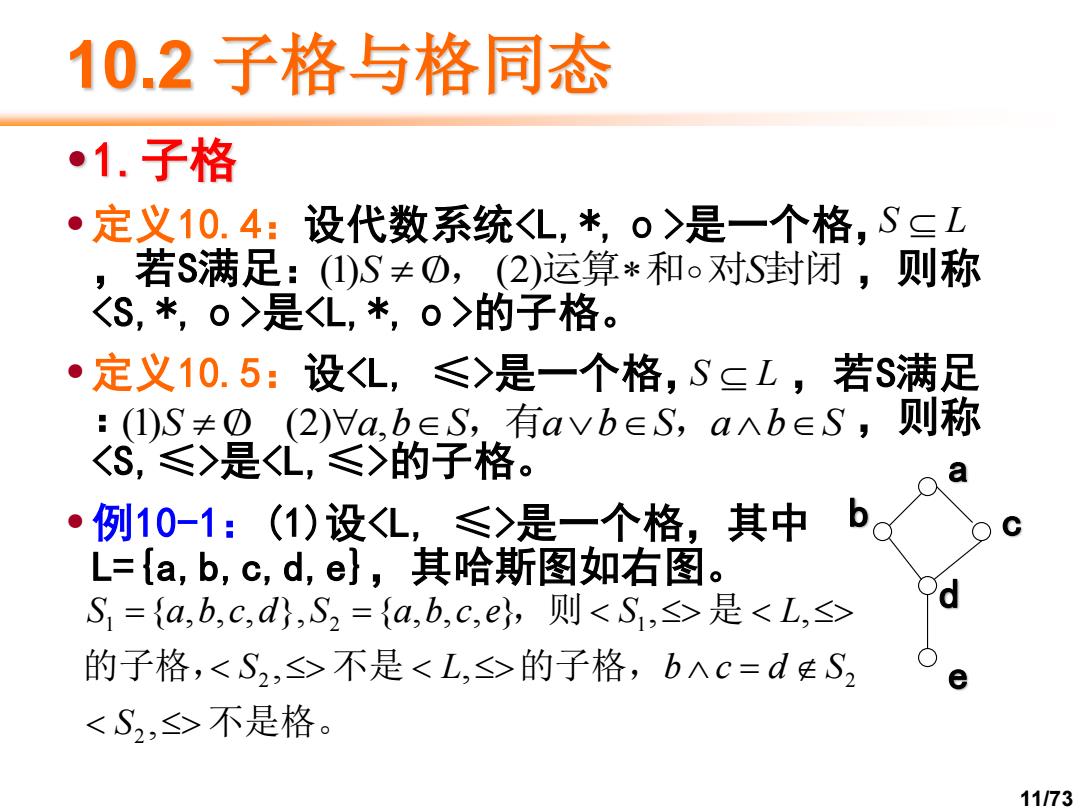
10.2子格与格同态 ·1.子格 ·定义10.4:设代数系统<L,*,o>是一个格,S二L ,若S满足:(①)S≠0,(2)运算*和。对S封闭,则称 <S,*,0>是<L,*,0>的子格。 ·定义10.5:设<L,≤>是一个格,S三L,若S满足 :(I)S≠①(2)a,b.∈S,.有avb∈S,aAb∈S,则称 S,≤>是<L,≤>的子格。 ●例10-1:(1)设<L,≤>是一个格,其中 L={a,b,c,d,e},其哈斯图如右图。 S1={a,b,c,d},S2={a,b,c,e,则<S1,>是<L,> 的子格,<S2,≤>不是<L,≤>的子格,bΛc=dS2 <S2,≤>不是格。 11/73
11/73 10.2 子格与格同态 •1.子格 •定义10.4:设代数系统<L,*,ο>是一个格, ,若S满足: ,则称 <S,*,ο>是<L,*,ο>的子格。 •定义10.5:设<L, ≤>是一个格, ,若S满足 : ,则称 <S,≤>是<L,≤>的子格。 •例10-1:(1)设<L, ≤>是一个格,其中 L={a,b,c,d,e},其哈斯图如右图。 S L (1)S , (2)运算和对S封闭 S L (1)S (2)a,bS,有abS,abS b a e c d 不是格。 的子格, 不是 的子格, ,则 是 = = = , , , { , , , } , { , , , } , , 2 2 2 1 2 1 S S L b c d S S a b c d S a b c e S L

10.2子格与格同态 ●2.格同态 定义10.6:设L和L,是格,0:L→L2,若a,beL 有p(aAb)=p(a)Ap(b),p(avb)=p(a)vp(b),则称p为 格L到L2的同态映射,简称格同态,若0是双射 ,则称0为格同构。 定义10.7:设L和L2是格,其中≤1,≤2分别为格L,L2 上的偏序关系,存在映射f:L→L,Va,b∈L 若a≤1b→f(a)≤2f(b),称f是序同态,若f是双射 则称f是序同构。 ● (格同态定理)定理10.4:(1)设0是格<L,≤>到 格<L,≤2>的同态,则p是序同态,即同态是保 序的,即x,y∈L,有x≤1y→p(x)≤2p(y) 12/73
12/73 10.2 子格与格同态 •2.格同态 •定义10.6:设 和 是格, ,若 有 ,则称 为 格 到 的同态映射,简称格同态,若 是双射 ,则称 为格同构。 •定义10.7:设 和 是格,其中 分别为格 上的偏序关系,存在映射 , 若 ,称f是序同态,若f是双射 ,则称f是序同构。 • (格同态定理)定理10.4:(1)设 是格 到 格 的同态,则 是序同态,即同态是保 序的,即 L1 L2 1 2 : L → L 1 a,bL (a b) =(a) (b),(a b) =(a)(b) L1 L2 L1 L2 1 2 , 1 2 L , L 1 2 1 f : L → L ,a,bL ( ) ( ) a 1 b f a 2 f b L1 ,1 L2 ,2 , ( ) ( ) 1 1 2 x yL,有x y x y

10.2子格与格同态 (2)0是双射,则P是<L,≤1>到<L2,≤2>的同构的充 要条件是x,y∈L,有x≤1y台p(x)≤2p(y) 证:(I):x,y∈L,x≤1y台xVy=y .p(y)=p(xVy)=p(x)Vp(y).p(x)≤2p(y)方 (2):(→油(I)得:x≤1y→p(x)≤2p(y),反之:p(x)≤2p(y) →p(x)Vp(y)=p(y)=p(xVy)→y=xVy→x≤1y (=)对Vx,y∈L,x≤1y台p(x)≤2p(y) 令xVy=z,则x≤12,y≤1z→p(x)≤2p(z),p(y)≤2p() ∴.p(x)Vp(y)≤0(z)=p(xVy) 另一方面,p是满射,p(x),p(y)∈L2,则p(x)Vp(y)∈L2 则必存在u∈L,使得p(u)=p(x)Vp(y) 13/73
13/73 10.2 子格与格同态 (2) 是双射,则 是 到 的同构的充 要条件是 L1 ,1 L2 ,2 , ( ) ( ) 1 1 2 x yL,有x y x y ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) , ( ) ( ) ( ) ( ) ( ) ( ) (2):( ) (1) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ); (1): , , 1 2 2 1 1 2 2 1 1 2 1 1 2 2 2 1 1 u L u x y x y L x y L x y z x y x y z x z y z x z y z x y L x y x y x y y x y y x y x y x y x y x y y x y x y x y x y L x y x y y = = = = = = = = = 则必存在 ,使得 另一方面, 是满射, , ,则 令 ,则 , , 对 , 由 得: ,反之: 证:
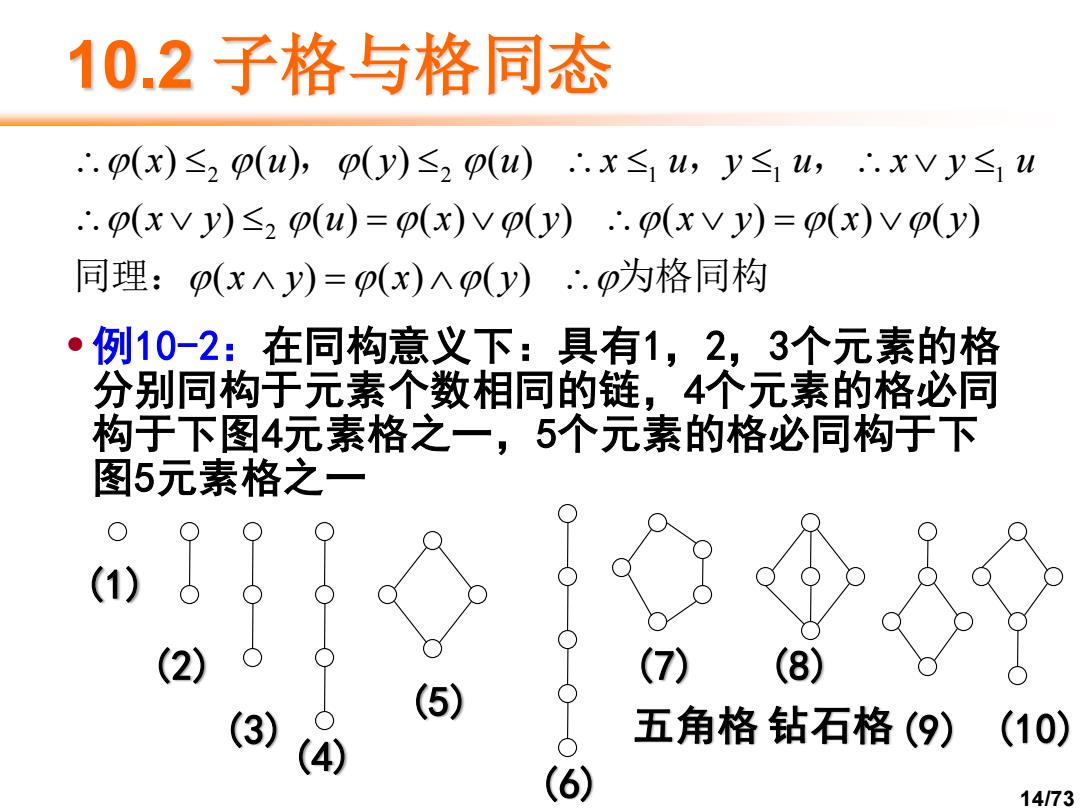
10.2子格与格同态 ∴.p(x)≤2p(u),p(y)≤2p(u).x≤1u,y≤1u,∴.xVy≤1u ..o(xvy)s2 o(u)=o(x)vo(y)..o(xvy)=o(x)vo(y) 同理:p(x入y)=p(x)Ap(y)∴p为格同构 例10-2:在同构意义下:具有1,2,3个元素的格 分别同构于元素个数相同的链,4个元素的格必同 构于下图4元素格之一,5个元素的格必同构于下 图5元素格之一 (2) (7) (5) 五角格钻石格(9)( 10) (4) (6) 14/73
14/73 10.2 子格与格同态 •例10-2:在同构意义下:具有1,2,3个元素的格 分别同构于元素个数相同的链,4个元素的格必同 构于下图4元素格之一,5个元素的格必同构于下 图5元素格之一 同理: 为格同构 , , , = = = ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 1 1 1 x y x y x y u x y x y x y x u y u x u y u x y u (2) (3)(4) (5) (6) (7) 五角格 (9) (8) 钻石格 (10) (1)