整个循环:O△U=0是体系所吸的热,为正值是体系放出的热,为负值0Q=0,+0P-W =Q, +QA(P,V,T,)W=Wi+W,+W3+WB(P2,V2, T)7W,和W对消D(P4,VT)C(P3,V3, T)T1VbdCa12
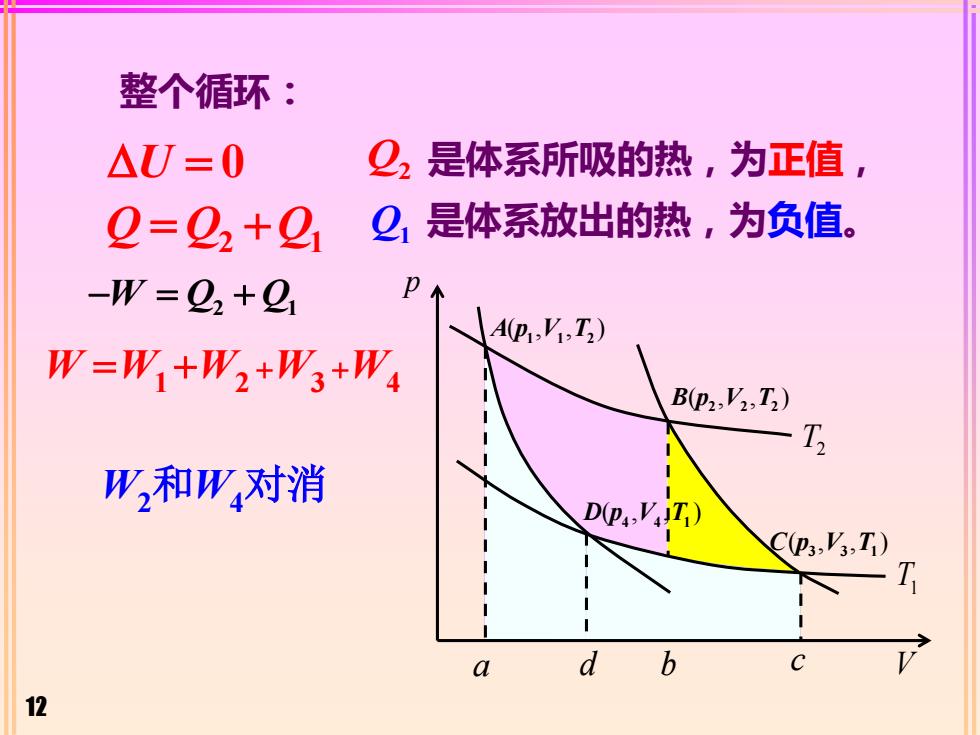
12 整个循环: = U 0 Q2 是体系所吸的热,为正值, Q1 是体系放出的热,为负值。 W W W W W 1 2 3 4 = + + + Q Q Q 2 1 = + W W 2 4 和 对消 p A p V T ( , , ) 1 1 2 B p V T ( , , ) 2 2 2C p V T ( , , ) 3 3 1 D p V T ( , , ) 4 4 1 V T2 T1 a d b c − = + W Q Q 2 1
ABCD曲线所围面整个循环:积为热机所作的功pA(p,V,T)B(p2,V2, T2)TD(p4,VAIT)C(p3, V3,T)- T1:1bdVca13
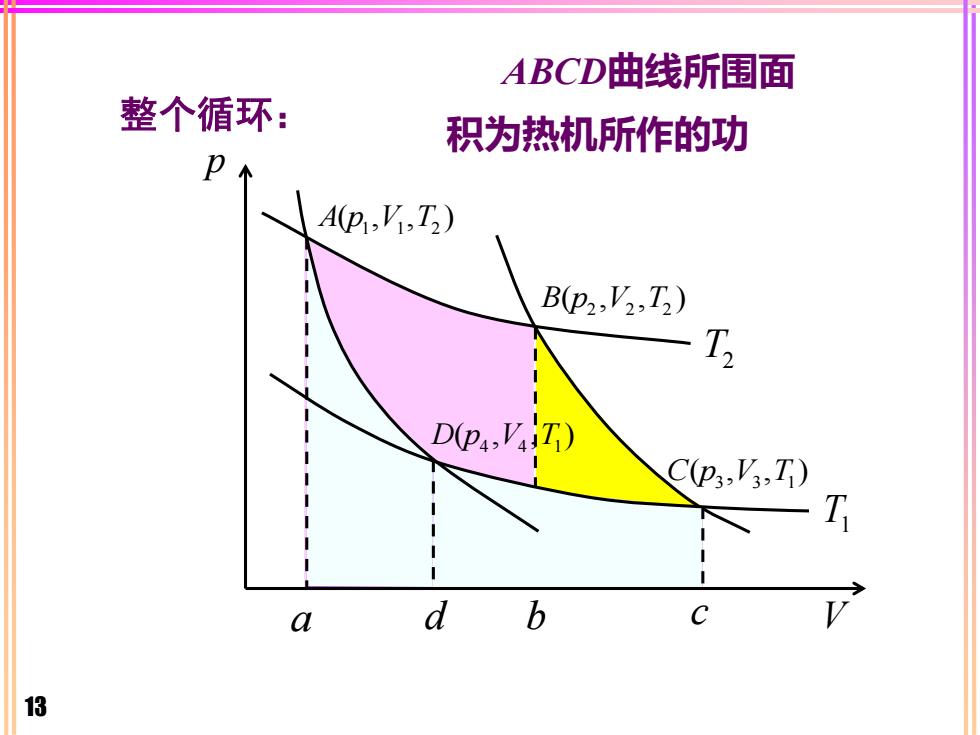
13 p 1 1 2 A p V T ( , , ) 2 2 2 B p V T ( , , ) 3 3 1 C p V T ( , , ) 4 4 1 D p V T ( , , ) V T2 T1 a d b c 整个循环: ABCD曲线所围面 积为热机所作的功
P根据绝热可逆过程方程式A(P,V,T,)B(P2,V2,T)T过程2:TV-' =TVr-!TD(P4,V过程4:TVr-I = TVI-!C(Ps,V,T)T1--V2VV相除得d6CaV.V4VL所以W +W =-nRT, InnRT In5V1V= nR(T, -T)InV14
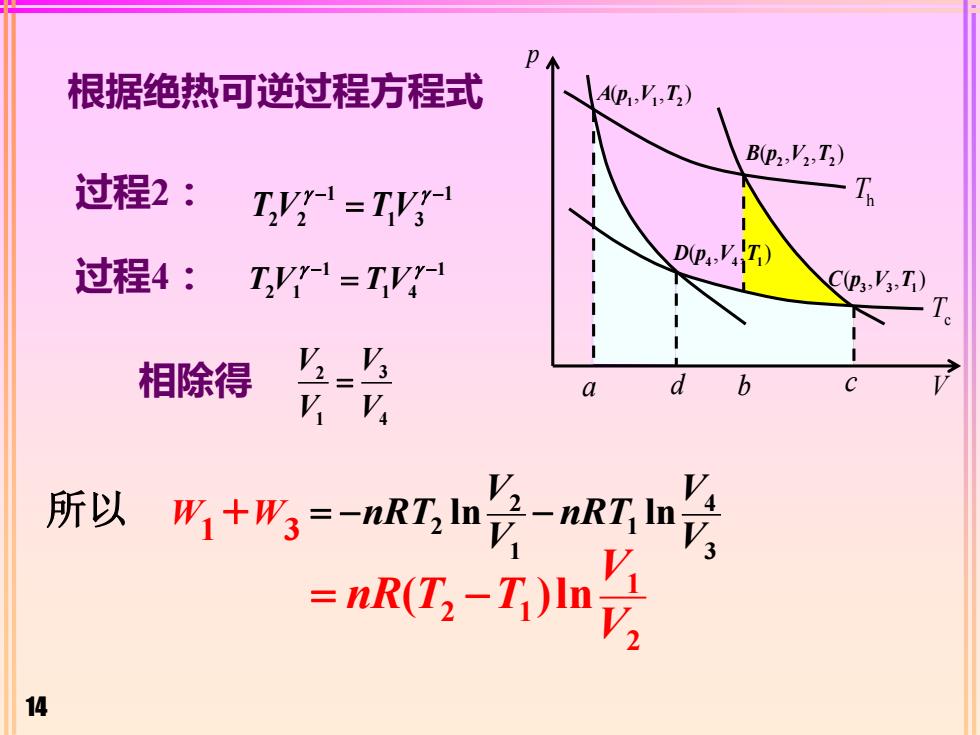
14 1 1 T V TV 2 2 1 3 − − 过程 = 2: 1 1 T V TV 2 1 1 4 − − 过程4: = V V V V 2 3 1 4 相除得 = 根据绝热可逆过程方程式 W W V V nRT nRT V V 2 4 2 1 1 3 1 3 所以 + = − − ln ln V nR T T V 1 2 1 2 = − ( )ln p A p V T ( , , ) 1 1 2 B p V T ( , , ) 2 2 2C p V T ( , , ) 3 3 1 D p V T ( , , ) 4 4 1 V Th Tc a d b c
2.热机效率将热机所作的功与所吸的热之比值称为热机效率,或称为热机转换系数,用n表示。-nR(T, - T)In(一-WT, -Tn==QT高温存储器T2-nRT, In()Q2T=1-WT热机或-WQ+Q191Q1(Q, <0):1+n=Q2Q2Q,T低温存储器n<1卡诺循环15
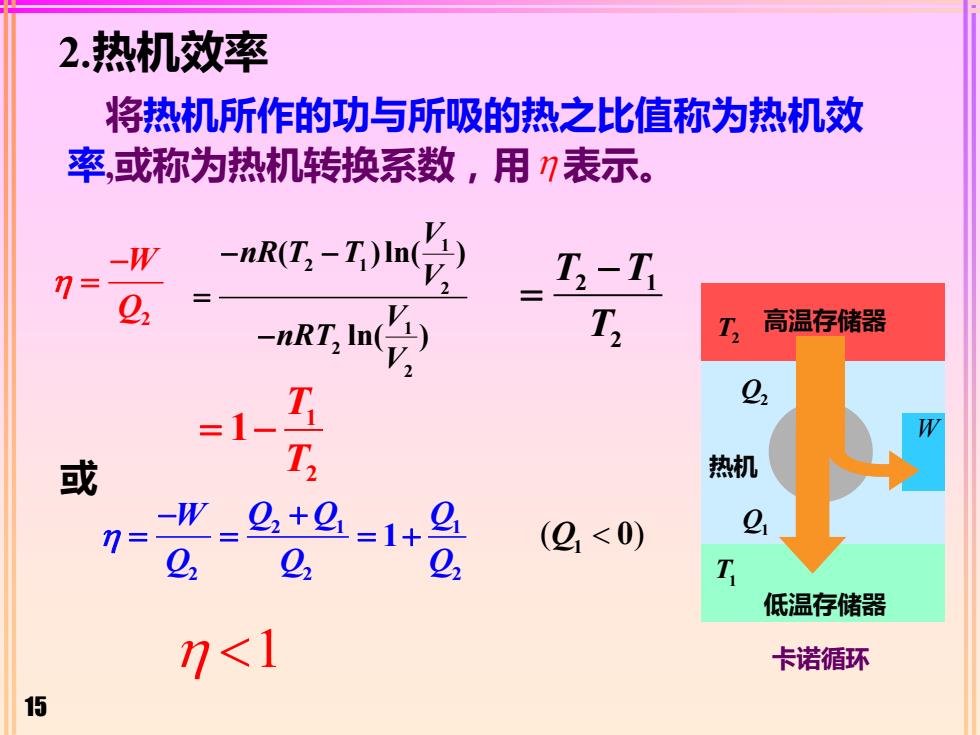
15 2.热机效率 将热机所作的功与所吸的热之比值称为热机效 率,或称为热机转换系数,用 表示。 1 W Q2 − = 或 T T 1 2 = −1 卡诺循环 高温存储器 低温存储器 热机 T2 W T1 Q2 W Q Q Q Q1 Q Q Q 2 1 1 2 2 2 1 − + = = = + ( ) Q1 0 V nR T T V V nRT V 1 2 1 2 1 2 2 ( )ln( ) ln( ) − − = − 2 1 2 T T T − =

3.卡诺定理:(1824年)1.在两个确定热源之间工作的所有热机中,卡诺热机效率最大;即T< ir cycle≤-nT2=rcycle意义:的极限提高的根本途径2.卡诺热机的效率只与热源温度有关,而与工作介质无关。neamot = 1 _ In=1-T2T16
16 3.卡诺定理:(1824年) 1.在两个确定热源之间工作的所有热机中,卡诺热机效 率最大;即 2.卡诺热机的效率只与热源温度有关,而与工作介质无 关。 2 1 1 T T − < ir cycle = r cycle 意义:的极限 提高的根本途径 2 1 r 1 T T = − 2 1 carnot 1 T T = −