$2.3卡诺循环和卡诺定理Carnot Cycle and Carnot Theorem卡诺热机:理想热机n(热机效率)=-W/Q2卡诺热机工作介质为理想气体,在T,T,=1+Q;/Q2两热源之间工作,经过一个由四个可逆过(W<0, Qi<0)程组成的循环过程一卡诺循环。A(P,V)高温热源TPT2B(P2,V)吸热Q2DT,C(p3,Vs)(P4,V)热机做出功WA→B:定温可逆膨胀,吸热Q2;放热QB→>C:绝热可逆膨胀:C→D:定温可逆压缩,放热Q;D→A:绝热可逆压缩:低温热源T7
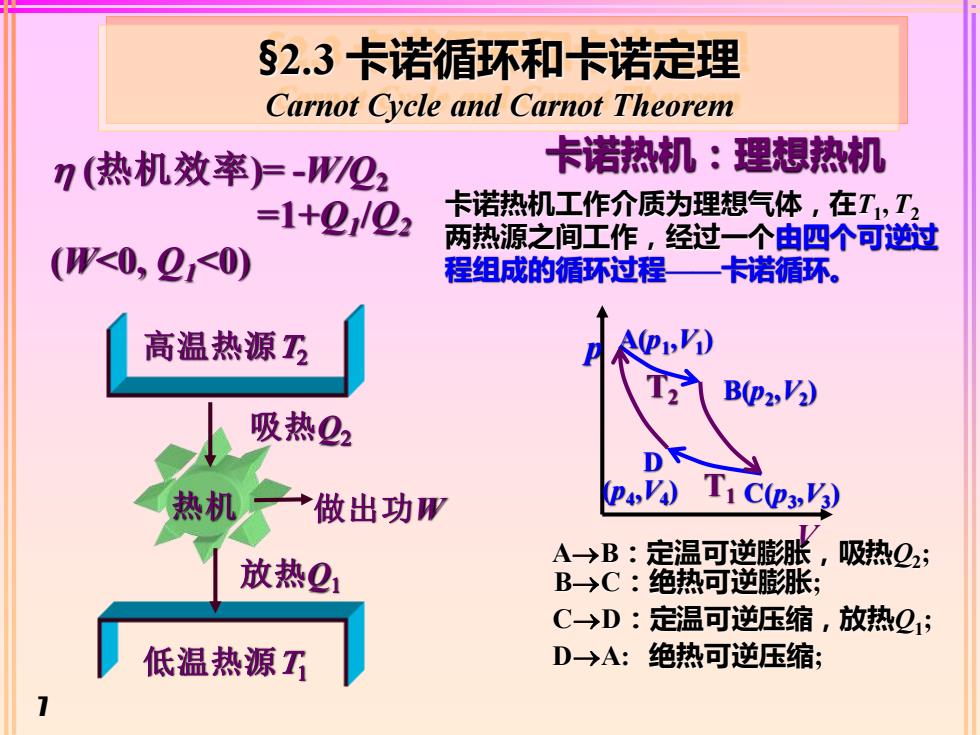
7 §2.3 卡诺循环和卡诺定理 Carnot Cycle and Carnot Theorem (热机效率)= -W/Q2 =1+Q1 /Q2 (W<0, Q1<0) 低温热源T1 高温热源T2 吸热Q2 放热Q1 做出功W 卡诺热机:理想热机 卡诺热机工作介质为理想气体,在T1 , T2 两热源之间工作,经过一个由四个可逆过 程组成的循环过程——卡诺循环。 p V A(p1 ,V1 ) B(p2 ,V2 ) T1 C(p3 ,V3 ) D (p4 ,V4 ) T2 B→C:绝热可逆膨胀; D→A: 绝热可逆压缩; A→B:定温可逆膨胀,吸热Q2 ; C→D:定温可逆压缩,放热Q1 ;
1.Carnot循环工作物质:1mol理想气体在p~V图上可以分为四步:过程1:等温可逆膨胀A(P1,Vi, T) → B(P2, V2,T2)△U, =0pA(PI,V,T)W = -nRT InB(P2,V2, T2)VTQ, = -W11系统所作功如AB曲11线下的面积所示ba8
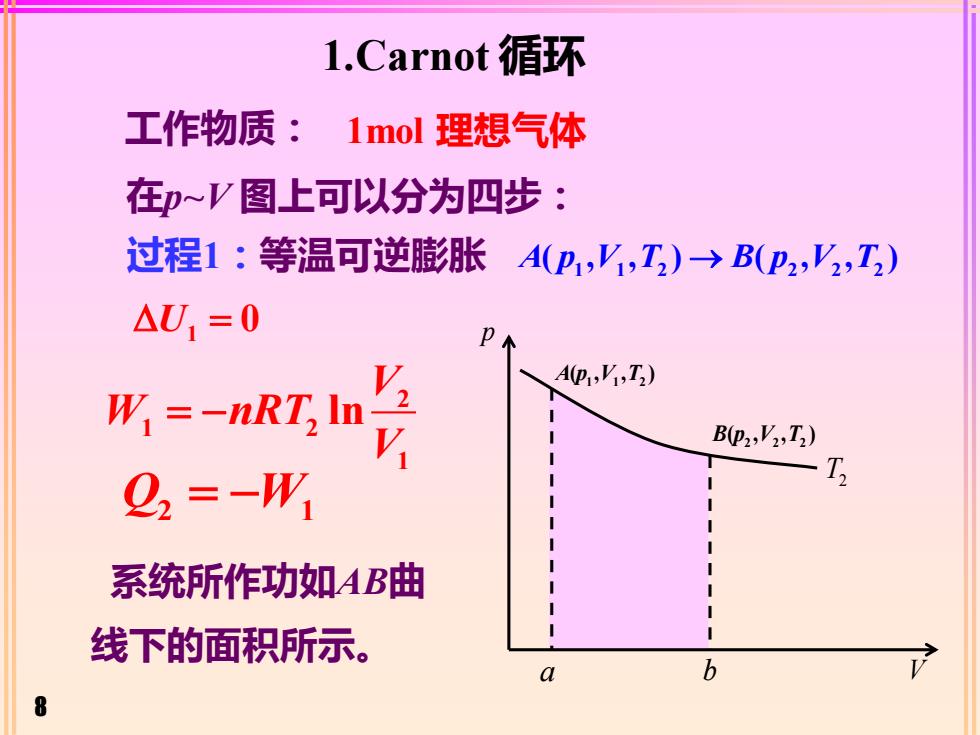
8 工作物质: 过程1:等温可逆膨胀 1 1 2 2 2 2 A p V T B p V T ( , , ) ( , , ) → 1 = U 0 2 1 2 1 lnV W nRT V = − 系统所作功如AB曲 线下的面积所示。 Q W 2 1 = − 1.Carnot 循环 在p~V 图上可以分为四步: 1mol 理想气体 p 1 1 2 A p V T ( , , ) 2 2 2 B p V T ( , , ) V T2 a b
过程2:绝热可逆膨胀B(P2, V2, T,) →C(P3, V3, T)=0QSA(Pi,Vi,T)W, = △UB(P2,V2,T,)TTCdTV.mT2C(P3,V3, T)系统所作功如BC曲L线下的面积所示bCa
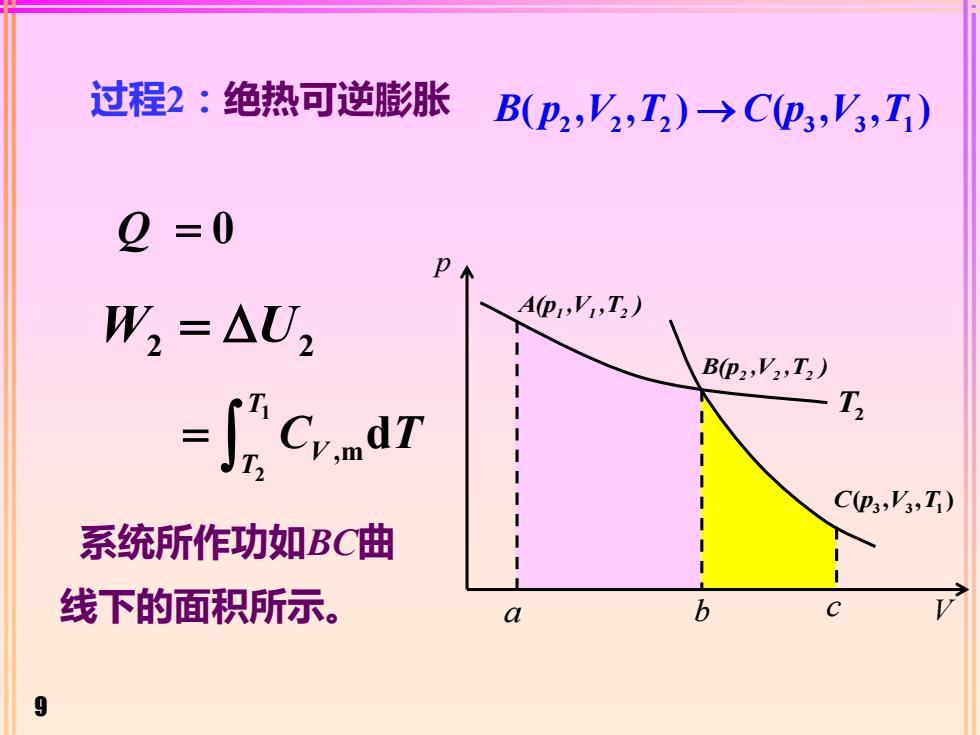
9 过程2:绝热可逆膨胀 2 2 2 3 3 1 B p V T C p V T ( , , ) ( , , ) → Q = 0 W U 2 2 = 系统所作功如BC曲 线下的面积所示。 1 2 ,md T V T = C T p A(p ,V ,T ) 1 1 2 B(p ,V ,T ) 2 2 2 3 3 1 C p V T ( , , )V T2 a b c
过程3:等温可逆压缩C(P3,V3,T) -→> D(P4,V4,T)△U, = 0pAA(Pi,VI,T)4W, =-nRT InB(P2,V2,T)4TO = -WD(PA,VT)TCP,-T1环境对系统所作功如1I1VbDC曲线下的面积所示Cda10
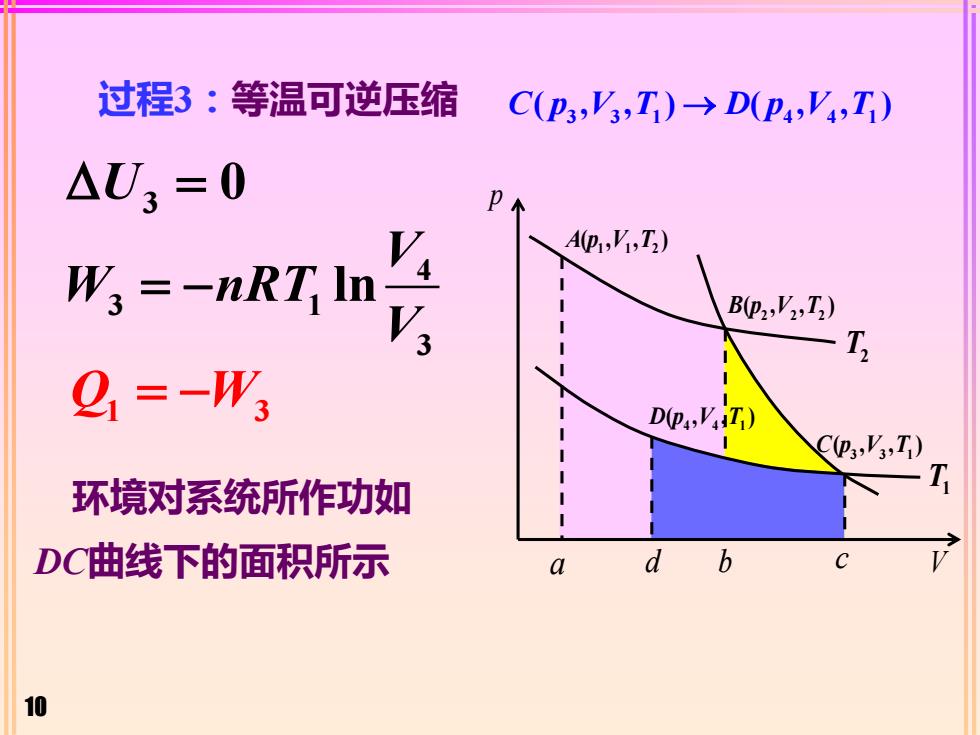
10 3 = U 0 环境对系统所作功如 DC曲线下的面积所示 Q W 1 3 = − 4 3 1 3 lnV W nRT V = − 过程3:等温可逆压缩 3 3 1 4 4 1 C p V T D p V T ( , , ) ( , , ) → p 1 1 2 A p V T ( , , ) 2 2 2 B p V T ( , , ) 3 3 1 C p V T ( , , ) 4 4 1 D p V T ( , , ) V T2 T1 a d b c
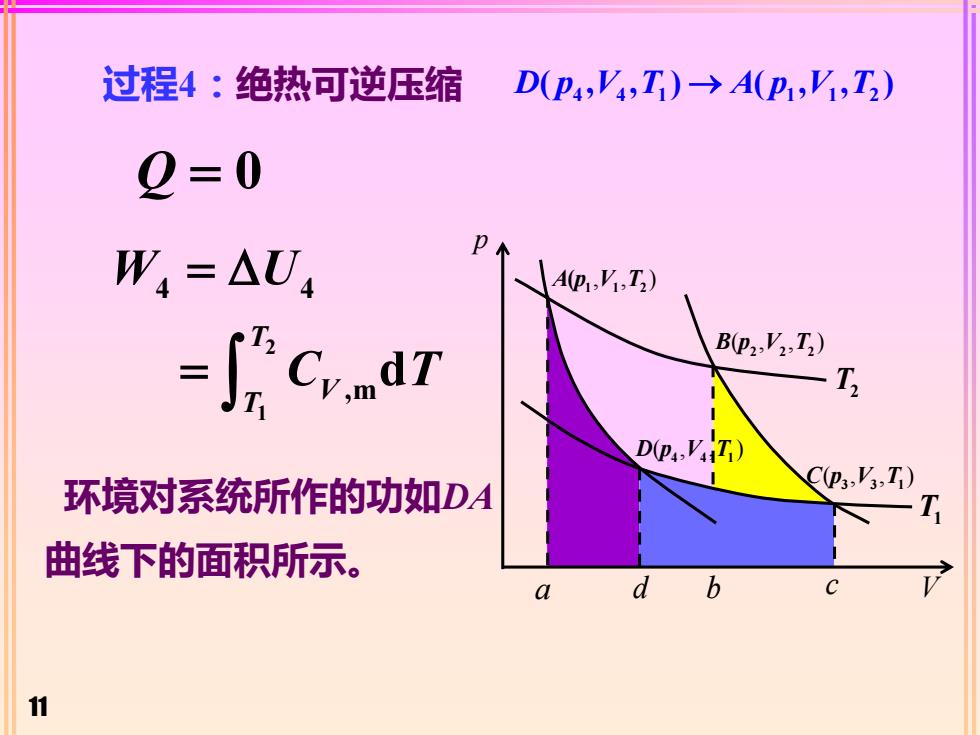
过程4:绝热可逆压缩D(P4,V4, T) -→ A(Pi,VI, T)Q=0pW = AUA(Pi,V,T,)T2B(P2,V2,T,)CdTTV,mT1D(P4,VA,T)(P3,V3,T环境对系统所作的功如DAT曲线下的面积所示VbdCa11
11 Q = 0 环境对系统所作的功如DA 曲线下的面积所示。 2 1 4 4 ,m d T V T W U C T = = 过程4:绝热可逆压缩 4 4 1 1 1 2 D p V T A p V T ( , , ) ( , , ) → p , , ) 1 1 2 A p V T ( ( , , ) B p V T 2 2 2 ( , , ) C p V T 3 3 1 ( , , ) D p V T 4 4 1 V T2 T1 a d b c