
余弦的乘积 [cos A=-cos BcosC+sin Bsin Ccosa cos B=-cos AcosC+sin Asin Ccosb (43.2) cosC=-cos Acos B+sin Asin Bcosc 公式(4.3.2)通常用于求解已知两角及其夹边求第三角或者已知三角求一边.它在航海 实际工作中比较少用. 4.3.2正弦公式 球面三角形各边的正弦和它对应角的正弦成正比 sina sinb sinc (4.3.3) sinA sin B sinC 公式(4.3.3)通常用于求解已知一边及其对角和另一边(角),求另一角(边).它在航 海实际工作中常用于求起航点与到达点之间的初始航向, 注:利用公式(4.3.3),所得到的解是两个互为补角的解,应根据实际问题来选择. 4.3.3边角的正余弦公式(五联公式) 球面三角形相邻边角正余弦的乘积等于邻边第三边正余弦的乘积减去邻边第三边余正 弦及其夹角余弦的乘积,即 sin边cos角=sin邻边cos第三边-cos邻边sin第三边cos夹角(口诀). (sin acos B=sin ccosb-coscsin bcos A sin acosC=sin bcosc-cosbsin ccos A sin bcos A=sin ccosa-coscsin acos B (4.3.40 sin bcosC=sin acosc-cosasin ccos B sin ccos A=sin bcosa-cosbsin acosC sin ccos B=sin acosb-cosasin bcosC 公式(4.3.4)通常用于推导其他的球面三角公式,一般不用于解球面三角形 注:五联公式的记忆,主要在于弄清邻边和第三边的概念 例如五个联起来的要素:a一B一c一A一b,称a为边,B为角,c为邻边,A为 夹角,b为第三边.套用口诀即可得到公式(43.4)中的第一个公式 4.3.4余切公式(四联公式) 球面三角形外边余切内边正弦的乘积等于外角余切内角正弦的乘积加上内边内角余弦 的乘积,即cot外边sin内边=cot外角sin内角+cos内边cos内角(口诀)
86 余弦的乘积. = − + = − + = − + C A B A B c B A C A C b A B C B C a cos cos cos sin sin cos cos cos cos sin sin cos cos cos cos sin sin cos (4.3.2) 公式(4.3.2)通常用于求解已知两角及其夹边求第三角或者已知三角求一边. 它在航海 实际工作中比较少用. 4.3.2 正弦公式 球面三角形各边的正弦和它对应角的正弦成正比. sin sin sin sin sin sin a b c A B C = = (4.3.3) 公式(4.3.3)通常用于求解已知一边及其对角和另一边(角),求另一角(边).它在航 海实际工作中常用于求起航点与到达点之间的初始航向. 注:利用公式(4.3.3),所得到的解是两个互为补角的解,应根据实际问题来选择. 4.3.3 边角的正余弦公式(五联公式) 球面三角形相邻边角正余弦的乘积等于邻边第三边正余弦的乘积减去邻边第三边余正 弦及其夹角余弦的乘积,即 sin 边 cos 角 = sin 邻边 cos 第三边 −cos 邻边 sin 第三边 cos 夹角 (口诀). = − = − = − = − = − = − c B a b a b C c A b a b a C b C a c a c B b A c a c a B a C b c b c A a B c b c b A sin cos sin cos cos sin cos sin cos sin cos cos sin cos sin cos sin cos cos sin cos sin cos sin cos cos sin cos sin cos sin cos cos sin cos sin cos sin cos cos sin cos (4.3.4) 公式(4.3.4)通常用于推导其他的球面三角公式,一般不用于解球面三角形. 注:五联公式的记忆,主要在于弄清邻边和第三边的概念. 例如五个联起来的要素: a- B -c - A -b ,称 a 为边, B 为角, c 为邻边, A 为 夹角, b 为第三边. 套用口诀即可得到公式(4.3.4)中的第一个公式. 4.3.4 余切公式(四联公式) 球面三角形外边余切内边正弦的乘积等于外角余切内角正弦的乘积加上内边内角余弦 的乘积,即 cot 外边 sin 内边 = cot 外角 sin 内角 +cos 内边 cos 内角(口诀)

[cot asin b=cot Asin C+cosbcosC cotasin c=cot Asin B+cosccos B cot bsin a=cot Bsin C+cosacosC (4.3.5) cotbsin c cot Bsin A+cosccosA cotcsin a=cotCsin B+cosacos B cotcsin b=cotCsin A+cosbcos A 公式(4.35)通常用于求四个联起来要素中的外边或者外角。它在航海实际工作中是常 用的公式之一,如求起航点与到达点之间的初始航向。 注:四联公式的记忆,主要在于弄清内(外)边和内(外)角的概念 例如四个联起来的要素:a一C一b一A,称a为外边,b为内边,A为外角,C为 内角.套用口诀即可得到公式(4.3.5)中的第一个公式. 例1在球面三角形ABC中,已知A=a,求证:B与b、C与c相等或互补. 证明因为m4-smb。s咖c sin sin B sin C 1,所以,sinB=sinb,snC=sinc: 即B与b、C与c相等或互补. 例2球面三角形各边都等于60°,求证每个角的余弦为 解由边的余弦公式:cosa=cosbcosc+-sinbsinccosA,得 c0sA=cosa-cosbc0se-cos60°-c0s60°cos60° sin bsin c sin60°sin60° 3:同理可证 练习题4.3 1.在球面三角形ABC中,若C=90,求证:(1)cosc=cosacosb: (2)cosc=cot Acot B:(3)sin b=cot Atana:(4)sin b=sin Bsinc 2。球面三角形各角都等于120°,求证每个边的余弦为-了 3.在周长为12的球面上,一个球面三角形ABC的三边长分别为AB=1,BC=2, AC=求它的三个内角 4.如图4.3.1,在球面三角形ABC中,D是AB上的 中点,过C、D两点作大圆弧CD,CD分角C为x、 B y两个部分.求证: sinx sinb siny sina' 图4.3
87 = + = + = + = + = + = + c b C A b A c a C B a B b c B A c A b a B C a C a c A B c B a b A C b C cot sin cot sin cos cos cot sin cot sin cos cos cot sin cot sin cos cos cot sin cot sin cos cos cot sin cot sin cos cos cot sin cot sin cos cos (4.3.5) 公式(4.3.5)通常用于求四个联起来要素中的外边或者外角. 它在航海实际工作中是常 用的公式之一,如求起航点与到达点之间的初始航向. 注:四联公式的记忆,主要在于弄清内(外)边和内(外)角的概念. 例如四个联起来的要素: a-C -b - A ,称 a 为外边, b 为内边, A 为外角, C 为 内角. 套用口诀即可得到公式(4.3.5)中的第一个公式. 例 1 在球面三角形 ABC 中,已知 A a = ,求证: B 与 b 、C 与 c 相等或互补. 证明 因为 1 sin sin sin sin sin sin = = = C c B b A a ,所以, sin B = sin b,sin C = sin c ; 即 B 与 b 、C 与 c 相等或互补. 例 2 球面三角形各边都等于 0 60 ,求证每个角的余弦为 1 3 . 解 由边的余弦公式:cos cos cos sin sin cos a b c b c A = + ,得 = − = b c a b c A sin sin cos cos cos cos 0 0 0 0 0 cos60 cos60 cos60 1 sin 60 sin 60 3 − = ;同理可证. 练习题 4.3 1.在球面三角形 ABC 中,若 0 C = 90 ,求证:(1) cos cos cos c a b = ; (2) cosc = cot Acot B ;(3) sin b = cot Atan a ;(4) sin b = sin Bsin c . 2.球面三角形各角都等于 0 120 ,求证每个边的余弦为 1 3 − . 3. 在周长为 12 的球面上,一个球面三角形 ABC 的三边长分别为 AB =1, BC = 2 , 3 2 AC = ,求它的三个内角. 4. 如图 4.3.1,在球面三角形 ABC 中, D 是 AB 上的 中点,过 C 、 D 两点作大圆弧 CD,CD 分角 C 为 x 、 y 两个部分. 求证: sin sin sin sin x b y a = . 图 4.3.1
5.设C=90°,a=60°,b=45°,求:(1)边c:(2)角A 4.4球面直角三角形和球面直边三角形 4.4.1球面直角三角形 1、定义至少有一个角为直角的球面三角形称为球面直角三角形. 若三个角都是90°,则三边也都是90°;若两个角是90°,则直角的两对边也是90°, 此时第三个角所对应的顶点和对边是极点和极线的关系,由球面角的知识,第三个角与其对 边在数值上必相等(同度),所以上述两种情况下球面三角形的边角关系已经很清楚,下面 仅讨论一个角为直角的球面三角形的公式 2、球面直角三角形公式推导 设C=90°,则有snC=1,c0sC=0,对照边的余弦公式、角的余弦公式、正弦公 式、余切公式可推得下表的10个公式. 表4.4.1 公式名称 球面任意三角形 球面直角三角形(C=90° 边的余弦公式 cosc=cos acosb+sin asin bcosC cosc=cosacosb 角的余弦公式 cos A=-cos BcosC+sin Bsin Ccosa cos A=sin Bcosa cos B=-cos AcosC+sin Asin Ccosb cos B=sin Acosb cosC=-cos Acos B+sin Asin Bcosc cosc=cot Acot B 正弦公式 sin a sin c sin a=sin Asinc sin 4 sin C sin b sin c sinb=sin Bsin c snBsnG 余切公式 cot asin b=cot Asin C+cosbcosC sin b=cot Atana cot bsin a=cot Bsin C+cosacosC sin a=cot Btan b cotcsin a=cotCsin B+cosacos B cos B=tanacotc cotcsin b=cotCsin A+cosbcosA cosA=tanbcotc 由此我们得到了这十个公式,这十个公式包括了球面直角三角形在角C=90°时的所有 情况,即:
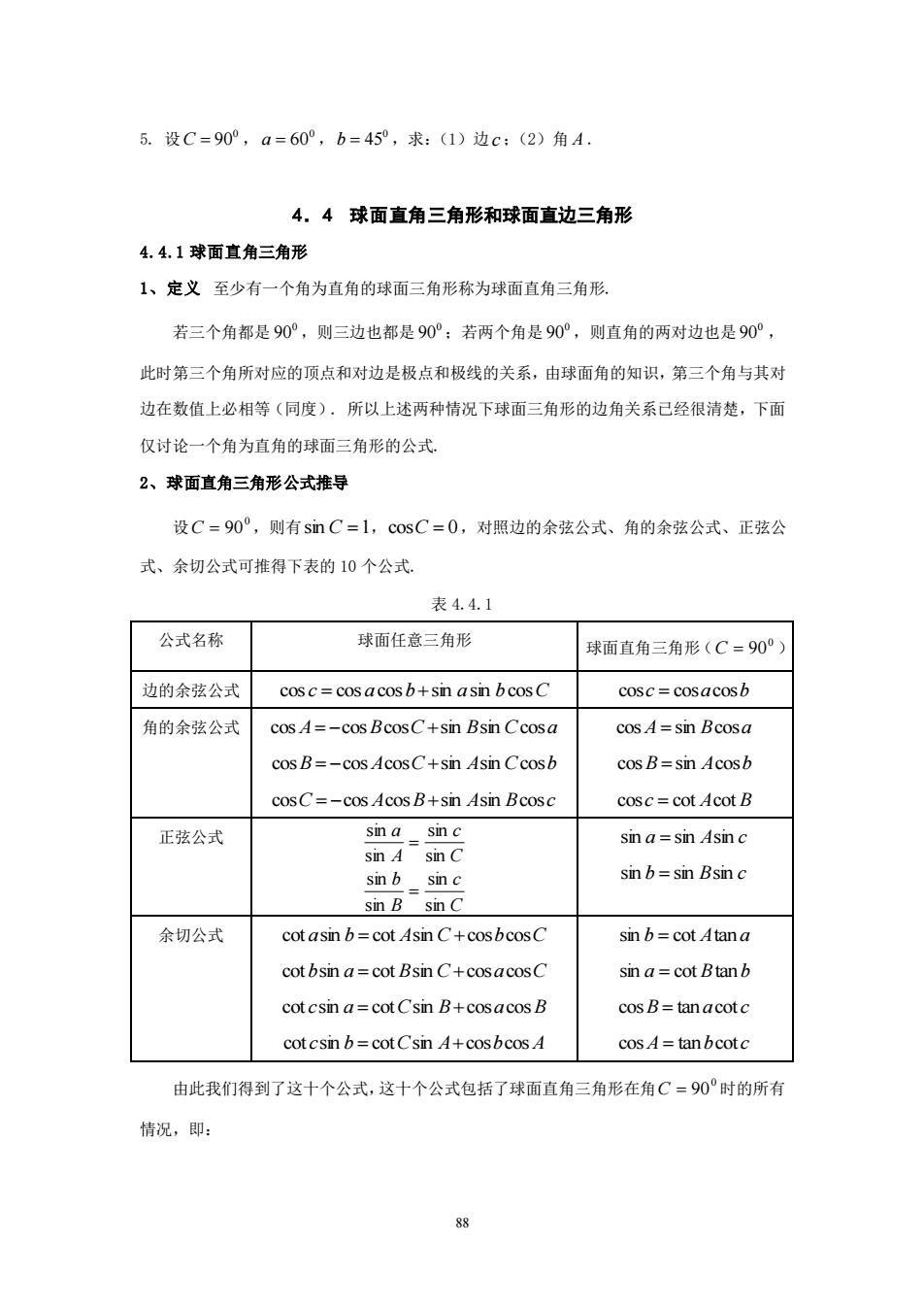
88 5. 设 0 C = 90 , 0 a = 60 , 0 b = 45 ,求:(1)边 c ;(2)角 A . 4.4 球面直角三角形和球面直边三角形 4.4.1 球面直角三角形 1、定义 至少有一个角为直角的球面三角形称为球面直角三角形. 若三个角都是 0 90 ,则三边也都是 0 90 ;若两个角是 0 90 ,则直角的两对边也是 0 90 , 此时第三个角所对应的顶点和对边是极点和极线的关系,由球面角的知识,第三个角与其对 边在数值上必相等(同度). 所以上述两种情况下球面三角形的边角关系已经很清楚,下面 仅讨论一个角为直角的球面三角形的公式. 2、球面直角三角形公式推导 设 0 C = 90 ,则有 sin C =1,cosC = 0 ,对照边的余弦公式、角的余弦公式、正弦公 式、余切公式可推得下表的 10 个公式. 表 4.4.1 公式名称 球面任意三角形 球面直角三角形( 0 C = 90 ) 边的余弦公式 cos c = cos a cosb+sin asin bcosC cosc = cosacosb 角的余弦公式 cos A= −cosBcosC+sin Bsin Ccosa cosB = −cos AcosC+sin Asin Ccosb cosC = −cos AcosB+sin Asin Bcosc cos A = sin Bcosa cosB = sin Acosb cosc = cot Acot B 正弦公式 C c A a sin sin sin sin = C c B b sin sin sin sin = sin a = sin Asin c sin b = sin Bsin c 余切公式 cot asin b = cot Asin C+cosbcosC cotbsin a = cot Bsin C+cosacosC cot csin a = cotCsin B+cosacosB cot csin b = cotCsin A+cosbcos A sin b = cot Atan a sin a = cot Btanb cosB = tan acot c cos A = tanbcot c 由此我们得到了这十个公式,这十个公式包括了球面直角三角形在角 0 C = 90 时的所有 情况,即:

cosc=cot Acot B=cosacosb sin a=sin Asin c=cot Btanb sin b=cot Atan a=sin Bsin c (4.4.1) cosA=tan bcotc=sin Bcosa cos B=tan acotc=sin Acosb 注:公式(4.4.1)仅适用于C=90°.若是A-90°或是B=90°,请参照上表的推导方法 将相应的字母改换即可. 3、球面直角三角形公式的记忆法则(纳比尔法则) 这十个球面直角三角形公式在实用中难于记忆,因此,纳比尔设计了一套图形(图 44.1)和记忆法则,用于记忆这些公式,称为纳比尔法则. C=90 90°- /90°、 图4.4.1 纳比尔法则:在非直角的五个循环要素中,任一要素的正弦,等于其相邻两要素正切的 乘积,或等于其相隔两要素余弦的乘积。纳比尔法则又称为“大字法则”。 在直角的情况下,任意己知两个要素,运用法则,可以直接求出其余三个要素。 注:1、大字图形下方的三个要素是90°-?: 2、法则中的五个循环要素不包括直角要素。 4.4.2球面直边三角形 1、定义至少有一个边为90°的球面三角形称为球面直边三角形. 若三条边都是90°,则三角也都是90°:若两条边是90°,则直边的两对角都是90°,而 第三条边与其角在数值上必相等.因此上述两种情况下球面三角形的边角关系己经很清楚, 下面仅讨论一条边为直边的球面三角形公式, 2、球面直边三角形公式 设c=90”,类似于球面直角三角形公式的推导,由边的余弦公式、角的余弦公式、正 弦公式、余切公式可推得10个公式.即
89 = = = = = = = = = = B a c A b A b c B a b A a B c a A c B b c A B a b cos tan cot sin cos cos tan cot sin cos sin cot tan sin sin sin sin sin cot tan cos cot cot cos cos (4.4.1) 注:公式(4.4.1)仅适用于 0 C = 90 . 若是 0 A = 90 或是 0 B = 90 ,请参照上表的推导方法, 将相应的字母改换即可. 3、球面直角三角形公式的记忆法则(纳比尔法则) 这十个球面直角三角形公式在实用中难于记忆,因此,纳比尔设计了一套图形(图 4.4.1)和记忆法则,用于记忆这些公式,称为纳比尔法则. 图 4.4.1 纳比尔法则:在非直角的五个循环要素中,任一要素的正弦,等于其相邻两要素正切的 乘积,或等于其相隔两要素余弦的乘积. 纳比尔法则又称为“大字法则”. 在直角的情况下,任意已知两个要素,运用法则,可以直接求出其余三个要素. 注:1、大字图形下方的三个要素是 90 ? 0 − ; 2、法则中的五个循环要素不包括直角要素. 4.4.2 球面直边三角形 1、定义 至少有一个边为 0 90 的球面三角形称为球面直边三角形. 若三条边都是 0 90 ,则三角也都是 0 90 ;若两条边是 0 90 ,则直边的两对角都是 0 90 ,而 第三条边与其角在数值上必相等. 因此上述两种情况下球面三角形的边角关系已经很清楚, 下面仅讨论一条边为直边的球面三角形公式. 2、球面直边三角形公式 设 0 c = 90 ,类似于球面直角三角形公式的推导,由边的余弦公式、角的余弦公式、正 弦公式、余切公式可推得 10 个公式. 即 0 90 0 C = 90a 0 90 − c 0 0 90 − B 90 − A b b a c C

cosC=-cotacot b=-cos Acos B sin A=cotbtan B=sin asin C sin B=cotatan A=sin bsin C (4.4.2) cosa=-cotCtan B=sin bcosA cosb=-cotCtan A=sin acos B 3、球面直边三角形公式的记亿法则 c=90 c=900 B 900-h 90°-a /90°-C 图4.4.2 与球面直角三角形公式类似,球面直边三角形公式也有纳比尔法则. 纳比尔法则:在五个循环要素中,任一要素的正弦,等于其相邻两要素正切的乘积,或 等于其相隔两要素余弦的乘积。但在等式右边的两项的乘积中,若两个要素都是边或都是角 时,则在乘积之前冠以负号. 在直边的情况下,任意己知两个要素,运用法则,可以直接求出其余三个要素,但是要 注意符号 例在球面三角形ABC中,设B=90°,则cosB=-cosAcosC或cot Acota 练习题4.4 1.在球面角形ABC中,设B=90°,则cOsb= 或 2.在球面三角形ABC中,设a=90°,则c0sA=_ 或 3.在球面三角形ABC中,边b=90°,a=60°,C=30°,求出其余的三要素 4.球面三角形ABC中,边a=90°,B=30°,C=45°,求出其余的三要素 5.球面三角形ABC中,C=90°,求证: (1)tanacosc=-sinbcot B:(2)sin2A=1-sin2 Bcos'a
90 = − = = − = = = = = = − = − b C A a B a C B b A B a A b C A b B a C C a b A B cos cot tan sin cos cos cot tan sin cos sin cot tan sin sin sin cot tan sin sin cos cot cot cos cos (4.4.2) 3、球面直边三角形公式的记忆法则 图 4.4.2 与球面直角三角形公式类似,球面直边三角形公式也有纳比尔法则. 纳比尔法则:在五个循环要素中,任一要素的正弦,等于其相邻两要素正切的乘积,或 等于其相隔两要素余弦的乘积. 但在等式右边的两项的乘积中,若两个要素都是边或都是角 时,则在乘积之前冠以负号. 在直边的情况下,任意已知两个要素,运用法则,可以直接求出其余三个要素,但是要 注意符号. 例 在球面三角形 ABC 中,设 0 B = 90 ,则 cosB = −cos cos A C 或 cot cot A a . 练习题 4.4 1.在球面三角形 ABC 中,设 0 B = 90 ,则 cosb = 或 . 2.在球面三角形 ABC 中,设 0 a = 90 ,则 cos A= 或 . 3.在球面三角形 ABC 中,边 0 b = 90 , 0 a = 60 , 0 C = 30 ,求出其余的三要素. 4.球面三角形 ABC 中,边 0 a = 90 , 0 B = 30 , 0 C = 45 ,求出其余的三要素. 5. 球面三角形 ABC 中, 0 C = 90 ,求证: (1) tan cos sin cot a c b B = − ;(2) 2 2 2 sin 1 sin cos A B a = − . 0 90 −C 0 c = 90A 0 0 90 −b 90 − a B A B 0 c = 90C