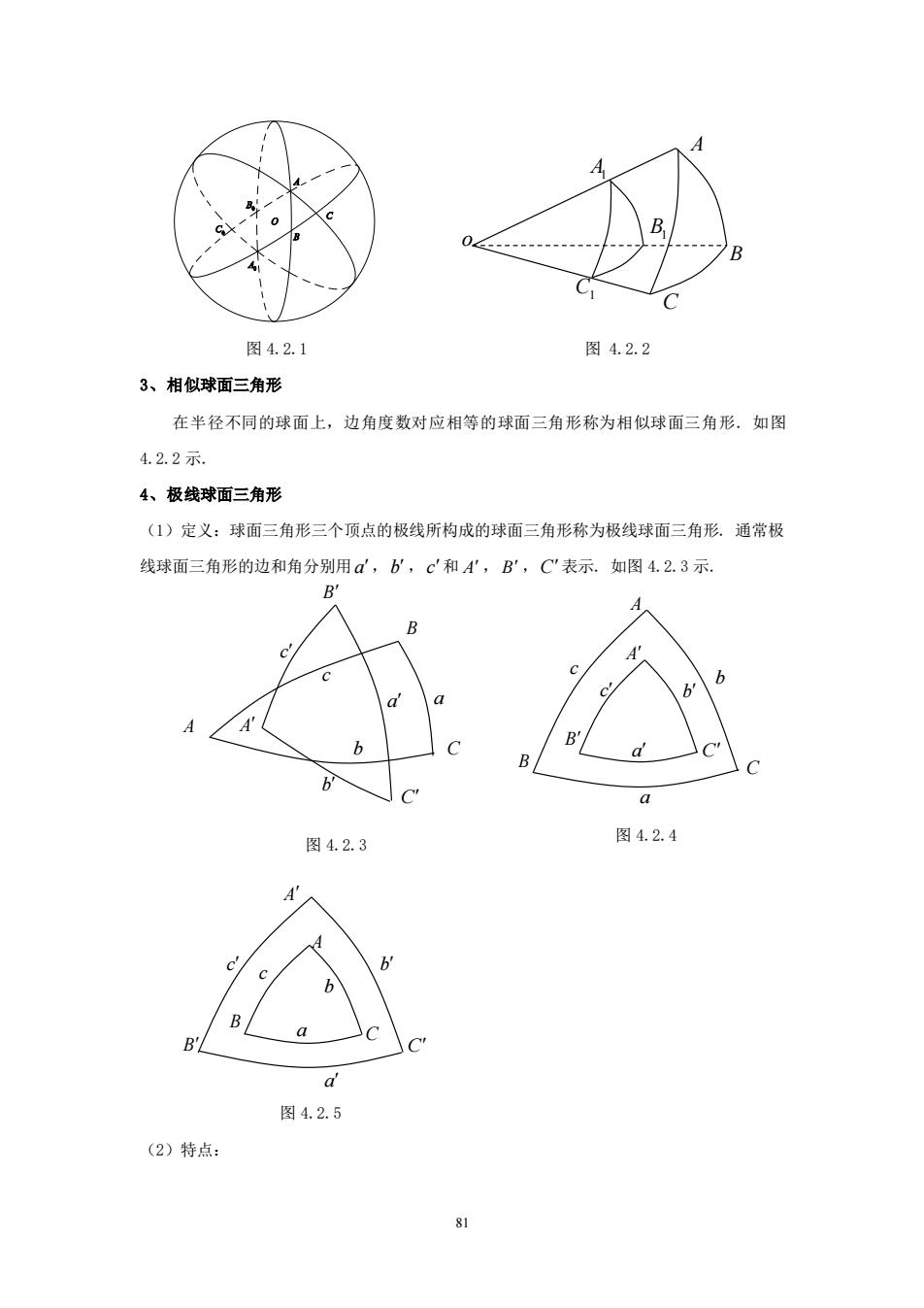
图4.2.1 图4.2.2 3、相似球面三角形 在半径不同的球面上,边角度数对应相等的球面三角形称为相似球面三角形.如图 4.2.2示. 4、极线球面三角形 (1)定义:球面三角形三个顶点的极线所构成的球面三角形称为极线球面三角形.通常极 线球面三角形的边和角分别用d,b,c'和A',B',C表示.如图42.3示. 图4.2.3 图4.2.4 图4.2.5 (2)特点:
81 图 4.2.1 图 4.2.2 3、相似球面三角形 在半径不同的球面上,边角度数对应相等的球面三角形称为相似球面三角形. 如图 4.2.2 示. 4、极线球面三角形 (1)定义:球面三角形三个顶点的极线所构成的球面三角形称为极线球面三角形. 通常极 线球面三角形的边和角分别用 a ,b ,c 和 A , B ,C 表示. 如图 4.2.3 示. (2)特点: o A B1 C1 A1 B C A B C A B C 图 4.2.4 a c b b a c A B C A B C 图 4.2.5 a a b c b c A A B B C C 图 4.2.3 c c b b a a

①若原球面三角形的三边都大于90°,则极线球面三角形在原球面三角形内:如图4.2.4示 ②若原球面三角形的三边都小于90°,则极线球面三角形在原球面三角形外:如图4.2.5示 ③若原球面三角形的一边或两边大于90°,则极线球面三角形与原球面三角形交叉形成。如 图4.2.3示. (3)关系: ①原球面三角形与极线球面三角形是相互的关系,即原球面三角形的顶点是极线球面三角形 对应边的极:反之,极线球面三角形的顶点是原球面三角形对应边的极。 ②原三角形的角(边)与极线球面三角形的边(角)互补.即 a+=180°,d+A=180°, b+B=180°,b+B=180°, c+C'=180°,c+C=180° 注:全等球面三角形与平面三角形全等的条件一样 4.2.4球面三角形的性质 1、球面三角形与三面角的关系 球面三角形与三面角之间可以相互度量,有如下的关系。如图4.2.6示 (1)球心是三面角的顶点: (2)球半径是三面角的棱: (3)球面三角形的边是三面角的平面角: (4)球面三角形的角是三面角的二面角, 02 2、球面三角形的边 (1)三边都是大圆弧,且0°<每一边<180° 图4.2.6 (2)两边之和大于第三边,两边之差小于第三边,如a-b<c<a+: (3)三边之和大于0°且小于360°,即0°<a+b+c<360°. 3、球面三角形的角 (1)0°<每-一角<180° (2)三角之和大于180°小于540°,即180°<A+B+C<540°
82 ①若原球面三角形的三边都大于 0 90 ,则极线球面三角形在原球面三角形内;如图 4.2.4 示. ②若原球面三角形的三边都小于 0 90 ,则极线球面三角形在原球面三角形外;如图 4.2.5 示. ③若原球面三角形的一边或两边大于 0 90 ,则极线球面三角形与原球面三角形交叉形成. 如 图 4.2.3 示. (3)关系: ①原球面三角形与极线球面三角形是相互的关系,即原球面三角形的顶点是极线球面三角形 对应边的极;反之,极线球面三角形的顶点是原球面三角形对应边的极. ②原三角形的角(边)与极线球面三角形的边(角)互补. 即 0 a A + = 180 , 0 a A + =180 , 0 b B+ = 180 , 0 b B + =180 , 0 c C+ = 180 , 0 c C + =180 . 注:全等球面三角形与平面三角形全等的条件一样. 4.2.4 球面三角形的性质 1、球面三角形与三面角的关系 球面三角形与三面角之间可以相互度量,有如下的关系. 如图 4.2.6 示. (1)球心是三面角的顶点; (2)球半径是三面角的棱; (3)球面三角形的边是三面角的平面角; (4)球面三角形的角是三面角的二面角. 2、球面三角形的边 (1)三边都是大圆弧,且 0 0 < 每一边 0 <180 ; (2)两边之和大于第三边,两边之差小于第三边,如 a −b c a +b ; (3)三边之和大于 0 0 且小于 0 360 ,即 0 0 0 < <360 abc + + . 3、球面三角形的角 (1) 0 0 < 每一角 0 <180 ; (2))三角之和大于 0 180 小于 0 540 ,即 0 0 180 < <540 A B C + + ; o A B1 C1 A1 B C 图 4.2.6 b c a

(3)两角之和减去第三角小于180°,如A+B-C<180°: (4)两角之和(差)大于(小于)第三角的外角,如A-B<D<A+B,如图4.2.7示. 4、边与角 A (1)等边对等角,等角对等边: (2)大(小)边对大(小)角,大(小)角对大(小) 边. 4.2.5球面三角形成立的条件 1、已知球面三角形的三个边时: (1)0°<每一边<180°: 图4.2.7 (2)0°<a+b+c<360°: (3)两边之和大于第三边,两边之差小于第三边. 2、已知球面三角形的三个角时: (1)0°<每一角<180°: (2)180°<A+B+C<540°: (3)两角之和减去第三角小于180° 3、若给定球面三角形的两个角(边)及其夹边(角),则仅需满足每一个角和每一个边大于 0°,小于180°的条件,球面三角形都成立 注:c边和C角在写法上的区别. 例判断下面的球面三角形是否存在. 1.A=100°,B=170°,C=70° 解:A+B-C=200°>180°,球面三角形不存在。 2.a=100°,b=170°,c=70°. 解a+c-170°-b,球面三角形不存在 3.A=100°,B=100°,C=100° 解满足已知三角的三个条件,“球面三角形存在
83 (3)两角之和减去第三角小于 0 180 ,如 0 A B C + − 180 ; (4)两角之和(差)大于(小于)第三角的外角,如 A − B D A + B . 如图 4.2.7 示. 4、边与角 (1)等边对等角,等角对等边; (2)大(小)边对大(小)角,大(小)角对大(小) 边. 4.2.5 球面三角形成立的条件 1、已知球面三角形的三个边时: (1) 0 0 < 每一边 0 <180 ; (2) 0 0 0 < <360 abc + + ; (3)两边之和大于第三边,两边之差小于第三边. 2、已知球面三角形的三个角时: (1) 0 0 < 每一角 0 <180 ; (2) 0 0 180 < <540 A B C + + ; (3)两角之和减去第三角小于 0 180 . 3、若给定球面三角形的两个角(边)及其夹边(角),则仅需满足每一个角和每一个边大于 0 0 ,小于 0 180 的条件,球面三角形都成立. 注: c 边和 C 角在写法上的区别. 例 判断下面的球面三角形是否存在. 1. 0 A =100 , 0 B =170 , 0 C = 70 . 解 ∵ 0 0 A B C + − = 200 180 ,∴球面三角形不存在. 2. 0 a =100 , 0 b =170 , 0 c = 70 . 解 ∵ 0 a c b + = = 170 ,∴球面三角形不存在. 3. 0 A =100 , 0 B =100 , 0 C =100 . 解 ∵ 满足已知三角的三个条件,∴球面三角形存在. 图 4.2.7

4.a=100°,b=100°,c=100 解:满足已知三边的三个条件,“球面三角形存在 5.a=170°,b=170°,C=170°. 解:两个边及其夹角,都满足大于0°,小于180的条件,“球面三角形存在 练习题4.2 1.是非题 (1)球面直边三角形是指只有一个边为90°的球面三角形: (②)在同球上,边角对应相等的球面三角形称为球面全等三角形: (3)球面三角形三边之和大于0°,小于540°: (④球面三角形两角之和必小于第三角: (⑤)球面三角形外角小于相邻的两内角之和. 2.由极线上任一点和极线相连的大圆弧与极线构成怎样的球面角? 3.已知一球面三角形三个角分别为90°、90°、60°,试问该球面三角形的三边各为何值? 4.判断新下列球面三角形是否存在: (1)a=110°,b=60°,c=50°:(2)A=110°,B=60°,C=50°: (3)a=120°,b=120,c=120:(4)A=120°,B=120°,C=120° (5)a=100°,b=170°,c=90°:(6)A=100°,B=170°,C=90°: (7)a=60°,b=60°,c=60°:(8)A=60°,B=60°,C=60°: (9)a=1°,B=179°,c=179°:(10)A=28°,b=179°,C=181° 5.设球面三角形ABC的三边为a、b、c,且a>b>c,它的极线三角形的三边为d、b、 c,求证:d<b<c. 6.在球面三角形ABC中,设A=90°,且B>C,求证: (1)2700>B+C>90°:(2)B-C<90°. 7.在球面三角形ABC中,设a=90°,求证:
84 4. 0 a =100 , 0 b =100 , 100o c = . 解 ∵ 满足已知三边的三个条件,∴球面三角形存在. 5. 0 a =170 , 0 b =170 , 0 C =170 . 解 ∵两个边及其夹角,都满足大于 0 0 ,小于 0 180 的条件,∴球面三角形存在. 练习题 4.2 1. 是非题 (1)球面直边三角形是指只有一个边为 0 90 的球面三角形; (2)在同球上,边角对应相等的球面三角形称为球面全等三角形; (3)球面三角形三边之和大于 0 0 ,小于 0 540 ; (4)球面三角形两角之和必小于第三角; (5)球面三角形外角小于相邻的两内角之和. 2.由极线上任一点和极线相连的大圆弧与极线构成怎样的球面角? 3.已知一球面三角形三个角分别为 0 90 、 0 90 、 0 60 ,试问该球面三角形的三边各为何值? 4.判断下列球面三角形是否存在: (1) 0 a =110 , 0 b = 60 , 0 c = 50 ; (2) 0 A =110 , 0 B = 60 , 0 C = 50 ; (3) 0 a =120 , 0 b =120 , 0 c =120 ; (4) 0 A =120 , 0 B =120 , 0 C =120 ; (5) 0 a =100 , 0 b =170 , 0 c = 90 ; (6) 0 A =100 , 0 B =170 , 0 C = 90 ; (7) 0 a = 60 , 0 b = 60 , 0 c = 60 ; (8) 0 A = 60 , 0 B = 60 , 0 C = 60 ; (9) 0 a =1 , 0 B =179 , 0 c =179 ; (10) 0 A = 28 , 0 b =179 , 0 C =181 . 5.设球面三角形 ABC 的三边为 a、b 、c ,且 abc ,它的极线三角形的三边为 a 、b 、 c ,求证: abc . 6.在球面三角形 ABC 中,设 0 A = 90 ,且 B C ,求证: (1) 0 0 270 90 + B C ;(2) 0 B C− 90 . 7. 在球面三角形 ABC 中,设 0 a = 90 ,求证:

(1)270°>b+c>90°:(2)b-c<90° 8.在球面三角形ABC中,求证: D-90°<(4+B-C)<90:(2)0°<a+b-c<180 9.如图4.2.8,AP、BP、CP、DP、EP和ABCDE都是大圆弧,求证 ∠APB+∠BPC+∠CPD+∠DPE+∠EPA=36O° 图4.2.8 图4.2.9 10.如图4.2.9,球面上P点是大圆弧QER的极,Z点是大圆弧SEN的极,求证 (1)SE=EN=QE=ER=90°:(2)ZP=SQ,OZ=PN. 4.3球面三角形公式 4.3.1余弦公式 1、边的余弦公式: 球面三角形一个边的余弦等于其它两边余弦的乘积加上这两边正弦及其夹角余弦的乘 cosa=cosbcosc+sin bsin ccos d cosb=cos a cosc+sin asin ccos B (4.3.1) cosc=cosacosb+sin asin bcosC 公式(4.3.1)通常用于求解已知两边及其夹角求第三边或者已知三边求一角。它在航海 实际工作中是最常用的公式之一,如求起航点与到达点之间的距离。 2、角的余弦公式 球面三角形一个角的余弦等于其它两角余弦的乘积冠以负号加上这两角正弦及其夹边 女
85 (1) 0 0 270 90 + b c ;(2) 0 b c − 90 . 8.在球面三角形 ABC 中,求证: (1) ( ) 0 0 1 90 90 2 − + − A B C ;(2) ( ) 0 0 1 0 180 2 + − a b c . 9. 如图 4.2.8, AP 、 BP 、CP 、 DP、 EP 和 ABCDE 都是大圆弧,求证: 0 + + + + = APB BPC CPD DPE EPA 360 . 图 4.2.8 图 4.2.9 10.如图 4.2.9,球面上 P 点是大圆弧 QER 的极, Z 点是大圆弧 SEN 的极,求证: (1) 0 SE EN QE ER = = = = 90 ;(2) ZP SQ = ,QZ PN = . 4.3 球面三角形公式 4.3.1 余弦公式 1、边的余弦公式: 球面三角形一个边的余弦等于其它两边余弦的乘积加上这两边正弦及其夹角余弦的乘 积. = + = + = + c a b a b C b a c a c B a b c b c A cos cos cos sin sin cos cos cos cos sin sin cos cos cos cos sin sin cos (4.3.1) 公式(4.3.1)通常用于求解已知两边及其夹角求第三边或者已知三边求一角. 它在航海 实际工作中是最常用的公式之一,如求起航点与到达点之间的距离. 2、角的余弦公式: 球面三角形一个角的余弦等于其它两角余弦的乘积冠以负号加上这两角正弦及其夹边