
§1.3向量组的线性表出关系 1.定义3: ().组男可由组4线性表出:记作男→: (2).组男与组4等价(即可互相线性表出):记作男@4 2.例: (1).子组→大组: (例如:{a1,a2}→{a1,a2,a3}) (2).(矩阵)AB的行组→B的行组: (宏观地看AB的行) 3.传递性 日.6一》.穷一→三名一→6 2),6一项,男字y三6 张南同济大学 6131
§1.3 向量组的线性表出关系 1. 定义 3: (1). 组 B 可由组 A 线性表出: 记作 B → A ; (2). 组 B 与组 A 等价 (即可互相线性表出): 记作 B ↔ A . 2. 例 : (1). 子组 → 大组; (例如:{a1, a2} → {a1, a2, a3}) (2). (矩阵)AB 的行组 → B 的行组; (宏观地看 AB 的行.) 3. 传递性: (1). C → B, B → A ⇒ C → A . (2). C ↔ B, B ↔ A ⇒ C ↔ A . ᕖ㦿 (ੂ⎄大ᆜ) 线性代数 6 / 31

§1.3向量组的线性表出关系 1.定义3: ().组男可由组线性表出:记作男→: (2).组男与组4等价(即可互相线性表出):记作男台 2.例: (1).子组→大组: (例如:{a1,a2}→{a1,a2,a3}) (2).(矩阵)AB的行组→B的行组: (宏观地看AB的行) 3.传递性: (1).6→男,男十→6→d. 2.6→8.字y一6 张南同济大学 6/31
§1.3 向量组的线性表出关系 1. 定义 3: (1). 组 B 可由组 A 线性表出: 记作 B → A ; (2). 组 B 与组 A 等价 (即可互相线性表出): 记作 B ↔ A . 2. 例 : (1). 子组 → 大组; (例如:{a1, a2} → {a1, a2, a3}) (2). (矩阵)AB 的行组 → B 的行组; (宏观地看 AB 的行.) 3. 传递性: (1). C → B, B → A ⇒ C → A . (2). C ↔ B, B ↔ A ⇒ C ↔ A . ᕖ㦿 (ੂ⎄大ᆜ) 线性代数 6 / 31

§1.3向量组的线性表出关系 1.定义3: ().组男可由组线性表出:记作男→: (2).组男与组4等价(即可互相线性表出):记作男台 2.例: (1).子组→大组: (例如:{a1,a2}→{a1,a2,a3}) (2).(矩阵)AB的行组→B的行组: (宏观地看AB的行) 3.传递性: (1).省→男,男→→6→. (2).6日男,男台→6. 张南同济大学 6/31
§1.3 向量组的线性表出关系 1. 定义 3: (1). 组 B 可由组 A 线性表出: 记作 B → A ; (2). 组 B 与组 A 等价 (即可互相线性表出): 记作 B ↔ A . 2. 例 : (1). 子组 → 大组; (例如:{a1, a2} → {a1, a2, a3}) (2). (矩阵)AB 的行组 → B 的行组; (宏观地看 AB 的行.) 3. 传递性: (1). C → B, B → A ⇒ C → A . (2). C ↔ B, B ↔ A ⇒ C ↔ A . ᕖ㦿 (ੂ⎄大ᆜ) 线性代数 6 / 31
定理: 设(列向量组对={a1,·,am}和男={b1,…,b, 记矩阵:A=(a1,·,am)和B=(b1,·,b), 则:男→÷矩阵方程AX=B有解台R(A)=R(A,B) 4.证功一司一硬个b,一0=1,,m 一每个线性方程组x=b,部有解,0=1,一, 一矩阵方程:,0=(b1…,)有解 =矩阵方程三B有解 =R4)=R(4.B 张同济大学 维物 7/31
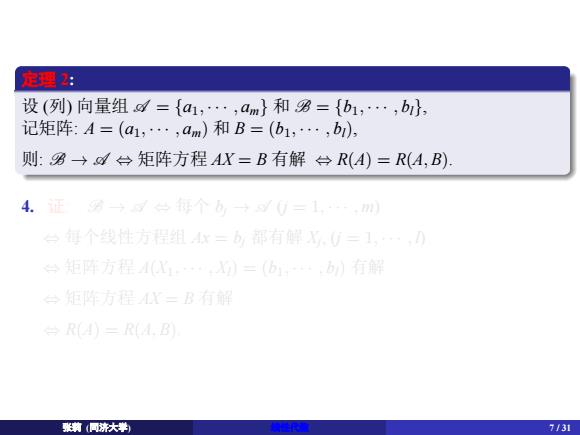
. 定理 2: . . 设 (列) 向量组 A = {a1, · · · , am} 和 B = {b1, · · · , bl}, 记矩阵: A = (a1, · · · , am) 和 B = (b1, · · · , bl), 则: B → A ⇔ 矩阵方程 AX = B 有解 ⇔ R(A) = R(A, B). 4. 䇷: B → A ⇔ 每个 bj → A (j = 1, · · · , m) ⇔ 每个线性方程组 Ax = bj 都有解 Xj , (j = 1, · · · , l) ⇔ 矩阵方程 A(X1, · · · , Xl) = (b1, · · · , bl) 有解 ⇔ 矩阵方程 AX = B 有解 ⇔ R(A) = R(A, B). ᕖ㦿 (ੂ⎄大ᆜ) 线性代数 7 / 31

定理2: 设(列)向量组={a,…,am}和男={b1,·,b} 记矩阵:A=(a1,·,am)和B=(b1,…,b), 则:男→÷矩阵方程AX=B有解÷R(A)=R(A,B) 4.证:男→4台每个b→a40=1,·,m) 台每个线性方程组x=b都有解X,0=1,…·,) 台矩阵方程A(X1,·,X)=(b1,·,b)有解 ÷矩阵方程AX=B有解 台R(A)=R(A,B): 张鞘同济大学 维代物 7/31
. 定理 2: . . 设 (列) 向量组 A = {a1, · · · , am} 和 B = {b1, · · · , bl}, 记矩阵: A = (a1, · · · , am) 和 B = (b1, · · · , bl), 则: B → A ⇔ 矩阵方程 AX = B 有解 ⇔ R(A) = R(A, B). 4. 䇷: B → A ⇔ 每个 bj → A (j = 1, · · · , m) ⇔ 每个线性方程组 Ax = bj 都有解 Xj , (j = 1, · · · , l) ⇔ 矩阵方程 A(X1, · · · , Xl) = (b1, · · · , bl) 有解 ⇔ 矩阵方程 AX = B 有解 ⇔ R(A) = R(A, B). ᕖ㦿 (ੂ⎄大ᆜ) 线性代数 7 / 31