试验设计与分析 试验设计方法 (4)n,p,q取值对应表 由(式3)我们可以算出n取不同值的p、q的取值。 n、 q、p取值对应表 n p q n p q 2 0.966 0.2590 9 0.8780.171 3 0.9430 0.2360 10 0.8720 0.165 4 0.9260 0.2190 11 0.86500.1580 5 0.911 0.2040 12 0.8610 0.1540 6 0.9010 0.1940 13 0.85500.1480 7 0.8920 0.185 14 0.8540 0.147 8 0.8830 0.1760 15 0.8480 0.141
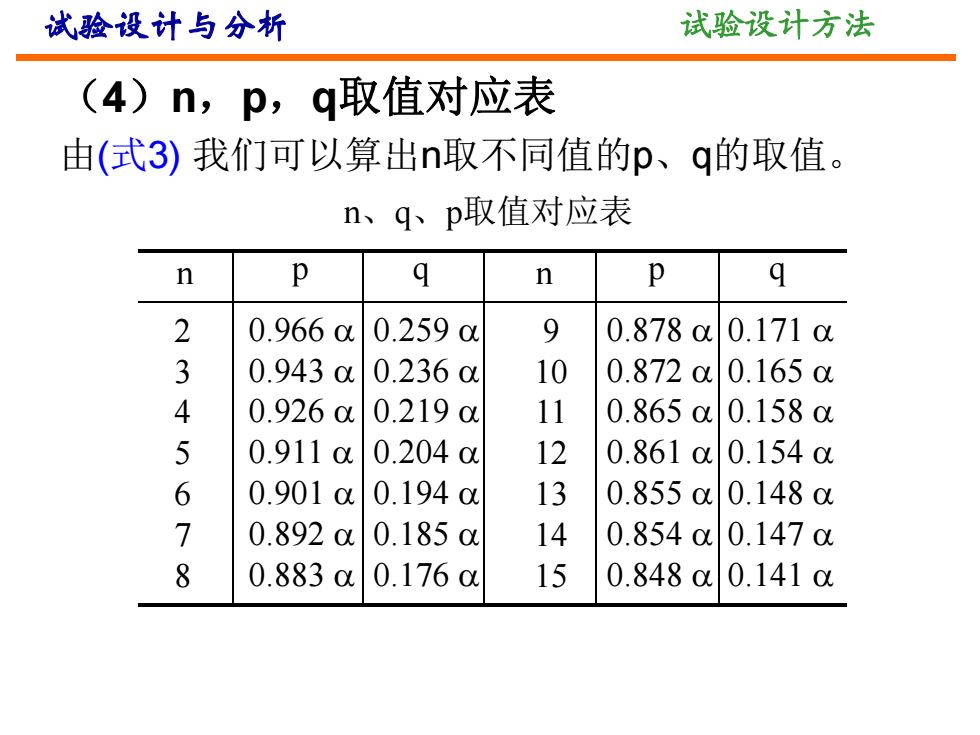
试验设计与分析 试验设计方法 (4)n,p,q取值对应表 由(式3) 我们可以算出n取不同值的p、q的取值。 n 2 3 4 5 6 7 8 p q n 9 10 11 12 13 14 15 p q 0.966 0.943 0.926 0.911 0.901 0.892 0.883 0.259 0.236 0.219 0.204 0.194 0.185 0.176 0.878 0.872 0.865 0.861 0.855 0.854 0.848 0.171 0.165 0.158 0.154 0.148 0.147 0.141 n、q、p取值对应表

试验设计与分析 试验设计方法 (5)小结 对两因素问题A、B、C构成初始单纯形,在此三点进行试验 规则1:去掉最坏点,用其对称反射点作新试点 例A、B、C中,若A为最坏点,去掉A点并取A的对称点D点 作为新试验点。 D=[留下各点之和]一[去掉点]=B十C一A 在B、C、D三角形中继续使用规则1,如果C为坏点,去点C 点,取其反点E,此时C、D、E三点又构成新的单纯形。 如果最坏点为D那么对称点就会返回到与A重合,此时改用规 则2
试验设计与分析 试验设计方法 (5)小结 对两因素问题A、B、C构成初始单纯形,在此三点进行试验 规则1:去掉最坏点,用其对称反射点作新试点 例A、B、C中,若A为最坏点,去掉A点并取A的对称点D点 作为新试验点。 D=[留下各点之和]-[去掉点]=B+C-A 在B、C、D三角形中继续使用规则1,如果C为坏点,去点C 点,取其反点E,此时C、D、E三点又构成新的单纯形。 如果最坏点为D那么对称点就会返回到与A重合,此时改用规 则2

试验设计与分析 试验设计方法 规则2:去掉次坏点,用其对称反射点作新试点对称计算公 式与前面相同。 经过反复使用后,如果有一个点老是保留下来,必须使用规 则3 规则3:重复、停止和缩短步长 一般一个点经3次单纯形后仍未被淘汰,它可能是一个很好 点,也可能是偶然性或试验误差导致的假象。 此时需要重复试验:结果不好,淘汰;结果已很满意则停止 试验,反之则以它为起点缩短步长,继续试验
试验设计与分析 试验设计方法 规则2:去掉次坏点,用其对称反射点作新试点对称计算公 式与前面相同。 经过反复使用后,如果有一个点老是保留下来,必须使用规 则3 规则3:重复、停止和缩短步长 一般一个点经3次单纯形后仍未被淘汰,它可能是一个很好 点,也可能是偶然性或试验误差导致的假象。 此时需要重复试验:结果不好,淘汰;结果已很满意则停止 试验,反之则以它为起点缩短步长,继续试验

试验设计与分析 试验设计方法 (6)特殊方法 前面介绍的单纯形是正规的,任意两点间的距离一样,实际 上,这个要求可以不要。尤其是由于各个因素所取的量纲不 一样(例如一个因素是温度(℃),另一个因素是时间(秒 )。即使量纲一样所取的单位也可以不一样。 (一)直角单纯形法 我们考虑双因素模型,开始不从正三角形出发,而是从一个 直角三角形出发,其顶点取值如下: @=(a1,a2) ①=(a1+p1,a2) ②=(a1,a2+p2) 用图表示如下
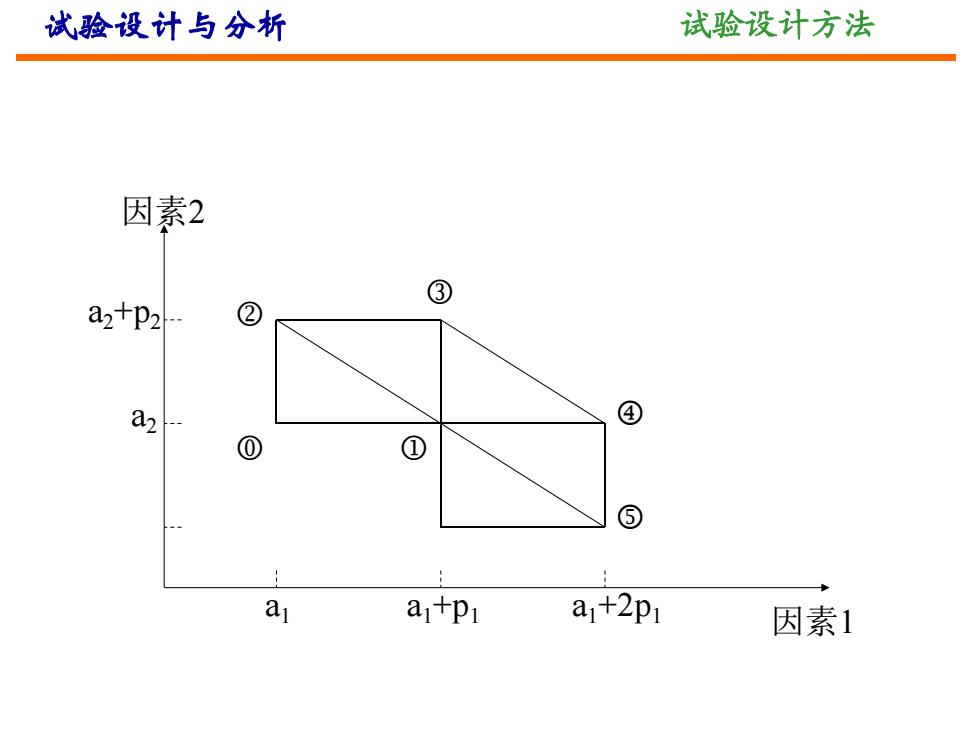
试验设计与分析 试验设计方法 (6)特殊方法 前面介绍的单纯形是正规的,任意两点间的距离一样,实际 上,这个要求可以不要。尤其是由于各个因素所取的量纲不 一样(例如一个因素是温度(℃),另一个因素是时间(秒 )。即使量纲一样所取的单位也可以不一样。 (一)直角单纯形法 我们考虑双因素模型,开始不从正三角形出发,而是从一个 直角三角形出发,其顶点取值如下: =(a1,a2) =(a1+p1,a2) =(a1,a2+p2) 用图表示如下
试验设计与分析 试验设计方法 因素2 ③ a2+p2 ② a2 ④ O ① ⑤ al a1+p1 a1+2p1 因素1
试验设计与分析 试验设计方法 a2+p2 a2 a1 a1+p1 a1+2p1 因素2 因素1