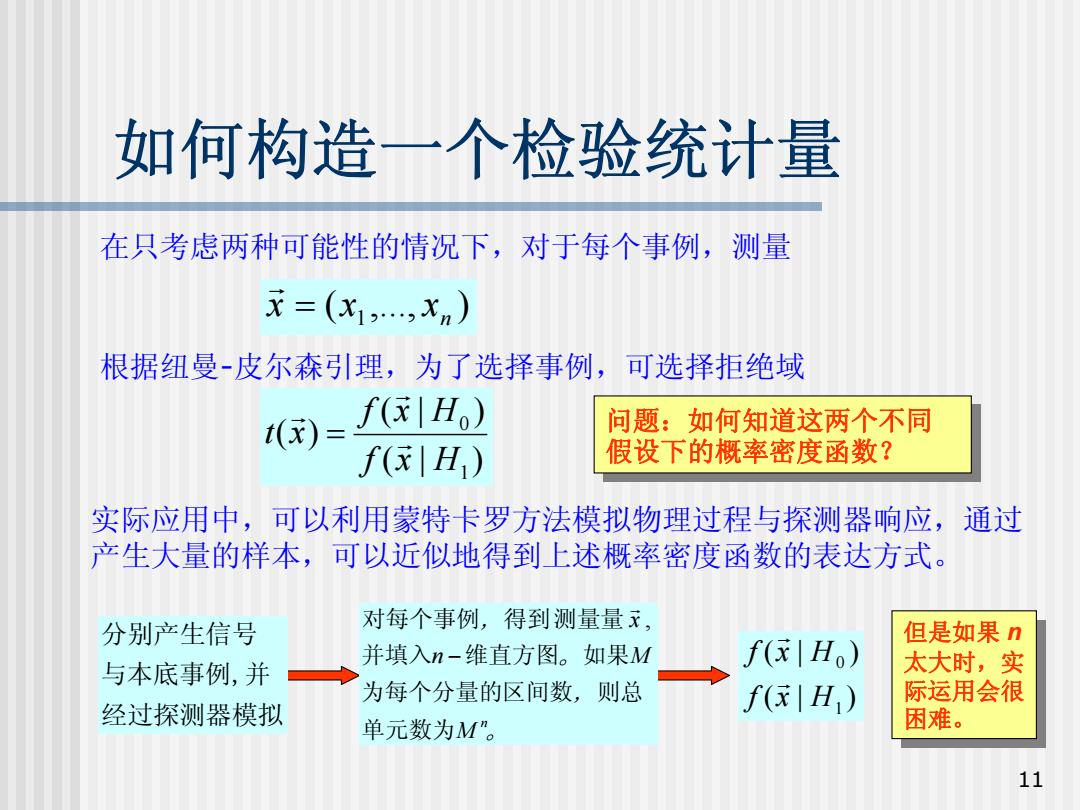
如何构造一个检验统计量 在只考虑两种可能性的情况下,对于每个事例,测量 元=(x1,,Xn) 根据纽曼-皮尔森引理,为了选择事例,可选择拒绝域 ()= f(H) 问题:如何知道这两个不同 f(|H) 假设下的概率密度函数? 实际应用中,可以利用蒙特卡罗方法模拟物理过程与探测器响应,通过 产生大量的样本,可以近似地得到上述概率密度函数的表达方式。 分别产生信号 对每个事例,得到测量量元, 但是如果n 并填入n-维直方图。如果M f(|H) 与本底事例,并 太大时,实 为每个分量的区间数,则总 际运用会很 经过探测器模拟 f(|H) 单元数为M”。 困难。 11
11 如何构造一个检验统计量 根据纽曼 -皮尔森引理,为了选择事例,可选择拒绝域 ( ,..., ) 1 n x = x x G ( | ) ( | ) ( ) 1 0 f x H f x H t x G G G = 问题:如何知道这两个不同 假设下的概率密度函数? 问题:如何知道这两个不同 假设下的概率密度函数? 实际应用中,可以利用蒙特卡罗方法模拟物理过程与探测器响应,通过 产生大量的样本,可以近似地得到上述概率密度函数的表达方式。 ( | ) ( | ) 1 0 f x H f x H G G 在只考虑两种可能性的情况下,对于每个事例,测量 M 。 , n 。 M , x 单元数为 n 为每个分量的区间数 则总 并填入 维直方图 如果 对每个事例 得到测量量 − , G 分别产生信号 与本底事例,并 经过探测器模拟 但是如果 n 太大时,实 际运用会很 困难。 但是如果 n 太大时,实 际运用会很 困难
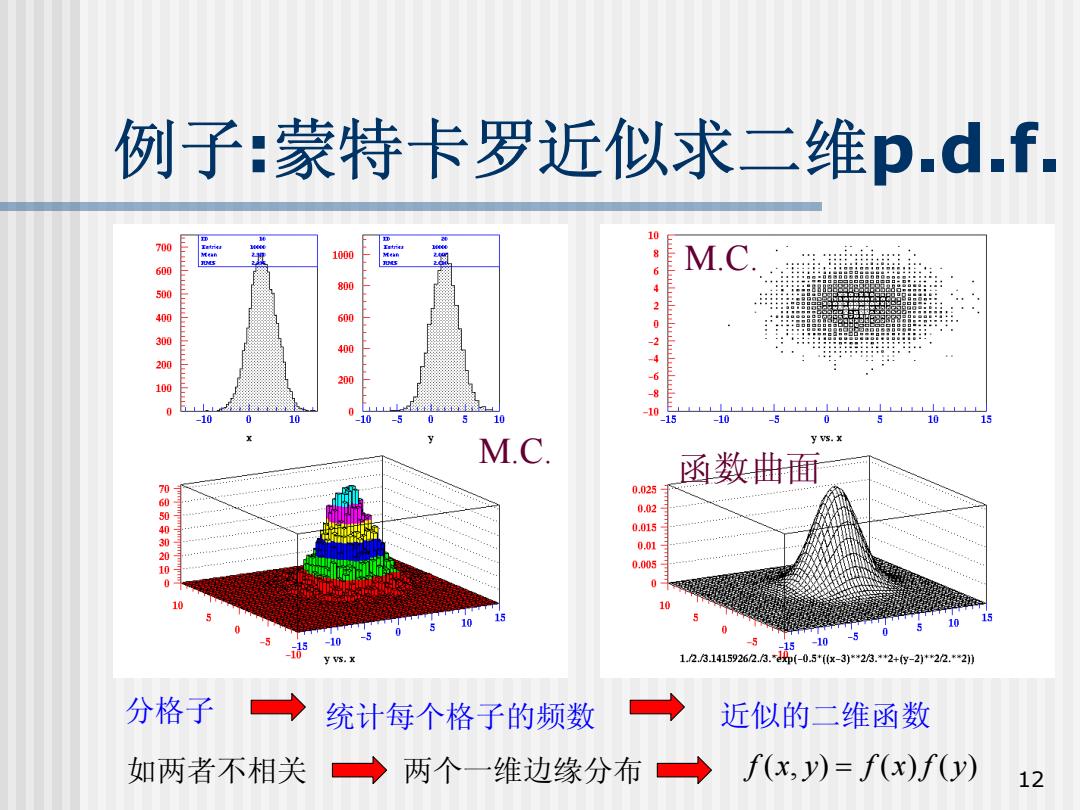
例子:蒙特卡罗近似求二维p.d.f. 10 700 1000 600 86 M 800 4 2 600 100 200 0246810 M.C. 函数曲面 0.025 0.02 0.015 0.01 0.005 0 10 10 10 15 -10 1.2.3.14159262.3.*0(-0.5*x-3*23.*2+y-21*22.*2) 分格子 → 统计每个格子的频数 近似的二维函数 如两者不相关 →两个一维边缘分布 f(x,y)=f(x)f(y) 12
12 例子:蒙特卡罗近似求二维p.d.f. M.C. M.C. 函数曲面 分格子 统计每个格子的频数 近似的二维函数 如两者不相关 两个一维边缘分布 f ( , x y f ) = (x) f y( )