
二、总体回归函数 Population Regression Function, PRF
二、总体回归函数 Population Regression Function, PRF

1、条件均值(conditional mean) 例2.1:一个假想的社区有100户家庭组成, 欲研究该社区每月家庭消费支出Y与每月 家庭可支配收入X的关系。即如果知道了 家庭的月收入,能否预测该社区家庭的平 均月消费支出水平。 ·为达到此目的,将该100户家庭划分为组 内收入差不多的10组,以分析每一收入组 的家庭消费支出
1、条件均值(conditional mean) • 例2.1:一个假想的社区有100户家庭组成, 欲研究该社区每月家庭消费支出Y与每月 家庭可支配收入X的关系。 即如果知道了 家庭的月收入,能否预测该社区家庭的平 均月消费支出水平。 • 为达到此目的,将该100户家庭划分为组 内收入差不多的10组,以分析每一收入组 的家庭消费支出
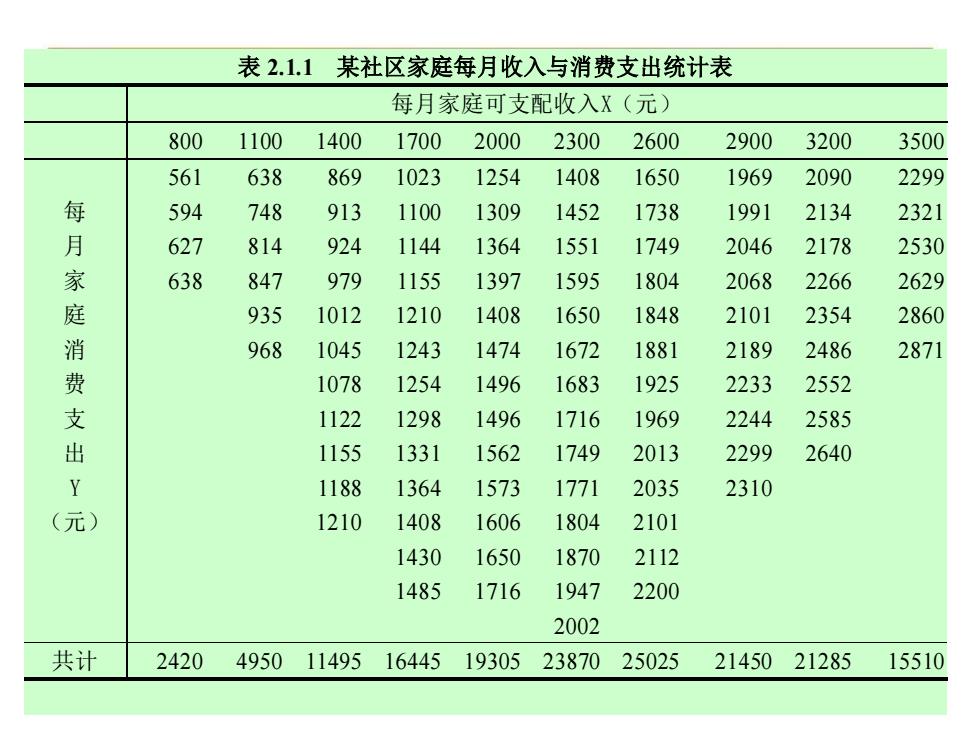
表2.1.1 某社区家庭每月收入与消费支出统计表 每月家庭可支配收入X(元) 800 1100 1400 1700 2000 2300 2600 2900 3200 3500 561 638 869 1023 1254 1408 1650 1969 2090 2299 每 594 748 913 1100 1309 1452 1738 1991 2134 2321 月 627 814 924 1144 1364 1551 1749 2046 2178 2530 家 638 847 979 1155 1397 1595 1804 2068 2266 2629 庭 935 1012 1210 1408 1650 1848 2101 2354 2860 消 968 1045 1243 1474 1672 1881 2189 2486 2871 费 1078 1254 1496 1683 1925 2233 2552 支 1122 1298 1496 1716 1969 2244 2585 出 1155 1331 1562 1749 2013 2299 2640 Y 1188 1364 1573 1771 2035 2310 (元) 1210 1408 1606 1804 2101 1430 1650 1870 2112 1485 1716 1947 2200 2002 共计 2420 4950 11495 16445 19305 23870 25025 2145021285 15510
表 2.1.1 某社区家庭每月收入与消费支出统计表 每月家庭可支配收入X(元) 800 1100 1400 1700 2000 2300 2600 2900 3200 3500 561 638 869 1023 1254 1408 1650 1969 2090 2299 594 748 913 1100 1309 1452 1738 1991 2134 2321 627 814 924 1144 1364 1551 1749 2046 2178 2530 638 847 979 1155 1397 1595 1804 2068 2266 2629 935 1012 1210 1408 1650 1848 2101 2354 2 86 0 968 1045 1243 1474 1672 1881 2189 2486 2871 1078 1254 1496 1683 1925 2233 2552 1122 1298 1496 1716 1969 2244 2585 1155 1331 1562 1749 2013 2299 2640 1188 1364 1573 1771 2035 2310 1210 1408 1606 1804 2101 1430 1650 1870 2112 1485 1716 1947 2200 每 月 家 庭 消 费 支 出 Y (元) 2002 共 计 2420 4950 11495 16445 19305 23870 25025 21450 21285 15510

● 由于不确定因素的影响,对同一收入水平X,不同家 庭的消费支出不完全相同; 但由于调查的完备性,给定收入水平X的消费支出Y的 分布是确定的,即以X的给定值为条件的Y的条件分布 (Conditional distribution)是已知的,例如: P(Y=561X=800)=1/4。 因此,给定收入X的值X1,可得消费支出Y的条件均值 (conditional mean)或条件期望(conditional expectation):E(Y X=Xi). 该例中:E(YX=800)=605
• 由于不确定因素的影响,对同一收入水平X,不同家 庭的消费支出不完全相同; • 但由于调查的完备性,给定收入水平X的消费支出Y的 分布是确定的,即以X的给定值为条件的Y的条件分布 (Conditional distribution)是已知的,例如: P(Y=561|X=800)=1/4。 • 因此,给定收入X的值Xi,可得消费支出Y的条件均值 (conditional mean)或条件期望(conditional expectation):E(Y|X=Xi)。 • 该例中:E(Y | X=800)=605
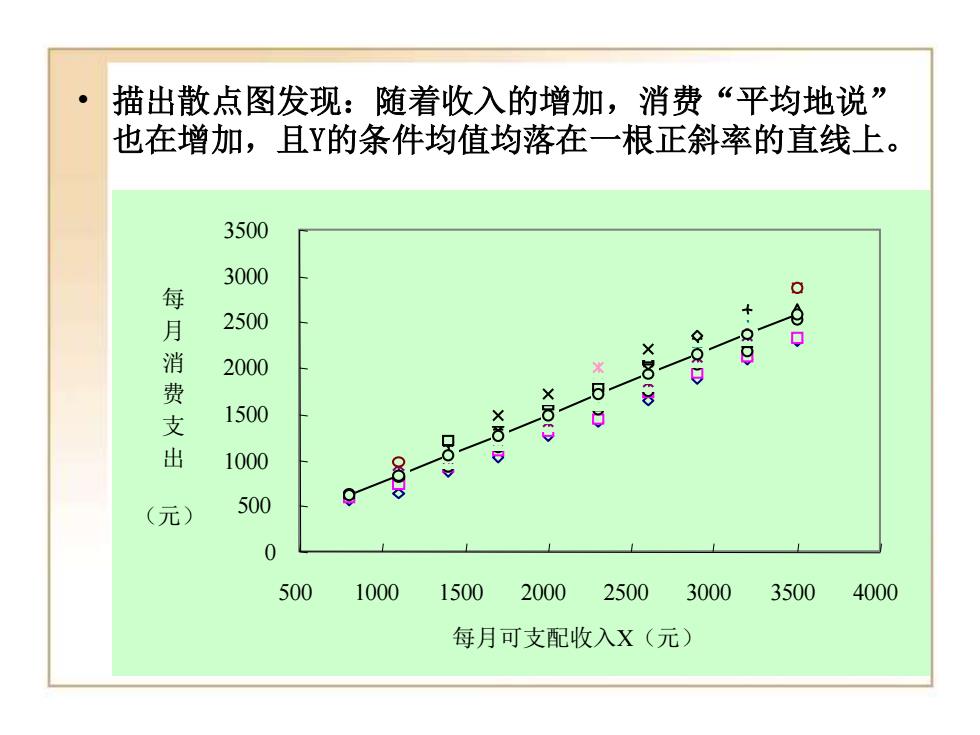
描出散点图发现:随着收入的增加,消费“平均地说” 也在增加,且Y的条件均值均落在一根正斜率的直线上。 3500 3000 每 月 2500 消 2000 费 -6 支 1500 出 1000 (元) 500 0 500 1000 150020002500 3000 3500 4000 每月可支配收入X(元)
• 描出散点图发现:随着收入的增加,消费“平均地说” 也在增加,且Y的条件均值均落在一根正斜率的直线上。 0 500 1000 1500 2000 2500 3000 3500 500 1000 1500 2000 2500 3000 3500 4000 每月可支配收入X(元) 每 月 消 费 支 出 Y (元)