
④ 将x→X换成x→x,x→x0,X→+0,x→-0, X→0 仍有类似的结论 如:x→0时型的极限 定理 设f(x),g(x)在|x>N上有定义,且 (1)lim f(x)=lim g(x)=0 K-oo K-0o (2)f(x)g(x)在|x>N时可导,且g'(x)≠0 I(x (3)lim g(x) =A或o0) 则im f(x)=lim f'(x) =A(或oo) x-→°g(x) xo g'(x)
④ → → → → → + → − + − x x x x x , x x , x , x , 将 0换成 0 0 仍有类似的结论 时 型的极限 0 0 如: x → 定理 ( ) ( ) ( ) lim ( ) ( ) lim ( ) ( ) ( ) (3)lim (2) ( ), ( ) | | ( ) 0 (1)lim ( ) lim ( ) 0 ( ), ( ) | | = = = = = → → → → → 则 或 或 在 时可导,且 设 在 上有定义,且 A g x f x g x f x A g x f x f x g x x N g x f x g x f x g x x N x x x x x

关于°型的极限,有下述定理 定理 设f(x),g(x)在x的某邻域内有定义,且 (1)lim f(x)=lim g(x)=o x→x0 x→x0 (2)f(x),g(x)可导,且g'(x)≠0 (3)lim'(x =A或o) x→xog'(x) 则im f(x)=lim f'(x) x-→wg(x)x→xg'(x) =A(或oo) 将x→X换成x→x,x→x,x→十0,x→-∞, X→0 结论仍成立
关于 型的极限,有下述定理 定理 ( ) ( ) ( ) lim ( ) ( ) lim ( ) ( ) ( ) (3) lim (2) ( ), ( ) ( ) 0 (1) lim ( ) lim ( ) ( ), ( ) 0 0 0 0 0 0 = = = = = → → → → → 则 或 或 可导,且 设 在 的某邻域内有定义,且 A g x f x g x f x A g x f x f x g x g x f x g x f x g x x x x x x x x x x x x → → → → → + → − + − x x x x x , x x , x , x , 将 0换成 0 0 结论仍成立
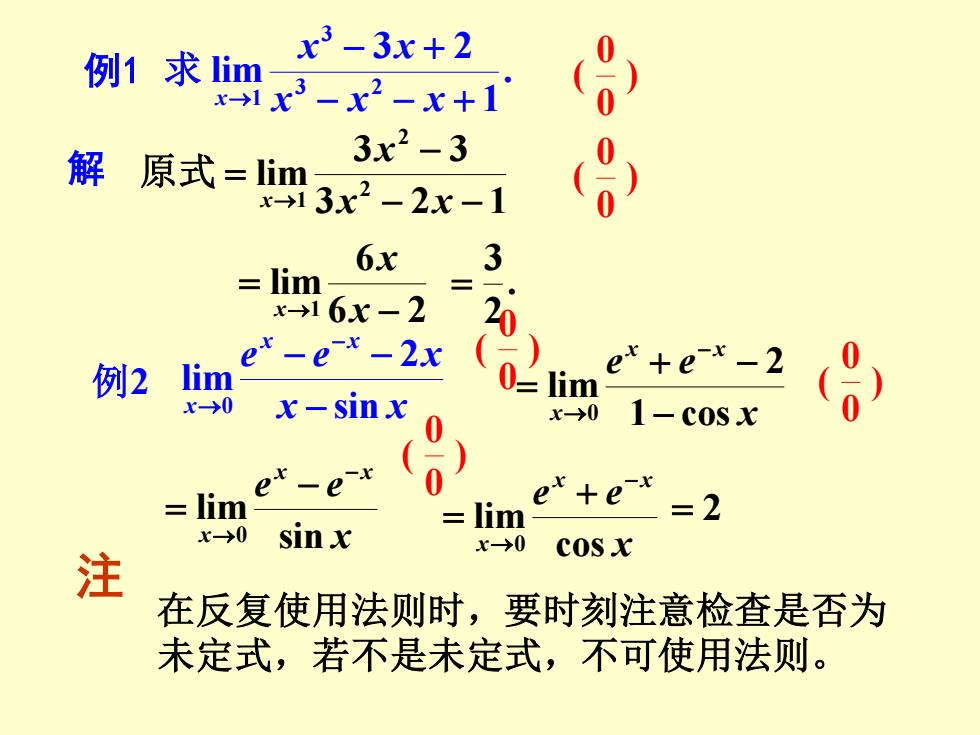
x3-3x+2 例1求im →1x3-x2-x+1 0) 解 原式=im 3x2-3 x13x2-2x-1 6x 3 lim x→16x-2 ex-e x-2x 例2 lim '+e-x-2 x-→0 x-sinx 0-1im x-→0 0 1-cosx ex-e-x lim lim =2 x-→0 sinx X→0 COSX 注 在反复使用法则时,要时刻注意检查是否为 未定式,若不是未定式,不可使用法则
例1 . 1 3 2 lim 3 2 3 1 − − + − + → x x x x x x 求 ) 0 0 ( 解 3 2 1 3 3 lim 2 2 1 − − − = → x x x x 原式 ) 0 0 ( 6 2 6 lim 1 − = → x x x . 2 3 = 例2 x x e e x x x x sin 2 lim 0 − − − − → ) 0 0 ( x e e x x x 1 cos 2 lim 0 − + − = − → ) 0 0 ( x e e x x x sin lim 0 − → − = ) 0 0 ( x e e x x x cos lim 0 − → + = = 2 注 在反复使用法则时,要时刻注意检查是否为 未定式,若不是未定式,不可使用法则
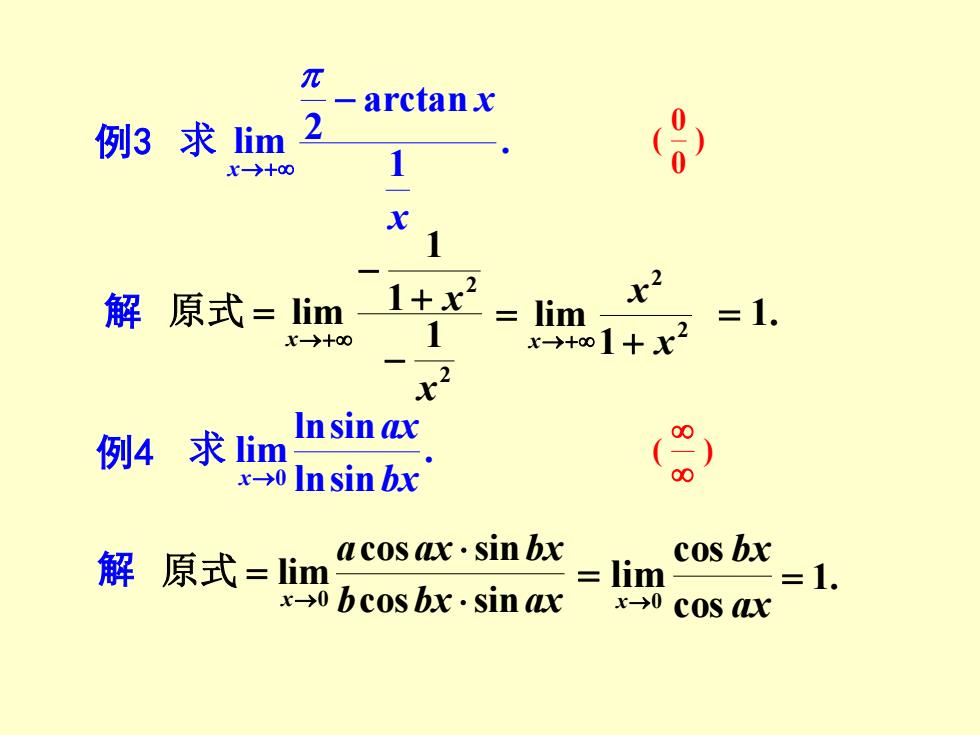
π -arctanx 例3求im2 X-→+00 .2 解原式=lim 1 lim 七2 X→+00 x+∞1+x2 比2 例4求im Insin ax x0 Insin bx 00 解原式=im .acos·sin bx cos bx =1. x-→0bc0sbx·sinx x-→0C0SX
例 3 解 . 1 arctan 2 lim x x x − →+ 求 2 2 1 1 1 lim x x x − + − = →+ 原式 2 2 1 lim x x x + = →+ = 1 . 例 4 解 . lnsin lnsin lim0 bx ax x → 求 b bx ax a ax bx x cos sin cos sin lim0 = → 原式 = 1 . ) 00 (( ) ax bx x cos cos lim→0 =