
代入边界条件:w(0)-0,w(U)=0D=0 C_gl24所以q(13 - 6lx2 + 4x3)0(x)24EIqx(13 - 21x2 + x3)w(x)24EIL5g14913mx =0,=-0:Wmx24EI384EI
代入边界条件:w(0)=0, w(l)=0 D=0 24 3 ql C = 所以 ( 2 ) 24 ( ) ( 6 4 ) 24 ( ) 3 2 3 3 2 3 l lx x EI qx w x l lx x EI q x = − + = − + EI ql w EI ql A B 384 5 , 24 4 max 3 max = = − = =

例5-3由积分法求图示梁的w、0。F解:1)坐标系如图:?Fa ElBLx2)分两段进行分析:xAC段:(0≤x≤a)yM(x)= -Fx则近似微分方程为:Elw"= -M(x)= Fx积分可得:EhW--Fx+C, Eh-IFP+Cx+D26BC段:(a≤x≤2a)M(x)--Fx+ Fa
M(x) = −Fx (0 x a) EIw = −M(x) = Fx 1 1 2 1 2 1 EIw = Fx +C 1 1 3 1 6 1 EIw = Fx +C x + D 例5-3 由积分法求图示梁的wA、A。 解:1) 坐标系如图; AC段: 则近似微分方程为: 积分可得: x y x x Fa a a F EI C A B 2) 分两段进行分析: BC段: (a x 2a) M(x) = −Fx+ Fa
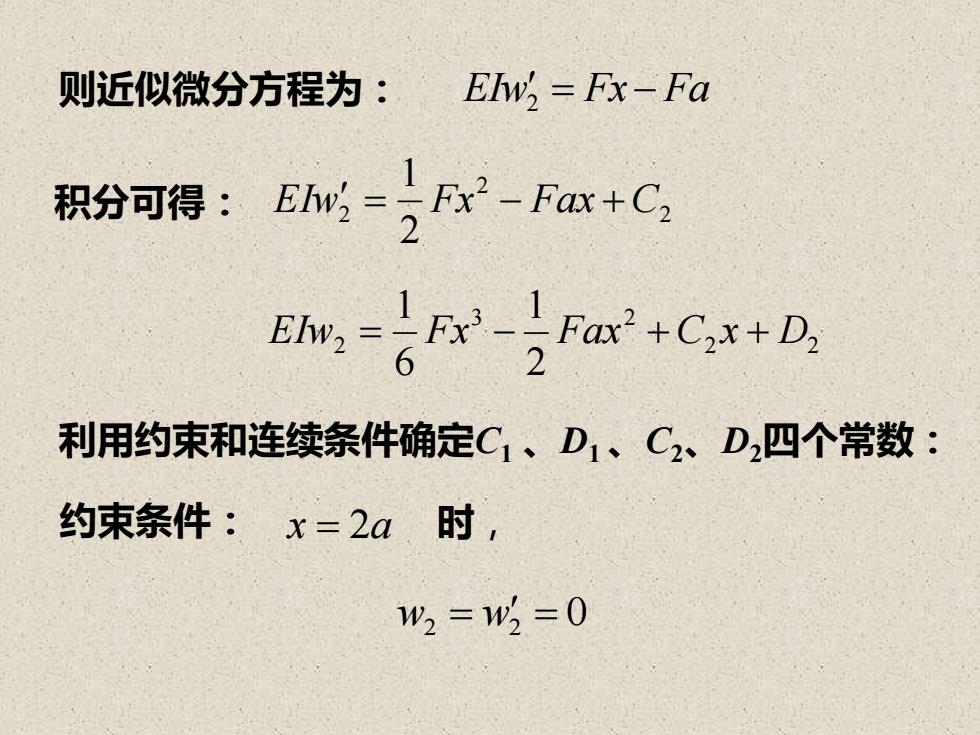
Elw, = Fx- Fa则近似微分方程为:积分可得: Ehwi=,Fx2-Fax+C,2Ew,-+Fx-}Fax+Cx+D,62利用约束和连续条件确定Ci、D,、C2、D,四个常数:约束条件:x=2a时,W2 = W = 0
EIw2 = Fx− Fa 2 2 2 2 1 EIw = Fx − Fax +C 2 2 3 2 2 2 1 6 1 EIw = Fx − Fax +C x + D 积分可得: 则近似微分方程为: 利用约束和连续条件确定C1 、D1 、C2、D2四个常数: 约束条件: x = 2a 时, w2 = w2 = 0

由此可得:C2 =02-Fa3D, =3连续条件:x=α 处, w,=w2;w=w2由此可得:Fa+Ca+D-Fa-Fa+=Fa3265Fa+C,-F-Fa22即:C--Fd,D-Fa6
连续条件: x = a 处, 2 2 1 2 2 1 2 1 Fa +C = Fa − Fa w1 w2 w1 w2 = ; = 由此可得: 3 3 3 1 1 3 3 2 2 1 6 1 6 1 Fa +C a + D = Fa − Fa + Fa 即: C1 = −Fa2 ; 3 1 6 7 D = Fa 由此可得: C2 = 0 3 2 3 2 D = Fa

最后可得:7Fa3WA = wilx-o = D, =(向下)6EI0,=W1.=C,=--Fd(逆时针)EI小结:(1)两段:四个常数,每增加一段,就增加两个积分常数;(2)由约束和连续条件求积分常数;(3)坐标原点一律放在左边,分段写出M(x);(4)注意x的范围
EI Fa w w D A x 6 7 3 = 1 0 = 1 = = EI Fa w C A x 2 1 0 1 = ' = = − = 最后可得: (向下) (逆时针) (2) 由约束和连续条件求积分常数; (1) 两段:四个常数,每增加一段,就增加 两个积分常数; 小结: (3) 坐标原点一律放在左边,分段写出M(x); (4) 注意x的范围