
材料力学第七章应力状态分析

第七章应力状态分析$ 7-1应力状态的概念$7-2平面应力状态分析—解析法$7-3平面应力状态分析一图解法$7-4梁的主应力及其主应力迹线$7-5三向应力状态研究一一应力圆法$77复杂应力状态下的应力一一应变关系(广义虎克定律)$7-8复杂应力状态下的变形比能A
第七章 应力状态分析 §7–1 应力状态的概念 §7–2 平面应力状态分析——解析法 §7–3 平面应力状态分析——图解法 §7–4 梁的主应力及其主应力迹线 §7–5 三向应力状态研究——应力圆法 §7–7 复杂应力状态下的应力 - 应变关系 ——(广义虎克定律) §7–8 复杂应力状态下的变形比能

应力状态与应变状态87-1应力状态的概念一、引言1、铸铁与低碳钢的拉、压、扭试验现象是怎样产生的?铸铁压缩铸铁拉伸CM低碳钢铸铁2、组合变形杆将怎样破坏?M
§7–1 应力状态的概念 一、引言 1、铸铁与低碳钢的拉、压、扭试验现象是怎样产生的? M 低碳钢 铸铁 P P 铸铁拉伸 P 铸铁压缩 2、组合变形杆将怎样破坏? M P
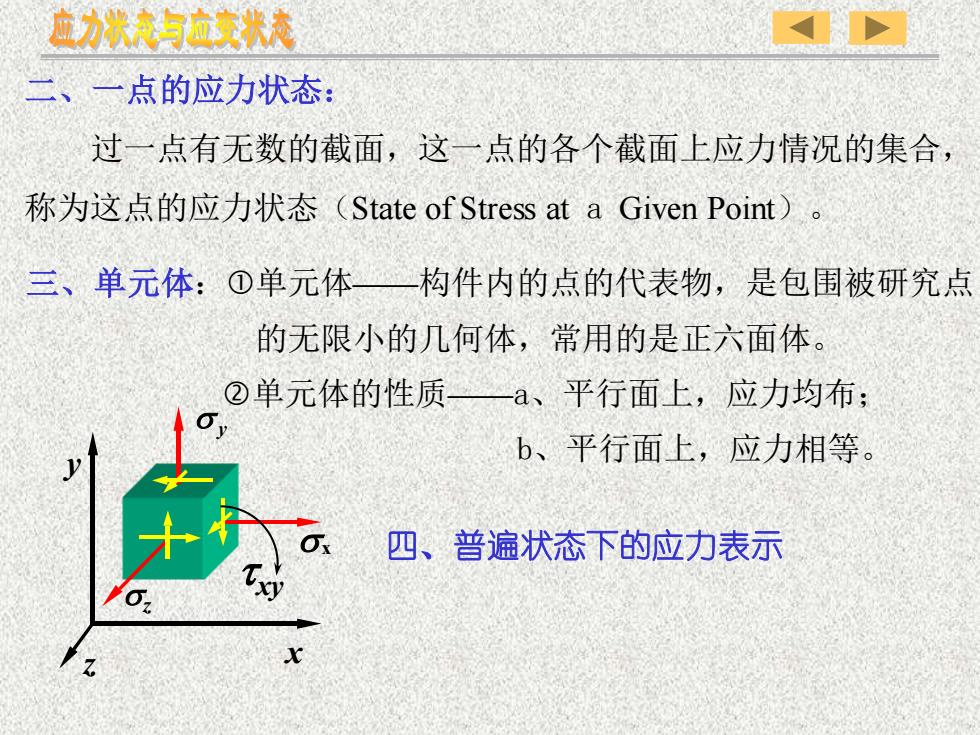
应力状夜与应变状表 二、一点的应力状态: 过一点有无数的截面,这一点的各个截面上应力情况的集合, 称为这点的应力状态(State of Stress at a Given Point)。 三、单元体:①单元体—构件内的点的代表物,是包围被研究点 的无限小的几何体,常用的是正六面体。 ②单元体的性质一—一a、平行面上,应力均布: b、平行面上,应力相等。 四、普遍状态下的应力表示
四、普遍状态下的应力表示 三、单元体:单元体——构件内的点的代表物,是包围被研究点 的无限小的几何体,常用的是正六面体。 单元体的性质——a、平行面上,应力均布; b、平行面上,应力相等。 二、一点的应力状态: 过一点有无数的截面,这一点的各个截面上应力情况的集合, 称为这点的应力状态(State of Stress at a Given Point)。 x y z sx sz s y txy

愈力状态与应卖状表 五、剪应力互等定理(Theorem of Conjugate Shearing Stress),: 过一点的两个正交面上,如果有与相交边垂直的剪应力分 量,则两个面上的这两个剪应力分量一定等值、方向相对或相 离。 证明单元体平衡∑M0 (dvdz)dx-(dzdx)dv=0 .Tx-T
x y z sx sz s y txy 五、剪应力互等定理(Theorem of Conjugate Shearing Stress): 过一点的两个正交面上,如果有与相交边垂直的剪应力分 量,则两个面上的这两个剪应力分量一定等值、方向相对或相 离。 证明: 单元体平衡 Mz =0 (t xydydz)dx−(t yxdzdx)dy=0 t xy =t yx