2、积分常数确定0位移边界条件:BWA =0, WB =08Wp =0, O,=0②连续条件:DWc左=Wo右③光滑条件:0c在=0c右
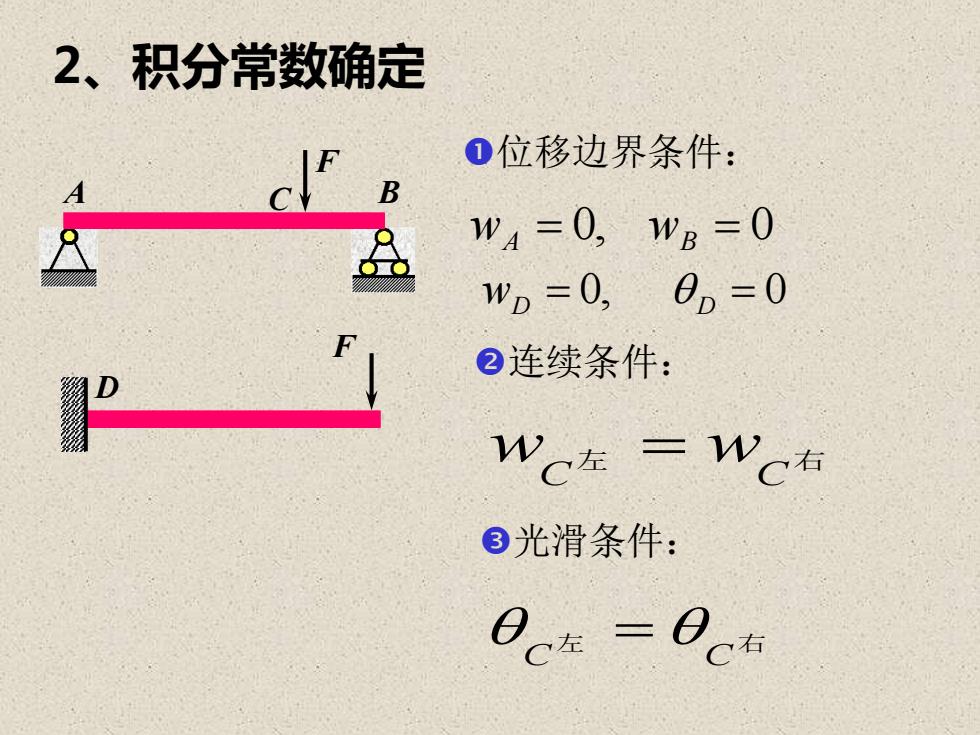
2、积分常数确定 F A C B F D wA = 0, wB = 0 wD = 0, D = 0 位移边界条件: 连续条件: 光滑条件: 左 右 C C = 左 右 wC wC =

例5-1由积分法求图示梁的wA、0。解:1、弯矩方程M(x)=-Fx2、微分方程及积分BAElw"=FxF2+CElw'=r2FElw=+Cx+ Dr.一6
例5-1 由积分法求图示梁的wA、A。 F A B l 解:1、弯矩方程 y x x M (x) = −Fx 2、微分方程及积分 x Cx D F EIw x C F EIw EIw Fx = + + = + = 3 2 6 2 '

3、确定积分常数FI?F13W=0,=D=x=l,w=0=C=234、转角方程,弯矩方程F2E(13-t)w=F(x3 - 31’x+21)W6EI5、最大转角和最大挠度FI?(逆时针)W.A=2EIF13(向下)WA3EI
3、确定积分常数 3 ; 0, 2 , ' 0 2 3 Fl w D Fl x = l w = C = − = = 4、转角方程,弯矩方程 ( 3 2 ) 6 ( ) 2 ' 3 2 3 2 2 x l x l EI F w l x EI F w = − + = − 5、最大转角和最大挠度 (向下) (逆时针) EI Fl w EI Fl w A A 3 2 ' 3 2 = = −

积分法求解梁位移的思路:①建立合适的坐标系;②求弯矩方程M(x):Elw"=-M(x)③建立近似微分方程:根据本书的规定坐标系,取负号进行分析。积分求Elw'和Elw;③用约束条件或连续条件,确定积分常数;③一般求极值可用数学方法,也可由挠曲线直接判别
EIw = −M(x) 积分法求解梁位移的思路: ① 建立合适的坐标系; ② 求弯矩方程M(x) ; ③ 建立近似微分方程: ⑤ 用约束条件或连续条件,确定积分常数; ⑥ 一般求极值可用数学方法,也可由挠曲线直接 判别。 根据本书的规定坐标系,取负号进行分析。 ④ 积分求 EIw 和 EIw;

例5-2图示简支梁受分布力作用,确定其挠度、转角方程及最大挠度和转角,EI为常数。解:1、弯矩方程为:qlx-qx?M(x)= 922L代入微分方程并积分得yql9Elw"-+x22gr2EI0(x) =一(2x -31)+C6#Elw(x)(x - 2)+ Cx+ D24
例5-2 图示简支梁受分布力作用,确定其挠度、转 角方程及最大挠度和转角,EI为常数。 解:1、弯矩方程为: 2 2 2 ( ) x q x ql M x = − 代入微分方程并积分得 x l Cx D qx EIw x x l C qx EI x = − + + = − + ( 2 ) 24 ( ) (2 3 ) 6 ( ) 3 2 y 2 2 2 " x q x ql EIw = − +