第五章梁弯曲时的位移S5-1梁的位移一挠度及转角B桥式吊梁在自重及重量作用下发生弯曲变形研究范围:等直梁在对称弯曲时位移的计算。研究目的:①对梁作刚度校核:②解超静定梁(变形几何条件提供补充方程)
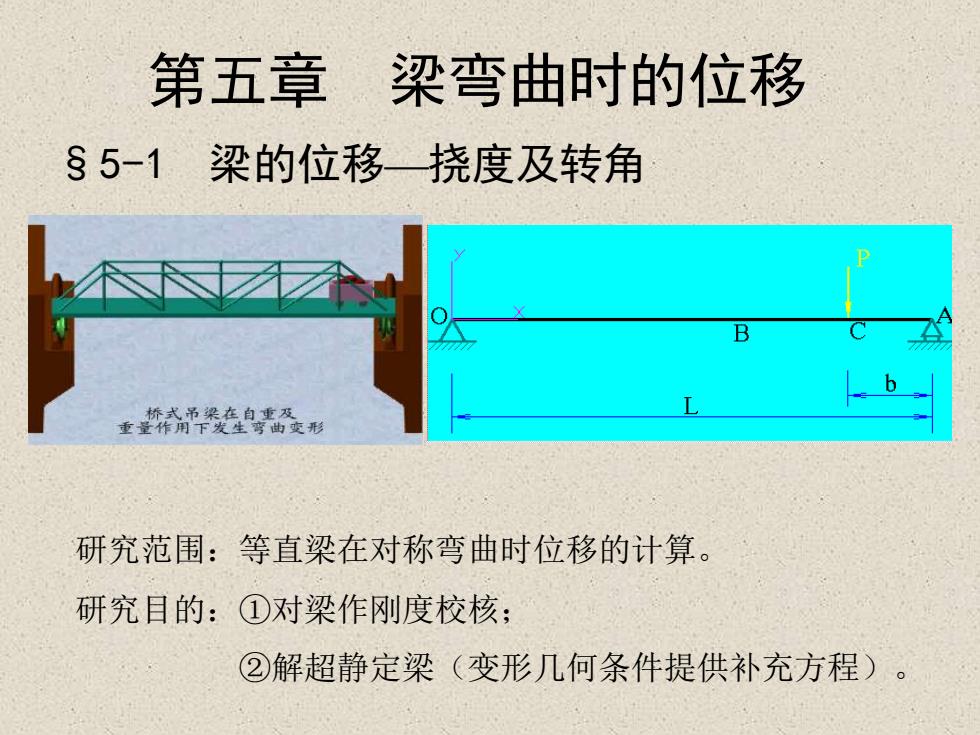
第五章 梁弯曲时的位移 §5-1 梁的位移—挠度及转角 研究范围:等直梁在对称弯曲时位移的计算。 研究目的:①对梁作刚度校核; ②解超静定梁(变形几何条件提供补充方程)
一、度量梁变形的两个基本位移量1.挠度:横截面形心沿垂直于轴线方向的线位移。用w表示。与y同向为正,反之为负。K2.转角:横截面绕其中性轴转X动的角度。用表示,顺时针转动为正,反之为负。二、挠曲线:变形后,轴线变为光滑曲线,该曲线称为挠曲线。其方程为:w=f (x)三、转角与挠曲线的关系:θ~tanQ=w=f'(x)小变形
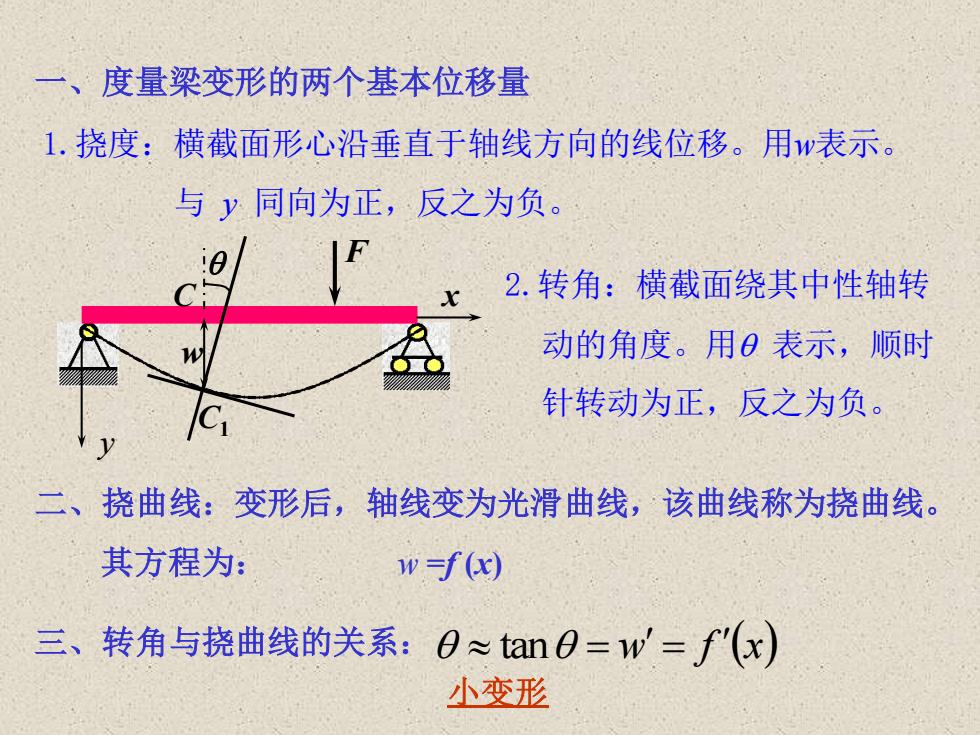
1.挠度:横截面形心沿垂直于轴线方向的线位移。用w表示。 与 y 同向为正,反之为负。 2.转角:横截面绕其中性轴转 动的角度。用 表示,顺时 针转动为正,反之为负。 二、挠曲线:变形后,轴线变为光滑曲线,该曲线称为挠曲线。 其方程为: w =f (x) 三、转角与挠曲线的关系: 一、度量梁变形的两个基本位移量 F x w C C1 y tan = w = f (x) 小变形

S5-2梁的挠曲线近似微分方程及其积分一、挠曲线近似微分方程M(x)1p(x)EIw"1+p(x)(1 + w2 )因为在小变形情况下:w<<11+w2~11M(x)~±"所以:w"~p(x)EI
§5-2 梁的挠曲线近似微分方程及其积分 一、挠曲线近似微分方程 ( ) ( ) EI M x x = 1 ( ) ( ) 2 3 2 1 1 w w x + = 因为在小变形情况下: wl 1 1 2 + w 所以: ( ) w x 1 ⇒ ( ) EI M x w

对于本书采用的坐标系,由下图可见:XVVM>0, w"<0MK0, w">0yM(x)即:hEI对等直梁:EIw" =-M(x)此即为挠曲线的近似微分方程
( ) EI M x 即: w = − EIw = −M(x) 对于本书采用的坐标系,由下图可见: M M>0, w″<0 x y M M<0, w″>0 x y 对等直梁: 此即为挠曲线的近似微分方程

二、求挠曲线方程(弹性曲线)1.微分方程的积分Elw"(x) = -M(x)EIw'(x)= [(-M(x)dx +C)EIw(x) = f (-M(x)dx Jix + C;x + D,C、D,为常数,由梁的边界条件(包括位移约束和连续条件)确定。常数CI、D,确定后,代入上两式即可分别得到梁转角方程和挠曲线方程,从而可确定任一截面的转角和度
二、求挠曲线方程(弹性曲线) EIw"(x) = −M (x) d 1 EIw'(x) = (−M (x)) x +C d d 1 1 EIw(x) = (−M (x)) x x +C x + D 1.微分方程的积分 C1、D1为常数,由梁的边界条件(包括位移约 束和连续条件)确定。 常数C1、D1确定后,代入上两式即可分别得到 梁转角方程和挠曲线方程,从而可确定任一截面的 转角和挠度