§5-7分子碰撞和平均自由程 一、分子碰撞的研究。 a.频繁地与其它分子相 碰撞,分子的实际运动 路径是曲折无规的。 b.正是碰撞,使得气体分 子能量按自由度均分。 ℃在气体由非平衡态过渡到平衡态中起关键作用。 d.气体速度按一定规律达到稳定分布。 .利用分子碰撞,可探索分子内部结构和运动规律。 子元道回退华
上页 下页 返回 退出 a.频繁地与其它分子相 碰撞,分子的实际运动 路径是曲折无规的。 b.正是碰撞,使得气体分 子能量按自由度均分。 c.在气体由非平衡态过渡到平衡态中起关键作用。 d.气体速度按一定规律达到稳定分布。 e.利用分子碰撞,可探索分子内部结构和运动规律。 §5-7分子碰撞和平均自由程 一、分子碰撞的研究

二、平均碰撞频率 单位时间内一个分子和其它分子碰撞的平均次数。 三、平均自由程刀公式 每两次连续碰撞之间一个分子自由运动的平均路程。 设分子的平均速率为下,则 (1)假定每个分子都是直径为d的刚性小球; (2)假定一个A分子以相对速率山运动,其他分子都静 止不动; 当A分子与其他分子作一次弹性碰撞 时,两个分子的中心相隔距离就是d。 江觉子觉道司退此
上页 下页 返回 退出 每两次连续碰撞之间一个分子自由运动的平均路程。 单位时间内一个分子和其它分子碰撞的平均次数。 . v Z = d (1)假定每个分子都是直径为d 的刚性小球; (2)假定一个A分子以相对速率 u 运动,其他分子都静 止不动; d 当A分子与其他分子作一次弹性碰撞 时,两个分子的中心相隔距离就是d。 设分子的平均速率为 v ,则 二、平均碰撞频率 Z 三、 平均自由程 公式
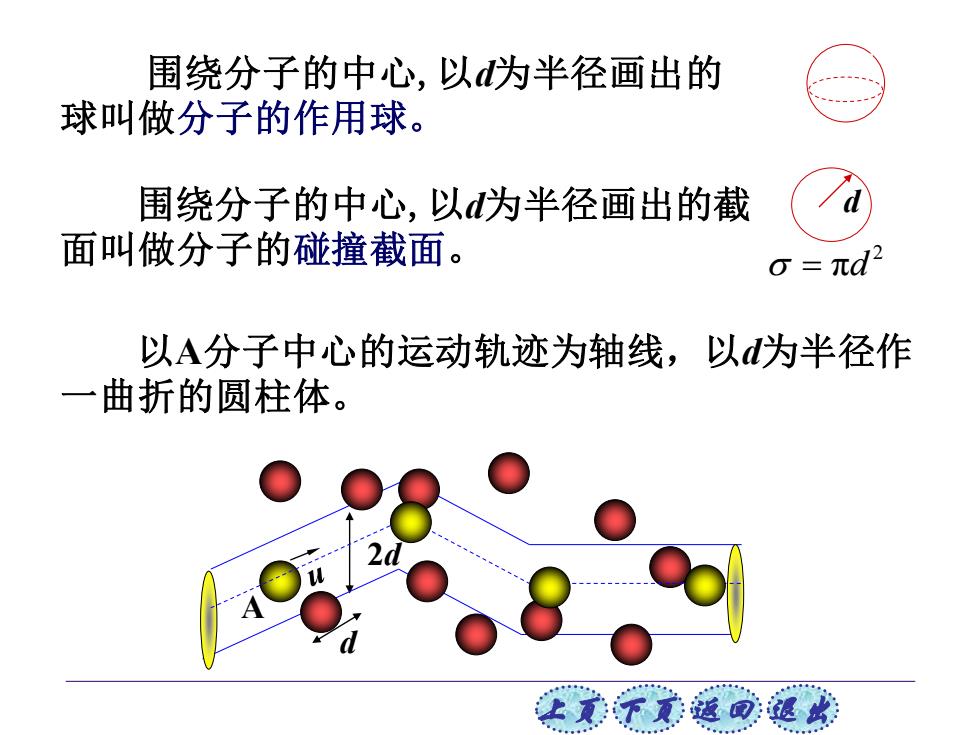
围绕分子的中心,以为半径画出的 球叫做分子的作用球。 围绕分子的中心,以d为半径画出的截 面叫做分子的碰撞截面。 =πd2 以A分子中心的运动轨迹为轴线,以d为半径作 一曲折的圆柱体。 上贰不觉返退此
上页 下页 返回 退出 围绕分子的中心,以d为半径画出的 d 球叫做分子的作用球。 d 2d A 围绕分子的中心,以d为半径画出的截 面叫做分子的碰撞截面。 以A分子中心的运动轨迹为轴线,以d为半径作 一曲折的圆柱体。 d 2 = πd
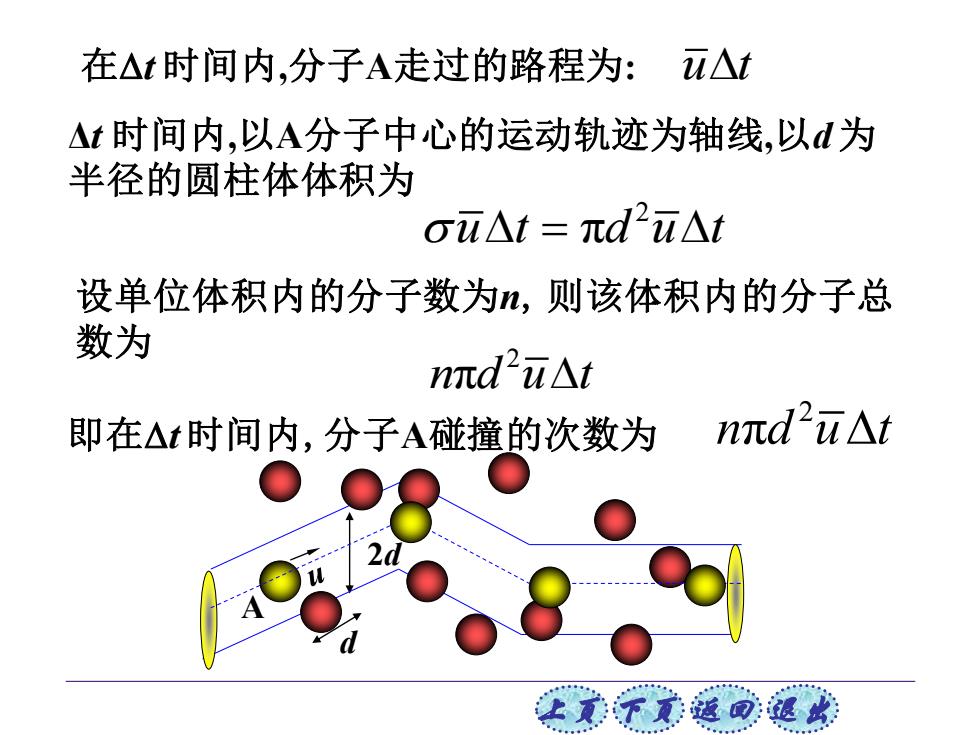
在△t时间内,分子A走过的路程为: u△t △t时间内,以A分子中心的运动轨迹为轴线,以d为 半径的圆柱体体积为 ou△t=πdu△t 设单位体积内的分子数为,则该体积内的分子总 数为 md2u△t 即在△t时间内,分子A碰撞的次数为 nπd2u△t 让美觉返司退
上页 下页 返回 退出 在t 时间内,分子A走过的路程为: Δt 时间内,以A分子中心的运动轨迹为轴线,以d 为 半径的圆柱体体积为 设单位体积内的分子数为n, 则该体积内的分子总 数为: 即在t 时间内,分子A碰撞的次数为 u t 2 u t d u t = π 2 n d u t π 2 n d u t π d 2d A
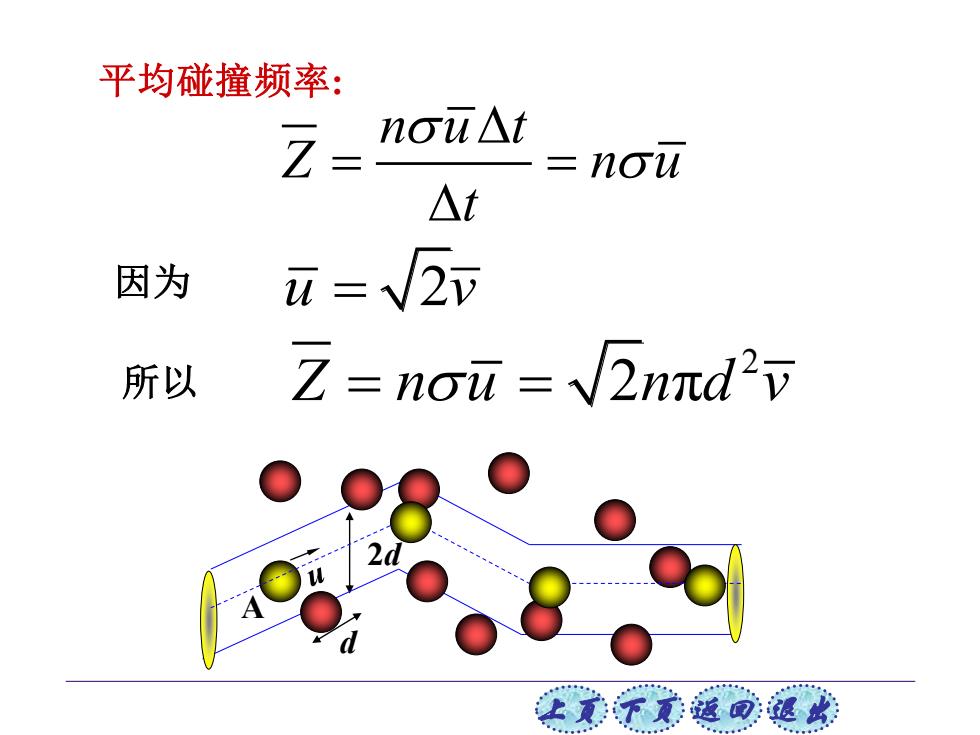
平均碰撞频率: Z= nou△t nou △t 因为 u=√2v 所以 Z=nou=√2nπd2v 上贰不觉返退此
上页 下页 返回 退出 平均碰撞频率: n u t Z n u t = = u v = 2 2 Z n u n d v = = 2 π d 2d A 因为 所以