
3.3闭环系统的稳定性ni +(n-n, )/2niA,e-Prt +g(t)=ZEB,e-t sin(o,t +β,), t ≥0=1I=n; +1Al=1,2,,n)为常数或关的多项式B,(l =n+1, ni+2,·, (n-n)/2)为常数。Aje-Pit和Bre-oit sin(it+β,)为两种类型的响应e-Pit(I = 1,2,. n,)和e-(o}jo)(I = n, +1, n, + 2,,n, +(n-n,)/2)被称为系统的运动模态或者共轭复模态;T(s)的单位脉冲相应函数(t)则有两类运动模态线性叠加而成
3.3 闭环系统的稳定性 ( ) ( ) sin( ), 0 2 1 1 1 1 1 1 = + + + − = + − = − g t A e B e t t n n n l n l l t l n l p t l l l 为常数。 ( )为常数或关于的多项式 ( 1, 2, , ( ) 2) 1,2, , , 1 1 1 1 B l n n n n A l n t l l = + + − = Al e − pl t 和Bl e − l t sin(l t + l )为两种类型的响应; 的单位脉冲相应函数 则有两类运动模态线性叠加而成。 被称为系统的运动模态或者共轭复模态; 和 T(s) g(t) ( 1,2,., ) ( 1, 2,., ( )/ 2) 1 1 1 1 ( ) e l n1 e l n n n n n p t j t l l l = = + + + − − −
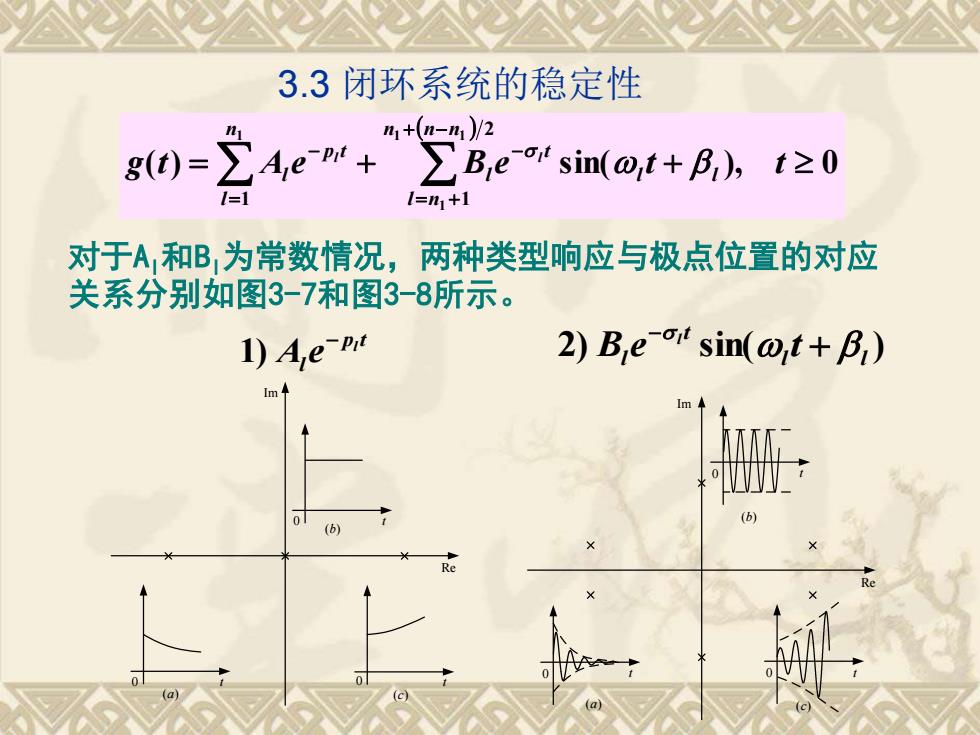
3.3闭环系统的稳定性ni+(n-n,)/2nZA,e-Pit +EB,e-it sin(,t + β,),t≥0g(t) =1=1[=n;+1对于A,和B,为常数情况,两种类型响应与极点位置的对应关系分别如图3-7和图3-8所示2) B,e-oit sin(o,t + β,)1) A,e-PitIm(bbRe
3.3 闭环系统的稳定性 ( ) ( ) sin( ), 0 2 1 1 1 1 1 1 = + + + − = + − = − g t A e B e t t n n n l n l l t l n l p t l l l 对于Al和Bl为常数情况,两种类型响应与极点位置的对应 关系分别如图3-7和图3-8所示。 p t l l A e − 1) 2) sin( ) l l t l B e t l + − Im 0 t 0 t 0 t Re (a) (b) (c) Im Re 0 t 0 t 0 t (a) (b) (c)

3.3闭环系统的稳定性g(t)存在上界的充分必要条件:ni+(n-n)/2-pit +> g(t)dt = JoB,e-oit sin(o,t + β) dt ≤M (3-22)EAe1-1(=n)+1当t→时,有e-pit →0,e-α →0即,系统的闭环传递函数极点均具有负实部。闭环系统稳定性的充分必要条件:系统的闭环特征方程n+(n-n)/2A(s)=II(s+ p)) II(s+o,- jo,)(s+o,+ jo,)=0 (3-23)[=[=n,+]的根- p,(l = 1,., n,),-o, ± jo,(l = n, + 1,., n, + (n-n,)/2)在左半s平面
3.3 闭环系统的稳定性 g(t)存在上界的充分必要条件: ( ) ( ) sin( ) (3- 22) 0 2 1 1 0 1 1 1 1 + − = + − = − g t dt = A e + B e t + dt M n n n l n l l t l n l p t l l l t → → 0, → 0 − p t − l e e 当 时,有 l 即,系统的闭环传递函数极点均具有负实部。 闭环系统稳定性的充分必要条件: ( ) ( ) 在左半 平面。 的 根 ( ) 系统的闭环特征方程 s p l n j l n n n n s s p s j s j l l l n n n l n l l l l n l l 1,., , ( 1,., 2) ( ) ( ) ( )( ) 0 (3 - 23) 1 1 1 1 2 1 1 1 1 1 1 − = − = + + − = + + − + + = + − = = +