
c=c1;if (c==0)c=c2; if(c&1==1){y=y0+(y2-y0)*(x1-x0)/(x2-x0);x=x1;} else if(c&2==2){y=y0+(y2-y0)*(xr-x0)/(x2-x0); x=xr; else if(c&4==4){x=x0+(x2-x0)*(yb-y0)/y2-y0); y=yb; else if(c&8==8){x=x0+(x2-x0)*(yt-y0)/(y2-y0); y=yt; if (c==c1) {x0=x;y0=y;makecode(x,y,c1);} else {x2=x;y2=y;makecode(x,y,c2);} showline(x0,y0,x2,y2);∥显示可见线段
c=c1; if (c==0) c=c2; if (c&1==1){y=y0+(y2-y0)*(x1-x0)/(x2-x0); x=x1;} else if (c&2==2){y=y0+(y2-y0)*(xr-x0)/(x2-x0); x=xr;} else if (c&4==4){x=x0+(x2-x0)*(yb-y0)/(y2-y0); y=yb;} else if (c&8==8){x=x0+(x2-x0)*(yt-y0)/(y2-y0); y=yt;} if (c==c1) {x0=x; y0=y; makecode(x, y, c1);} else {x2=x; y2=y; makecode(x, y, c2);} } showline(x0, y0, x2, y2); //显示可见线段}
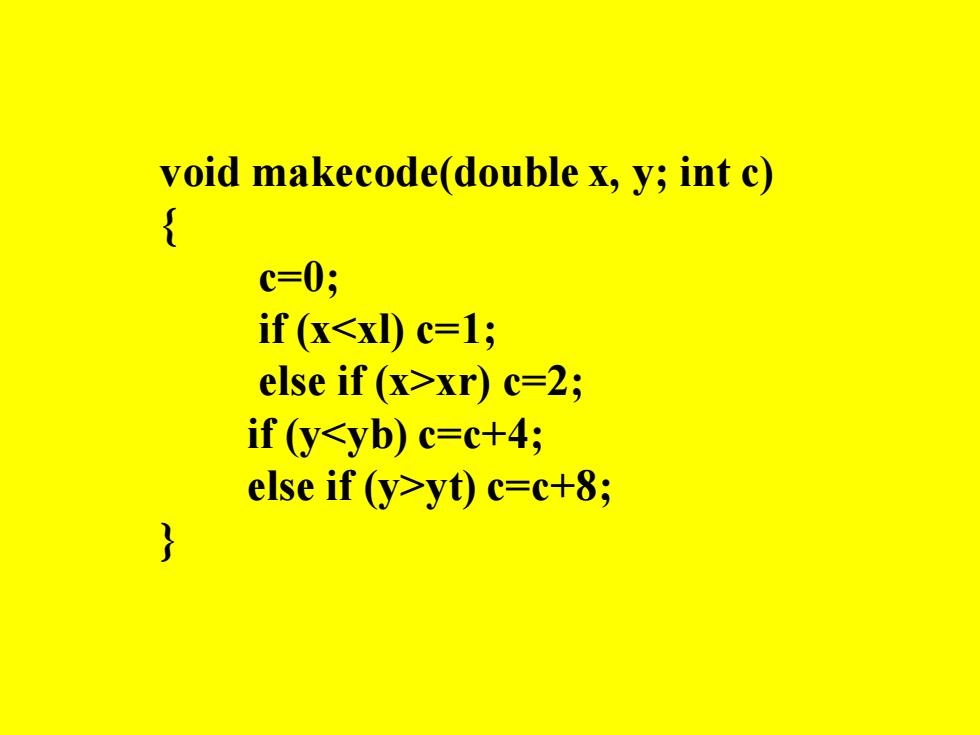
void makecode(double x,y;int c) c=0; if (x<xl)c=1; else if (x>xr)c=2; if (y<yb)c=c+4; else if (y>yt)c=c+8;
void makecode(double x, y; int c) { c=0; if (x<xl) c=1; else if (x>xr) c=2; if (y<yb) c=c+4; else if (y>yt) c=c+8; }

中点分割算法 设要裁剪的直线段为0。中点分割算法 的基本思想如下:可分成两个过程平行进行, 即从0点出发找出离点0最近的可见点,和从 P点出发找出离点P最近的可见点。这两个 最近可见点的连线就是原直线段的可见部分。 从出发找最近可见点的方法是先求的0中 中点。重复上过程,直到长度小于给定的小数 为止
设要裁剪的直线段为 。中点分割算法 的基本思想如下:可分成两个过程平行进行, 即从 点出发找出离点 最近的可见点,和从 点出发找出离点 最近的可见点。这两个 最近可见点的连线就是原直线段的可见部分。 从 出发找最近可见点的方法是先求的 中 点 ,若 不能定为显然不可见,则取 代替,否则取 代替,再对新的求 中点。重复上过程,直到长度小于给定的小数 为止。 P1 0 P m P m P P0 1 P m P 0 1 P P 0 P P1 0 P 0 1 P P m P P0 中点分割算法

Po A 卫 B 图3.27 中点分割薛法

P是否可见? P=P exit PP显然不可见? 原线完全不可见 香 exit P.=(p6+p)/2 pa-pl<8? Po=Px exit PP显然不可见? 是 Po=P P=P 图3.28中点分割算法框图