
=-3 =9 X=-2 因此方程组有唯一解,这个结果和消元法一致! 定义满足下列两个条件的矩阵称为行阶梯矩阵,简称阶梯形。 (1)若有零行,则零行位于非零行的下方: (2)每个首非零元(非零行从左边数起第一个不为零的元)前面零的个数 逐行增加。 2-3 9 -3 9 0 04 0 01 0 1 1 4 0 0 0 0 0032 0 0 0 首非零元为1,且首非零元所在列的其它元都为零的梯矩阵, 称为行最简形 矩阵,简称最简形。 [1 04 07 0 12 0 0 00 问题:是否每个矩阵都可以经过初等行变换化为行阶梯矩阵呢? 定理任意m×n矩阵A总可以经初等行变换化为阶梯形矩阵及行最简形矩 阵。 证明Step1若A的元全为0,A已经是一个阶梯矩阵。 Step2设非零矩阵A的第i列是自左而右的第一个非零列,设a,≠0 (否则,若a非零,作行变换片分,总可使第j列的第一个元非零),矩阵 A的各行分别作行变换:5+(-r=2,3,m 0…0a …☑n 得到: 0.0 A→ 0 B : 0 …0 其中A1是(m-1)×(n-)矩阵,对施行上面同样的步骤,如此下去,即可得 梯矩阵。 24
24 x x x ⎧ ⎪ ⎨ ⎪ ⎩ 1 2 3 =-3 =9 =-2 因此方程组有唯一解,这个结果和消元法一致! 定义 满足下列两个条件的矩阵称为行阶梯矩阵,简称阶梯形。 (1)若有零行,则零行位于非零行的下方; (2)每个首非零元(非零行从左边数起第一个不为零的元)前面零的个数 逐行增加。 123 004 000 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ 0 2 -3 9 00 1 4 0 0 0 32 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ 1 1 -3 9 01 1 4 00 0 1 首非零元为 1,且首非零元所在列的其它元都为零的梯矩阵,称为行最简形 矩阵,简称最简形。 1040 0120 0001 ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 问题:是否每个矩阵都可以经过初等行变换化为行阶梯矩阵呢? 定理 任意m n × 矩阵 A 总可以经初等行变换化为阶梯形矩阵及行最简形矩 阵。 证明 Step1 若 A 的元全为 0, A 已经是一个阶梯矩阵。 Step2 设非零矩阵 A 的第 j1 列是自左而右的第一个非零列,设 1 0 j a ≠ (否则,若 1 ij a 非零,作行变换 1 i r r ↔ ,总可使第 j1 列的第一个元非零),矩阵 A 的各行分别作行变换: 1 1 1 1 ( ) , 2,3,..., . ij i j a r ri m a +− = 得到: 1 1 1, 1 1 1 1 0 0 , 0 00 0 00 j j n A B A ⎛ ⎞ aa a + ⎜ ⎟ → = ⎝ ⎠ " " " #"# # " 其中 A1 是( )( ) 1 m nj −1 × − 矩阵,对施行上面同样的步骤,如此下去,即可得 梯矩阵

继续对行阶梯矩阵做行变换: 每个非零行同除以该行的首非零元,就可以将该行的首非零元化为1。 再利用矩阵的初等行变换(3),将首非零元所在列的其他元素化为零,就得到 最简形。 证毕。 推论 m×n矩阵A经过初等行变换化成的行最简形矩阵是唯一的。 例用初等行变换将矩阵A化成行阶梯矩阵和最简形。 4-122 -1-6 A= -1 -1 6 2 -2 0 0 解: -1 -1 6 2 1 -6-2 A53 0 -4 12 4 -1 2→ 0 -4 12 4 =B 0 4 -12 2 4-2 0 0 0 6 -4 12 4 0 0 0 [11-6 「10 -3 0 0 1 -3 -1 烧 0 1 -3 0 0 0 0 1 乃-5 =C 0 0 0 0 0 0 0 0 B是所求的梯矩阵,C是最简形。 3.初等矩阵的概念 2)定义 由单位矩阵E经过一次初等变换而得到的方阵称为初等矩阵。 100 104 万+45 E=010 0 1 0 001 001 三种初等变换对应着三种初等矩阵。 1.5)r(或c,→c) 25
25 继续对行阶梯矩阵做行变换: 每个非零行同除以该行的首非零元,就可以将该行的首非零元化为 1。 再利用矩阵的初等行变换(3),将首非零元所在列的其他元素化为零,就得到 最简形。 证毕。 推论 m n × 矩阵 A 经过初等行变换化成的行最简形矩阵是唯一的。 例 用初等行变换将矩阵 A 化成行阶梯矩阵和最简形。 A ⎡ − ⎤ ⎢ ⎥ − − = ⎢ ⎥ ⎢− − ⎥ ⎢ ⎥ ⎣ − ⎦ 0 4 12 2 3 1 62 1162 2 200 解: A B ↔ + + − + ⎡ ⎤⎡ ⎤ ⎢ ⎥⎢ ⎥ − − ⎯⎯⎯→ ⎯⎯⎯→ = ⎣ ⎦⎣ ⎦ − 1 3 2 4 2 -1r r r r r 1 1 -6 -2 0 4 12 4 00 0 6 00 0 0 1 3 2 1 4 1 r r r 3r r 2r -1 -1 6 2 0 4 12 4 0 4 -12 2 0 4 12 4 3 1 3 1 2 2 r r r r r C + + − ⎡ ⎤⎡ ⎤ − − ⎢ ⎥⎢ ⎥ ⎯⎯→ ⎯⎯⎯→ = ⎣ ⎦⎣ ⎦ 2 2 3 r r - 4 r 6 11 6 2 10 30 0 1 -3 -1 0 1 -3 0 00 0 1 00 0 1 00 0 0 00 0 0 B 是所求的梯矩阵,C 是最简形。 3. 初等矩阵的概念 2) 定义 由单位矩阵 E 经过一次初等变换而得到的方阵称为初等矩阵。 1 3 4 100 104 010 ~ 010 001 001 r r E + ⎛ ⎞⎛ ⎞ ⎜ ⎟⎜ ⎟ = ⎝ ⎠⎝ ⎠ 三种初等变换对应着三种初等矩阵。 1. ( ) ij i j rr cc ↔ ↔ 或
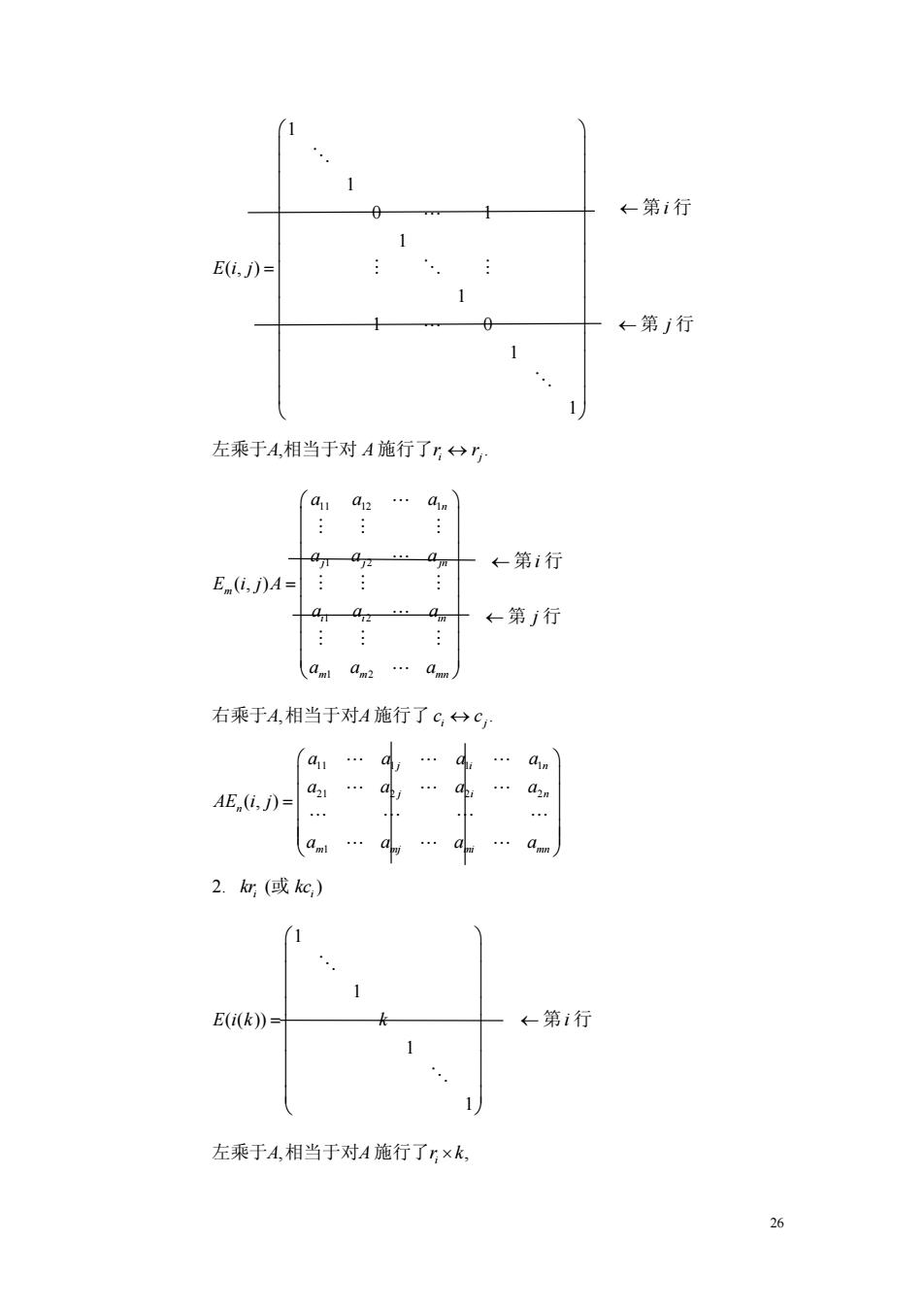
←第i行 E6,)= ←第j行 左乘于A,相当于对A施行了,)r a11 a ain ←第i行 E(i,j)A= ←第j行 am2 右乘于A,相当于对A施行了C,分C, … AE,(i,j)= … 2.a(或kc) E(i(k)) ←第i行 左乘于A,相当于对A施行了,×k, 26
26 1 1 0 1 1 (, ) 1 1 0 1 1 Ei j ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ % " #%# " % , . 左乘于 相当于对 施行了 A A rr i j ↔ 11 12 1 1 2 1 2 1 2 (, ) n j j jn m i i in m m mn aa a aa a E ijA aa a aa a ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ " ## # " ## # " ## # " , . 右乘于 相当于对 施行了 A A cc i j ↔ 11 1 1 1 21 2 2 2 1 (, ) jin jin n m mj mi mn aaaa aaaa AE i j aaaa ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ """ """ """" """ 2. ( ) i i kr kc 或 1 1 ( ( )) 1 1 Eik k ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ % % , , 左乘于 相当于对 施行了 A A rk i × ← 第 行i ← 第 行j ← 第 行i ← 第 行j ← 第 行i
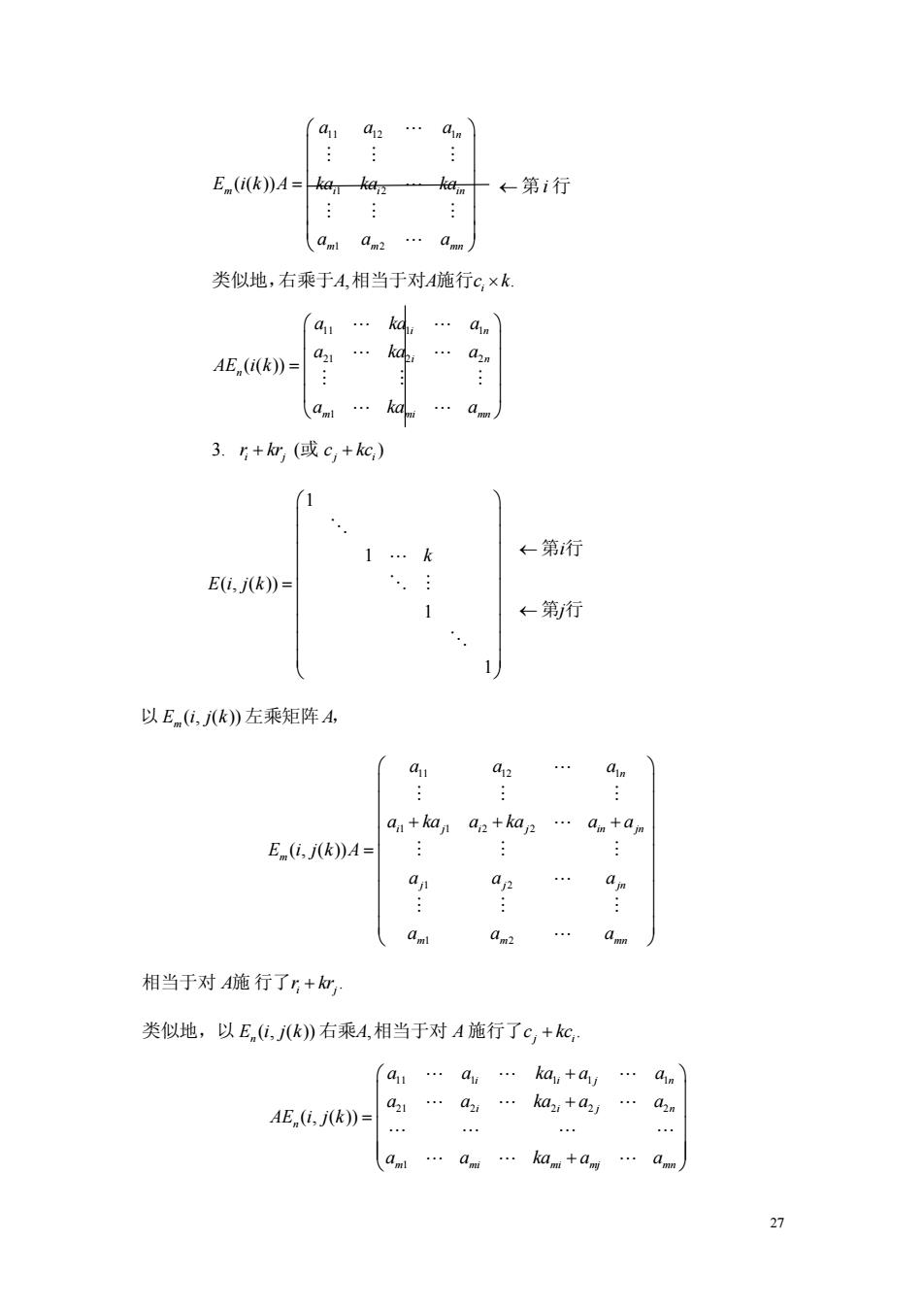
a a12 ain E(i(k))A=kai key ←第i行 、aml am2 amn 类似地,右乘于A,相当于对A施行c×k 4 … kau … AE,(i(k))= az kdpi aml 3.5+a(或c,+kc,) 1 …k ←第行 E(i,j(k))= 1 ←第行 以E(亿,k)》左乘矩阵A, 411 a2 … ain an+kan a2+ka2… ain+aim E(i.j(k))A= 0) ap aj dm am2 amn 相当于对A施行了,+: 类似地,以E,jk)右乘A,相当于对A施行了c,+kc a11…ai… ka,+a…an a21…a2,…ka2+a2j AE,(i,j(k)= a2n … … am…kanm+ang 27
27 11 12 1 1 2 1 2 ( ( )) n m i i in m m mn aa a E i k A ka ka ka aa a ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ " ## # " ## # " 类似地, , . 右乘于 相当于对 施行 A A ck i × 11 1 1 21 2 2 1 ( ( )) i n i n n m mi mn a ka a a ka a AE i k a ka a ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ " " " " ### " " 3. ( ) ij ji r kr c kc + + 或 1 1 ( , ( )) 1 1 k Ei jk ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ % " % # % ( , ( )) 以 左乘矩阵 , E i jk A m 11 12 1 1 12 2 1 2 1 2 ( , ( )) n i j i j in jn m j j jn m m mn aa a a ka a ka a a E i jk A aa a aa a ⎛ ⎞ ⎜ ⎟ ++ + = ⎝ ⎠ " ## # " ## # " ## # " . A i j 相当于对 施 行了r kr + ( , ( )) , . En ji 类似地,以 右乘 相当于对 施行了 i j k A A c kc + 11 1 1 1 1 21 2 2 2 2 1 ( , ( )) i ij n i ij n n m mi mi mj mn a a ka a a a a ka a a AE i j k a a ka a a ⎛ ⎞ + ⎜ ⎟ + = + ⎝ ⎠ "" " "" " "" " " "" " ← 第 行i ← 第 行i ← 第 行j

E(i,i)E(i(k),E(i,i(k) 左乘行变,右乘列变 1 02-1 例 设A= 4 -25 3 求E(L,3)A,AE(L,3) 0 1 5 0011 02-1 0 12 5 解 E(L,3)A= 0 0 4 -2 5 3 4 -25 3 10 0八012 5 1 02-1 (102 -1 1 3 5 4= 4-2 5 3 -25 3 0125 102 -1 0 0 0 1 0 1 -1 2 01-1 0 1 00 AE(1,3)= 4-2 3 5 -24 012 0 5)八0 2 10 5 0 0 1 102 2 01 1 4= 4-25 3 919 5 -243 012 2 10 定理设A是一个m×n矩阵,对A施行一次初等行变换,相当于在A的 左边乘以一个相应的m阶初等矩阵;对A施行一次初等列变换,相当于在A的 右边乘以一个相应的n阶初等矩阵。 由定理,可知: E(i,j)E(i,j)=E, E(kE(i2》=E, E(i,i(k))E(i,j(-k=E 初等矩阵均是可逆矩阵,且其逆矩阵还是初等矩阵。具体地,有: E(i,j)=E(,j), E(》=E(》 28
28 E( , ), ( ( )), ( , ( )) i j Eik Ei jk 左乘行变 右乘列变 , 例 102 1 4 25 3, 0125 A ⎛ ⎞ − ⎜ ⎟ = − ⎜ ⎟ ⎝ ⎠ 设 求 E A AE (1,3) , (1,3). 解 001 1 0 2 1 0 1 2 5 (1,3) 0 1 0 4 2 5 3 4 2 5 3 100 0 1 2 5 1 0 2 1 E A ⎛ ⎞⎛ ⎞ ⎛ ⎞ − ⎜ ⎟⎜ ⎟ ⎜ ⎟ = − =− ⎝ ⎠⎝ ⎠ ⎝ ⎠ − 1 3 102 1 0125 4 25 3 4 25 3 0125 102 1 r r A ↔ ⎛ ⎞⎛ ⎞ − ⎜ ⎟⎜ ⎟ = − ⎯⎯⎯→ − ⎝ ⎠⎝ ⎠ − 0010 102 1 201 1 0100 (1,3) 4 2 5 3 5 2 4 3 1000 0125 2105 0001 AE ⎛ ⎞ ⎛⎞ ⎛⎞ − − ⎜ ⎟ ⎜⎟ ⎜⎟ ⎜ ⎟ =− =− ⎜ ⎟ ⎝⎠ ⎝⎠ ⎜ ⎟ ⎝ ⎠ 1 3 102 1 201 1 4 25 3 5 24 3 0125 2105 c c A ↔ ⎛ ⎞⎛ ⎞ − − ⎜ ⎟⎜ ⎟ = − ⎯⎯⎯→ − ⎝ ⎠⎝ ⎠ 定理 设 A 是一个m n × 矩阵,对 A 施行一次初等行变换,相当于在 A 的 左边乘以一个相应的 m 阶初等矩阵;对 A 施行一次初等列变换,相当于在 A 的 右边乘以一个相应的 n 阶初等矩阵。 由定理,可知: E(, ) (, ) , i jEi j E = 1 E( ( )) ( ( )) , ik Ei E k = Ei jk Ei j k ( , ( )) ( , ( )) E. − = 初等矩阵均是可逆矩阵,且其逆矩阵还是初等矩阵。具体地,有: 1 Ei j Ei j ( , ) ( , ), − = 1 1 Eik Ei ( ( )) ( ( )), k − =