内蒙古科技大学：《材料力学》课程PPT教学课件（土木类）第七章 应力状态和强度理论

7×106M.-35.7MPaWp元×1003y16a图示斜截面上应力分量为：t.R30,+00.-0cos(-60 )-t, sin(-60°)十30°22= 16.9MPa9.-0sin 2α + t, cos2α = -45.4MPaT-30°2

( ) ( ) 16.9MPa cos 60 sin 60 2 0 2 0 3 0 = − − − − + + = −    x x x     sin 2 cos 2 45.4MPa 2 0 3 0 + = − − = − a  a   x x  图示斜截面上应力分量为： 35.7MPa 100 16 π 7 10 3 6 P e = −   = = − W M x  C x  x x x  x  y y y 30° n   -30 -30° °

2、应力圆由任一斜截面上应力分量的计算公式可得：O,+o,Ox-o,cos 2α - t, sin 2α0a22Ox-oysin 2α+t,cos2αTO2两式两边平方后求和可得：o.to)+.-(o0) +.a2

2、应力圆 由任一斜截面上应力分量的计算公式可得： a  a      a cos 2 sin 2 2 2 x x y x y − − = + − a  a    a sin 2 cos 2 2 x x y + − = 两式两边平方后求和可得： 2 2 2 2 2 2 x x y x y        a a +         − + =         + −

而圆方程为：（x-a)+(y-b）=R可见前式实际上表示了在?为水平轴、为垂直轴的坐标系下的一个圆，其圆心坐标为：C+半径为：R如下图

而圆方程为： ( ) ( ) 2 2 2 x − a + y − b = R 可见前式实际上表示了在为水平轴、为垂直轴 的坐标系下的一个圆，其圆心坐标为：         + , 0 2  x  y 半径为： 2 2 2 x x y R    +         − = 如下图

To单元体斜截面上应力（α，tα）和应力圆上点的坐标（α，α）一一对应，因此可通过确定应力圆上相应点的坐标来求斜截面上应力（αα，tα）。因为圆心一定在轴上，只要知道应力圆上的两点（即单元体两个面上的应力），即可确定应力圆

单元体斜截面上应力（a，a）和应力圆上点的 坐标（a，a）一一对应，因此可通过确定应力圆上 相应点的坐标来求斜截面上应力（a，a）。 因为圆心一定在轴上，只要知道应力圆上的两 点（即单元体两个面上的应力），即可确定应力圆。   O C 2 2 2 x x y    +         + 2  x + y ( , ) a a   2 2 2 x x y    +         −

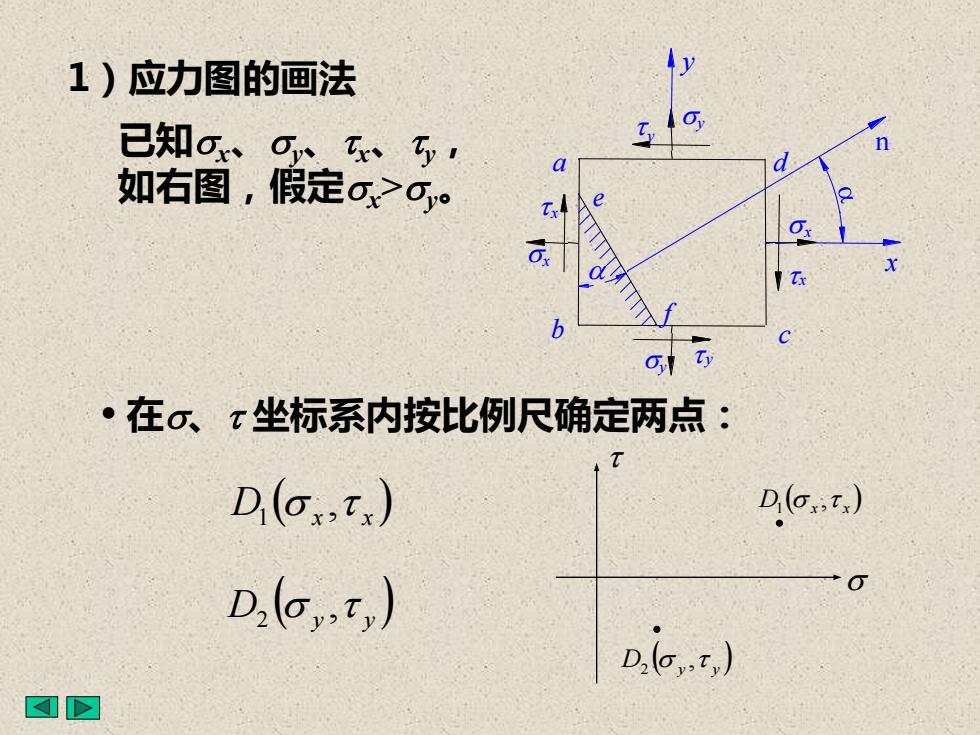
1）应力图的画法O,已知oyTx、Tya如右图，假定o>0%。a.Tyo·在o、T坐标系内按比例尺确定两点：TD(or,t.)D(or,t.)6D,(o,t,)D,(o,t,)

1）应力图的画法 ( ) D x x  , 1 ( ) D y y  , 2 已知x、y、x、y， 如右图，假定x>y。 • 在、 坐标系内按比例尺确定两点：   ( ) D x x  , 1 ( ) D y y  , 2 a d b c e f a x  y  x x n x x y y  y y