
·连接D、D,两点,线段D,D,与o轴交于C点。2D(o,t.)OD,(oy,t,)·以C为圆心,线段CD,或CD,为半径作圆,即为应力圆。TDot)6
• 以C为圆心,线段CD1或CD2为半径作圆,即为应 力圆。 • 连接D1、D2两点,线段D1D2与轴交于C点。 ( ) D x x , 1 ( ) D y y , 2 C ( ) D x x , 1 ( ) D y y , 2 C
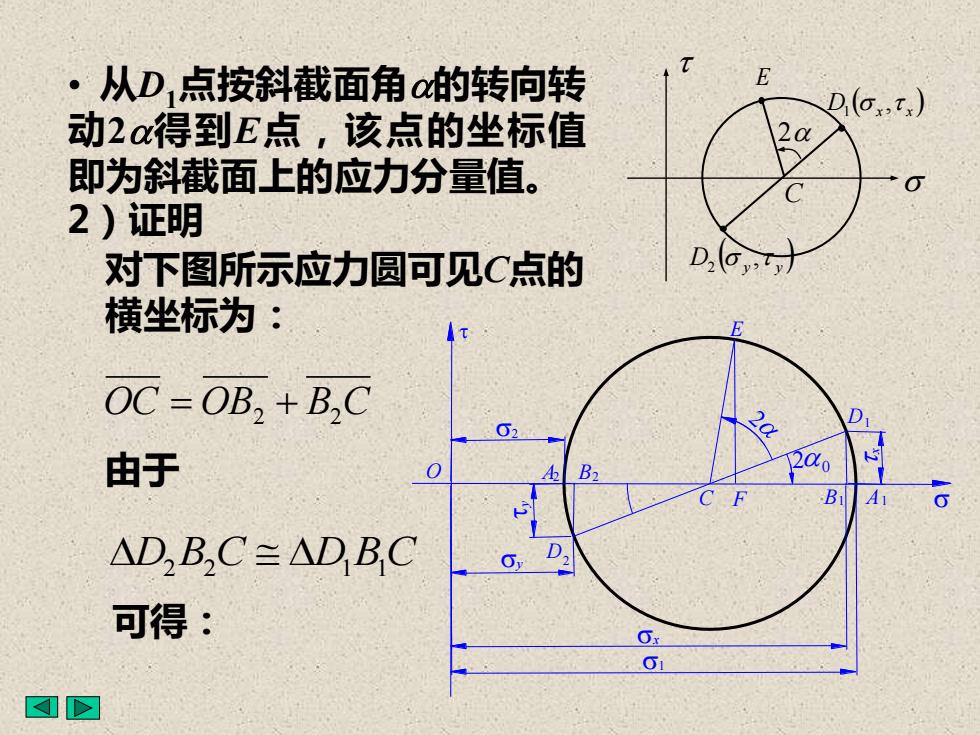
E·从D,点按斜截面角α的转向转(o.,t.动2α得到E点,该点的坐标值即为斜截面上的应力分量值。O2)证明D,(o对下图所示应力圆可见C点的横坐标为:ITOC = OB, + B,C020.由于YBAAD,B,C= AD,B,C可得:O0
2)证明 对下图所示应力圆可见C点的 横坐标为: • 从D1点按斜截面角a的转向转 动2a得到E点,该点的坐标值 即为斜截面上的应力分量值。 ( ) D x x , 1 ( ) D y y , 2 C 2a E O C 2 F B1 A1 A2 B2 D1 D2 E x y y x 1 2a 0 OC = OB2 + B2 C 由于 D2 B2 C D1 B1 C 可得:

B,C= B,C则:dx-0ox+o,OC = OB, + B,B, / 2 = α,22因此,C点坐标为应力圆圆心坐标,并且B,B,+ B,D,CD,=T22该线段长度等于应力圆半径。从而证明上述圆确为应力圆
B2 C = B1 C 2 2 2 1 2 / 2 x y x y OC OB B B y + = − = + = + 因此,C点坐标为应力圆圆心坐标,并且 2 2 2 1 1 2 1 2 1 2 2 x x y B D B B CD + − + = = 该线段长度等于应力圆半径。从而证明上述圆 确为应力圆。 则:

另外,E点横坐标为:0= = OF = OC +CF = OC+CE cos(2α +2α0)= OC +CE cos2α.cos2α- CEsin 2α,sin 2α0,+0,+,-0cos2α-t,sin2α=0即: OE=22同理可得E点的纵坐标为:0,-0sin2α+t,cos2α=TaTB =EF-2可见,E点坐标值即为α斜截面上的应力分量值A
另外,E点横坐标为: a a a + = − = = sin 2 cos 2 2 x x y E EF ( ) a a a a a a cos 2 cos 2 sin 2 sin 2 cos 2 2 0 0 0 OC C E C E E OF OC C F OC C E = + − = = + = + + 可见,E点坐标值即为a斜截面上的应力分量值。 a a a − = − + + = cos 2 sin 2 2 2 x x y x y 即: E 同理可得E点的纵坐标为:

由于应力圆上点的坐标与单元体面上的应力分量值一一对应,因此,按比例作图,可通过直接用尺子量出坐标值来求任意斜截面上的应力分量,此即称为图解法。例7-2用图解法求图示α=-30°斜截面上的应力值。解:按一定比例画出应力圆。t=35.7MPa因为图示应力状态有:o,=63.7MPaQ,=63.7MPa>030°xng,=0T, = -t, =-35.7MPa
由于应力圆上点的坐标与单元体面上的应力分量 值一一对应,因此,按比例作图,可通过直接用尺子 量出坐标值来求任意斜截面上的应力分量,此即称为 图解法。 解:按一定比例画出应力圆。 x = 63.7MPa 0 y = 0 = − = −35.7MPa x y 例7-2 用图解法求图示a =−30°斜截面上的应力值。 因为图示应力状态有: x 30° x=35.7MPa x=63.7MPa y n