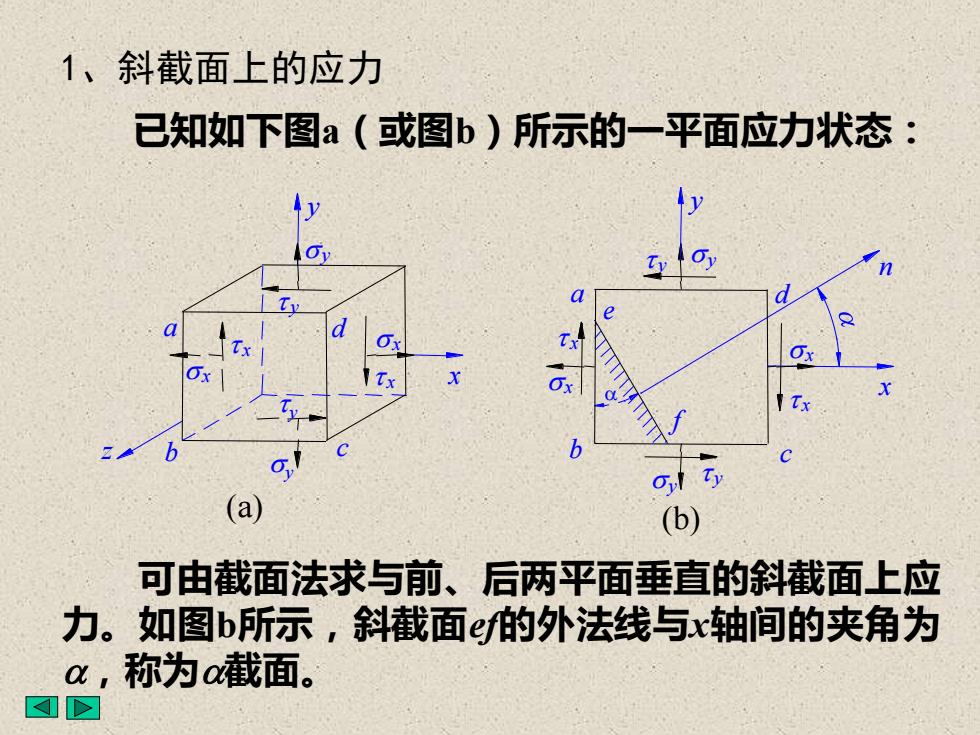
1、斜截面上的应力已知如下图a(或图b)所示的一平面应力状态:Oylty(a)(b)可由截面法求与前、后两平面垂直的斜截面上应力。如图b所示,斜截面e的外法线与x轴间的夹角为α,称为α截面。A
1、斜截面上的应力 已知如下图a(或图b)所示的一平面应力状态: e f a n x y z a b c d x y (a) x y y y x x a d b c x y x x (b) x x y y y y 可由截面法求与前、后两平面垂直的斜截面上应 力。如图b所示,斜截面ef的外法线与x轴间的夹角为 a,称为a截面

应力的正负和斜截面夹角的正负规定:1)正应力o拉为正,压为负;2)切应力使单元体产生顺时针旋转趋势为正:反之为负;3)对α角,x轴逆时针旋转这一角度而与斜截面外法线重合时,其值为正;反之为负。取图c所示分离体进行分析。图c中所示斜截面上应力和斜截面夹角均为正。(c)
应力的正负和斜截面夹角的正负规定: 1)正应力拉为正,压为负; 2)切应力使单元体产生顺时针旋转趋势为正;反之 为负; 3)对a角,x轴逆时针旋转这一角度而与斜截面外法 线重合时,其值为正;反之为负。 取图c所示分离体进行分析。图c中所示斜截面 上应力和斜截面夹角均为正。 e f b y x a a (c) x y
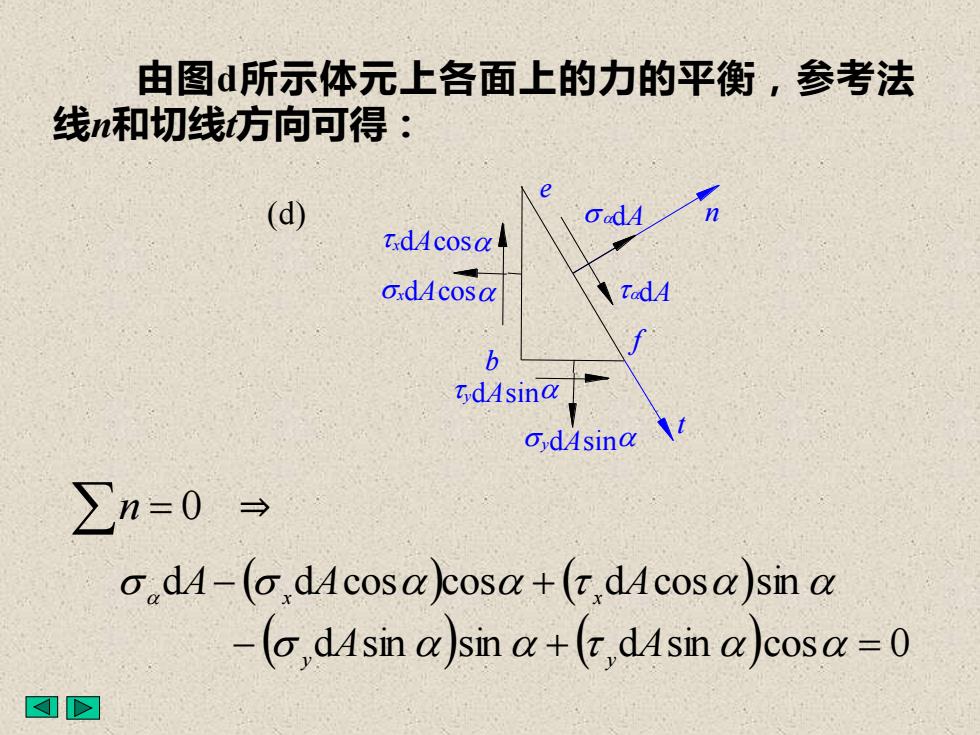
由图d所示体元上各面上的力的平衡,参考法线n和切线方向可得:(d)CadAt.dAcosαo.dAcosaTadAbtdAsinao,dAsinaIn=0 =o.dA-(o,dAcosα)cosα+ (t,dAcosα)sin α- (,dAsin α)sin α + (t,dAsin α)cosα = 0
n = 0 ( ) ( ) ( d sin )sin ( d sin )cos 0 d d cos cos d cos sin − + = − + a a a a a a a a a A A A A A y y x x 由图d所示体元上各面上的力的平衡,参考法 线n和切线t方向可得: ⇒ n t ydAsina (d) b f ydAsina adA xdAcosa e adA xdAcosa

Zt=0-t,dA-(α dAcosα)sin α-(t,dAcosα)cosα+ (α,dAsin α)cosα+ (t,dAsin α)sin α = 0其中dA为斜截面e的面积由此可得,任一斜截面上的应力分量为:O,+oyOx-oycos 2α-t, sin 2α0220x-0,sin 2α + t, cos 2α22
a a a cos 2 sin 2 2 2 x x y x y − − + + = 由此可得,任一斜截面上的应力分量为: t = 0 ( ) ( ) ( d sin )cos ( d sin )sin 0 d d cos sin d cos cos + + = − − a a a a a a a a a A A A A A y y x x ⇒ 其中dA为斜截面ef的面积。 a a a sin 2 cos 2 2 x x y + − =

例7-1图示圆轴中,已知:圆轴直径d-100mm,轴向拉力F=500kN,外力矩M.=7kN·m。求C点α=-30°截面上的应力。V口Ca.OT.7(a)(b)解:C点应力状态如图b所示,其拉应力和切应力为:F500×103=63.7MPax元A元×10024
解:C点应力状态如图b所示,其拉应力和切应力为: 63.7MPa 100 4 π 500 10 2 3 = = = A F x 例7-1 图示圆轴中,已知:圆轴直径d=100mm,轴向 拉力F=500kN,外力矩Me =7kN·m。求C点a =−30°截 面上的应力。 (b) C x x x x x y y y (a) x T F T C F