
称三倍标准误差椭圆为极限误差椭圆. 下表列出船位落入标准误差椭圆的概率。 表6-2误差椭圆概率表 c 力 c 0.1 0.0050 1.1 0.4539 2.1 0.8897 0.2 0.0198 1.2 0.5132 2.2 0.911 0.3 0.0440 1.3 0.5704 2.3 0.9290 0.4 0.0769 1.4 0.6247 2.4 0.9439 05 0.1175 1.5 0.6753 2.5 0.9561 0.6 0.1647 1.6 0.7220 2.6 0.9660 0.7 0.2173 1.7 0.7643 2.7 0.9739 0.8 0.2739 1.8 0.8021 2.8 0.9802 0.9 0.3330 19 0.8356 2.9 0.9851 1.0 0.3935 20 0.8647 3.0 0.9889 对应于两条船位线标准误差椭圆,其面积为:S-C si o 因为船位落入标准误差椭圆内的概率为定值(39.4%),所以标准误差椭圆的面积越小, 说明船位的精度越高。因此当观测两条船位线定位时,为了提高定位精度,除了提高船位线 精度外,还最好使两位置线交角接近90°。 用误差椭圆来评定船位精度,还能很好地反映船位散布的方向性.在短轴方向上,船位 分布范围最小,精度最高:长轴方向上,船位分布范围最广,精度最低。但是由于其作图复 杂,航海上不大采用. 在航海实践中,例如通过狭水道,应要求航线左右方向上船位分布尽量小,而在前后方 向上船位分布偏大些,对航行安全的影响相对小些。 6.3.3船位误差圆 以观测船位为圆心,以常数M为半径的圆称为船位误差圆 理论证明,任意多条独立观测船位线决定的最或是船位,它在任意两个垂直方向上的 标准误差的平方和的均方根设为常数M,即以最或是船位为原点O,建立任意的直角坐标 138
138 称三倍标准误差椭圆为极限误差椭圆. 下表列出船位落入标准误差椭圆的概率. 表 6-2 误差椭圆概率表 c P c c P c c P c 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 0.0050 0.0198 0.0440 0.0769 0.1175 0.1647 0.2173 0.2739 0.3330 0.3935 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 0.4539 0.5132 0.5704 0.6247 0.6753 0.7220 0.7643 0.8021 0.8356 0.8647 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 0.8897 0.9111 0.9290 0.9439 0.9561 0.9660 0.9739 0.9802 0.9851 0.9889 对应于两条船位线标准误差椭圆,其面积为: sin 1 2 S1 = 因为船位落入标准误差椭圆内的概率为定值( 0 39.4 0 ),所以标准误差椭圆的面积越小, 说明船位的精度越高. 因此当观测两条船位线定位时,为了提高定位精度,除了提高船位线 精度外,还最好使两位置线交角接近 0 90 . 用误差椭圆来评定船位精度,还能很好地反映船位散布的方向性. 在短轴方向上,船位 分布范围最小,精度最高;长轴方向上,船位分布范围最广,精度最低. 但是由于其作图复 杂,航海上不大采用. 在航海实践中,例如通过狭水道,应要求航线左右方向上船位分布尽量小,而在前后方 向上船位分布偏大些,对航行安全的影响相对小些. 6.3.3 船位误差圆 以观测船位为圆心,以常数 M 为半径的圆称为船位误差圆. 理论证明,任意多条独立观测船位线决定的最或是船位,它在任意两个垂直方向上的 标准误差的平方和的均方根设为常数 M ,即以最或是船位为原点 O ,建立任意的直角坐标

系XOY,XOY,则有: M=VG+o=V6+o,-=. (6.3.2) 特别有: M=√F+F (6.3.3) 其中a,b为标准误差椭圆的长、短半轴。 航海上称常数M为标准误差圆半径,而以观测船位为圆心,c·M为半径的圆称为c倍 标准误差圆。 1、标准误差圆半径 理论证明,n条(≥2)独立观测船位线所决定的最或是船位,其标准误差圆半径: M= ∑∑pp,sma,-ah向u, (6.3.4) 式中:[p)]表示船位线权总和: [P]表示船位线交点权总和:“表示单位权船位线标准误 差:P,表示第i条船位线权:C,表示第i 条船位线方位 (1)两条船位线时标准误差圆半径 如图6.3.4所示,由公式(6.3.4), 在两条船位线情况下,其标准误差圆半 径为: 图6.3.4 M= B+22 PiP:sin'()H ”B+P=u sino\ sino 即 M-回+a (6.3.5) sin 式中:,分别表示船位线、IⅡ的标准误差;0表示两条船位线的交角 特别地,当两条船位线等精度时,即0,=02=0,得: 139
139 系 XOY , X OY ,则有: 2 2 2 2 M x y x y = + = + = . (6.3.2) 特别有: 2 2 M a b = + . (6.3.3) 其中 a,b 为标准误差椭圆的长、短半轴. 航海上称常数 M 为标准误差圆半径,而以观测船位为圆心, c M 为半径的圆称为 c 倍 标准误差圆. 1、标准误差圆半径 理论证明, n 条 ( 2) n 独立观测船位线所决定的最或是船位,其标准误差圆半径: 1 2 [ ] sin ( ) [ ] n i i i j j i i j p p M p p P = = = − . (6.3.4) 式中: [ ] p 表示船位线权总和; [ ] P 表示船位线交点权总和; 表示单位权船位线标准误 差; i p 表示第 i 条船位线权; i 表示第 i 条船位线方位. (1)两条船位线时标准误差圆半径 如图 6.3.4 所示,由公式(6.3.4), 在两条船位线情况下,其标准误差圆半 径为: 1 2 2 1 2 2 1 sin ( ) p p M p p + = − 1 2 1 2 sin p p p p + = 1 2 1 1 sin p p = + 2 2 1 2 2 2 sin = + 2 2 1 2 sin + = . 即 2 2 1 2 sin M + = . (6.3.5) 式中: 1, 2 分别表示船位线 I、II 的标准误差; 表示两条船位线的交角. 特别地,当两条船位线等精度时,即 1 2 = = ,得: K1 1 2 F K3 X Y 图 6.3.4

M=a (6.3.6) sin@ (2)三条船位线时的标准误差圆半径 由公式(6.3.4),在三条船位线情况下,标准误差圆半径为: M= p+p2+p DP:sin(a-)+P:Psin(-a,)+p,psin(@-) 令:《=4-a,表示第1、Ⅱ两船位线的交角,B=%-a2表示第I、III两船位线的交 角,y=a一a表示第山、I两船位线的交角,则得 p+p:+p P sinssin 1 1 m口,mr,mE'“-m&,编,mg“ Pip:Pap pip P: P Vo:sin'y+aisin'B+o;sin'a 即 M= 0io;+003+oo (6.3.7) Vo:sin'y++osin'a M= (6.3.8) Vσsin'(a+β)+o2sin2B+osin'a 特别地,当三条船位线等精度时,设0=G=0,=0时,得: 3 M Vsiny+sinB+sina (6.3.9) 3 M (6.3.10) 2、船位落入误差圆的概率 设标准误差椭圆长半轴为a,短半轴为b,其比值k=。, 船位标准误差圆半径为 %
140 2 sin M = . (6.3.6) (2)三条船位线时的标准误差圆半径 由公式(6.3.4),在三条船位线情况下,标准误差圆半径为: 1 2 3 2 2 2 1 2 2 1 2 3 3 2 3 1 3 1 sin ( ) sin ( ) sin ( ) p p p M p p p p p p + + = − + − + − 令: = − 2 1 表示第 I、II 两船位线的交角, = − 3 2 表示第 II、III 两船位线的交 角, 3 1 = − 表示第 III、I 两船位线的交角,则得 1 2 3 2 2 2 1 2 2 3 3 1 sin sin sin p p p M p p p p p p + + = + + 1 2 2 3 3 1 2 2 2 3 2 1 1 1 1 sin sin sin p p p p p p p p p + + = + + 2 2 2 2 2 2 1 2 1 3 2 3 444 2 2 2 2 2 2 3 2 1 3 2 1 sin sin sin p p p + + = + + 2 2 2 2 2 2 1 2 1 3 2 3 2 2 2 2 2 2 2 1 3 sin sin sin + + = + + , 即 2 2 2 2 2 2 1 2 1 3 2 3 2 2 2 2 2 2 2 1 3 sin sin sin M + + = + + . (6.3.7) 或 2 2 2 2 2 2 1 2 1 3 2 3 2 2 2 2 2 2 2 1 3 sin ( ) sin sin M + + = + + + . (6.3.8) 特别地,当三条船位线等精度时,设 1 2 3 = = = 时,得: 2 2 2 3 sin sin sin M = + + . (6.3.9) 或 2 2 2 3 sin ( ) sin sin M = + + + . (6.3.10) 2、船位落入误差圆的概率 设标准误差椭圆长半轴为 a ,短半轴为 b ,其比值 b k a = ,船位标准误差圆半径为

M=√+6F.下面,只对k=0和k=1两种特殊情况讨论误差圆的概率问题 (1)k==0: 比时误装精圆是化为候老线段,商M=后+F=,今=a,超位落入误老 c-M内的概率等于(-ca,+ca)=(-co,+co)内的概率,所以当k=0时,船位落入: 一倍标准误差圆内的概率为:P1=68.3%: 二倍标准误差圆内的概率为:P。=95.3%: 三倍标准误差圆内的概率为:=99.7% (2)k==1, 此时误差椭圆变成圆形,而 M=Va2+b=√2a,c-M=√2ca. 因此,当k=1时,标准误差圆就是√互倍的标准误差椭圆,℃倍标准误差圆就是√2·c标 准误差椭圆,即:c倍标准误差圆内概率P。y等于√巨·c倍标准误差椭圆内的概率PE,而 Pre=1-e ifop =1-e2,所以 Bw=1-ee2」 (6.3.11) 于是当k=1时,船位落入: 倍标准误差圆内的概率为,=63.2% 二倍标准误差圆内的概率为P2=98.2%: 三倍标准误差圆内的概率为P,=99.99% 下表是在不同k值的情况下,一倍标淮误差园内的概率 表6-3一倍标准误差圆内的概率 k=6 0.0 0.1 0.3 0.5 0.7 0.9 1.0 a 68.3%68.2%67.7%66.3%66.1%63.3%63.2% 不同的c值下,船位落入误差圆内的概率是: c=1时,P=63.2%~68.3%
141 2 2 M a b = + . 下面,只对 k = 0 和 k =1 两种特殊情况讨论误差圆的概率问题. (1) 0 b k a = = : 此时误差椭圆退化为误差线段,而 2 2 2 2 2 (1 ) b M a b a a a = + = + = ,船位落入误差圆 c M 内的概率等于 (−ca , + ca) = (−c ,+ c ) 内的概率,所以当 k = 0 时,船位落入: 一倍标准误差圆内的概率为: 01 P = 68.3% ; 二倍标准误差圆内的概率为: 02 P = 95.3% ; 三倍标准误差圆内的概率为: 03 P = 99.7%. (2) 1 b k a = = : 此时误差椭圆变成圆形,而 M a b 2a 2 2 = + = ,cM = 2ca . 因此,当 k =1 时,标准误差圆就是 2 倍的标准误差椭圆, c 倍标准误差圆就是 2 c 标 准误差椭圆,即: c 倍标准误差圆内概率 PcM 等于 2 c 倍标准误差椭圆内的概率 2c P ,而 2 2 1 ( 2 ) 2 2 1 1 c c c P e e − − = − = − ,所以 2 1 c P e c M − = − . (6.3.11) 于是当 k =1 时,船位落入: 一倍标准误差圆内的概率为 11 P = 63.2% ; 二倍标准误差圆内的概率为 22 P = 98.2% ; 三倍标准误差圆内的概率为 33 P = 99.99% . 下表是在不同 k 值的情况下,一倍标准误差圆内的概率. 表 6-3 一倍标准误差圆内的概率 b k a = 0.0 0.1 0.3 0.5 0.7 0.9 1.0 P 68.3% 68.2% 67.7% 66.3% 66.1% 63.3% 63.2% 不同的 c 值下,船位落入误差圆内的概率是: c =1 时, 0 0 P = 63.2 ~ 0 0 68.3 ;
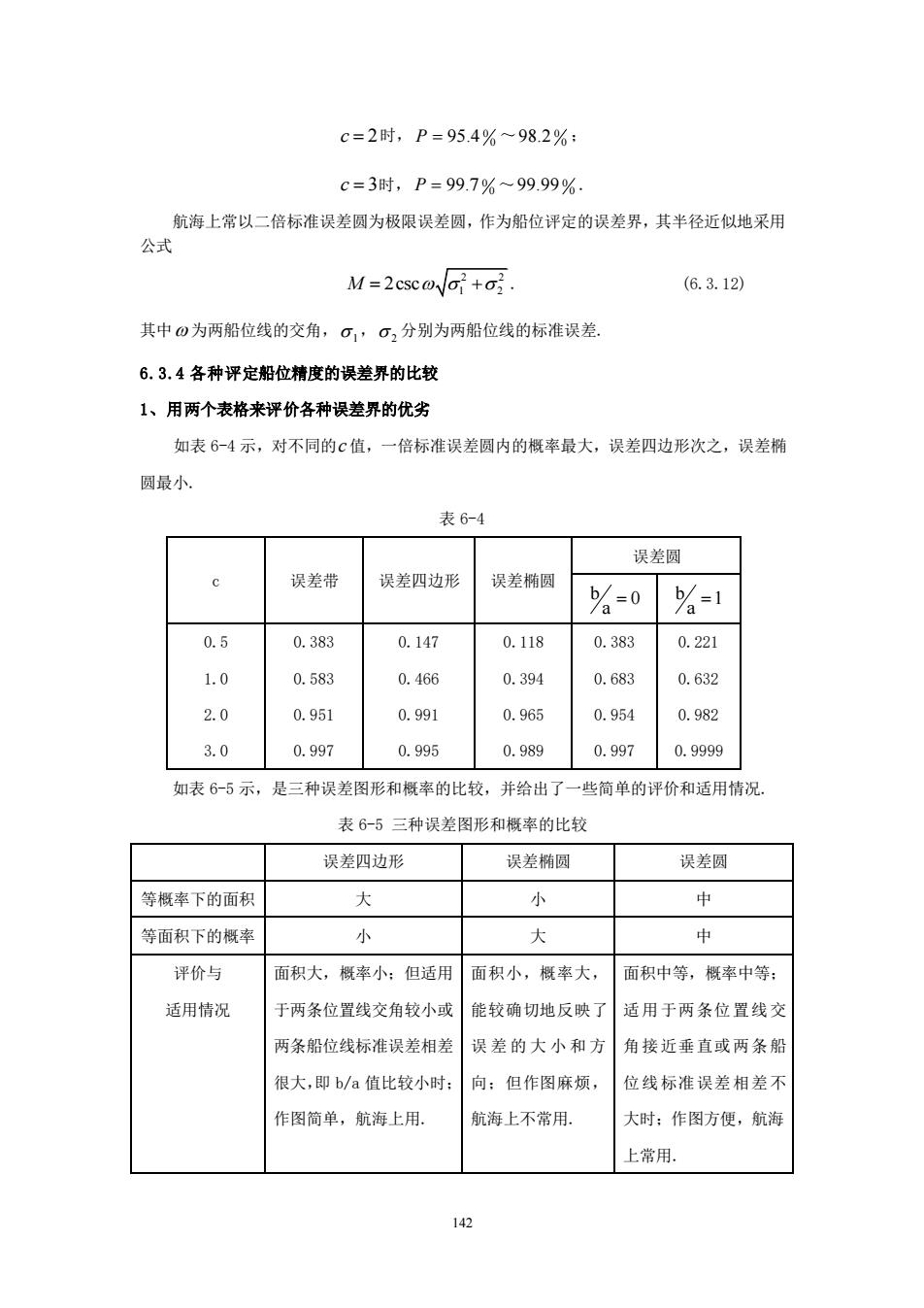
c=2时,P=95.4%~98.2%: c=3时,P=99.7%~99.99%. 航海上常以二倍标准误差圆为极限误差圆,作为船位评定的误差界,其半径近似地采用 公式 M=2csc@i+o (6.3.12 其中0为两船位线的交角,σ1,σ2分别为两船位线的标准误差 6.3.4各种评定船位精度的误差界的比较 1、用两个表格来评价各种误差界的优劣 如表6-4示,对不同的c值,一倍标准误差圆内的概率最大,误差四边形次之,误差椭 圆最小 表6-4 误差圆 c 误差带 误差四边形 误差椭圆 a-0 0.5 0.383 0.147 0.118 0.383 0.221 1.0 0.583 0.466 0.394 0.683 0.632 2.0 0.951 0.991 0.965 0.954 0.982 3.0 0.997 0.995 0.989 0.997 0.9999 如表6-5示,是三种误差图形和概率的比较,并给出了一些简单的评价和适用情况 表6-5三种误差图形和概率的比较 误差四边形 误差椭圆 误差圆 等概率下的面积 大 小 中 等面积下的概率 小 大 中 评价与 面积大,概率小:但适用面积小,概率大, 面积中等,概率中等: 适用情况 于两条位置线交角较小或能较确切地反映了 适用于两条位置线交 两条船位线标准误差相差 误差的大小和方 角接近垂直或两条船 很大,即b/a值比较小时: 向:但作图麻烦 位线标准误差相差不 作图简单,航海上用。 航海上不常用 大时:作图方便,航海 上常用
142 c = 2 时, 0 0 P = 95.4 ~ 0 0 98.2 ; c = 3 时, 0 0 P = 99.7 ~ 0 0 99.99 . 航海上常以二倍标准误差圆为极限误差圆,作为船位评定的误差界,其半径近似地采用 公式 2 2 1 2 M = + 2csc . (6.3.12) 其中 为两船位线的交角, 1, 2 分别为两船位线的标准误差. 6.3.4 各种评定船位精度的误差界的比较 1、用两个表格来评价各种误差界的优劣 如表 6-4 示,对不同的 c 值,一倍标准误差圆内的概率最大,误差四边形次之,误差椭 圆最小. 表 6-4 c 误差带 误差四边形 误差椭圆 误差圆 b 0 a = b 1 a = 0.5 1.0 2.0 3.0 0.383 0.583 0.951 0.997 0.147 0.466 0.991 0.995 0.118 0.394 0.965 0.989 0.383 0.683 0.954 0.997 0.221 0.632 0.982 0.9999 如表 6-5 示,是三种误差图形和概率的比较,并给出了一些简单的评价和适用情况. 表 6-5 三种误差图形和概率的比较 误差四边形 误差椭圆 误差圆 等概率下的面积 大 小 中 等面积下的概率 小 大 中 评价与 适用情况 面积大,概率小;但适用 于两条位置线交角较小或 两条船位线标准误差相差 很大,即 b/a 值比较小时; 作图简单,航海上用. 面积小,概率大, 能较确切地反映了 误差的大小和方 向;但作图麻烦, 航海上不常用. 面积中等,概率中等; 适用于两条位置线交 角接近垂直或两条船 位线标准误差相差不 大时;作图方便,航海 上常用