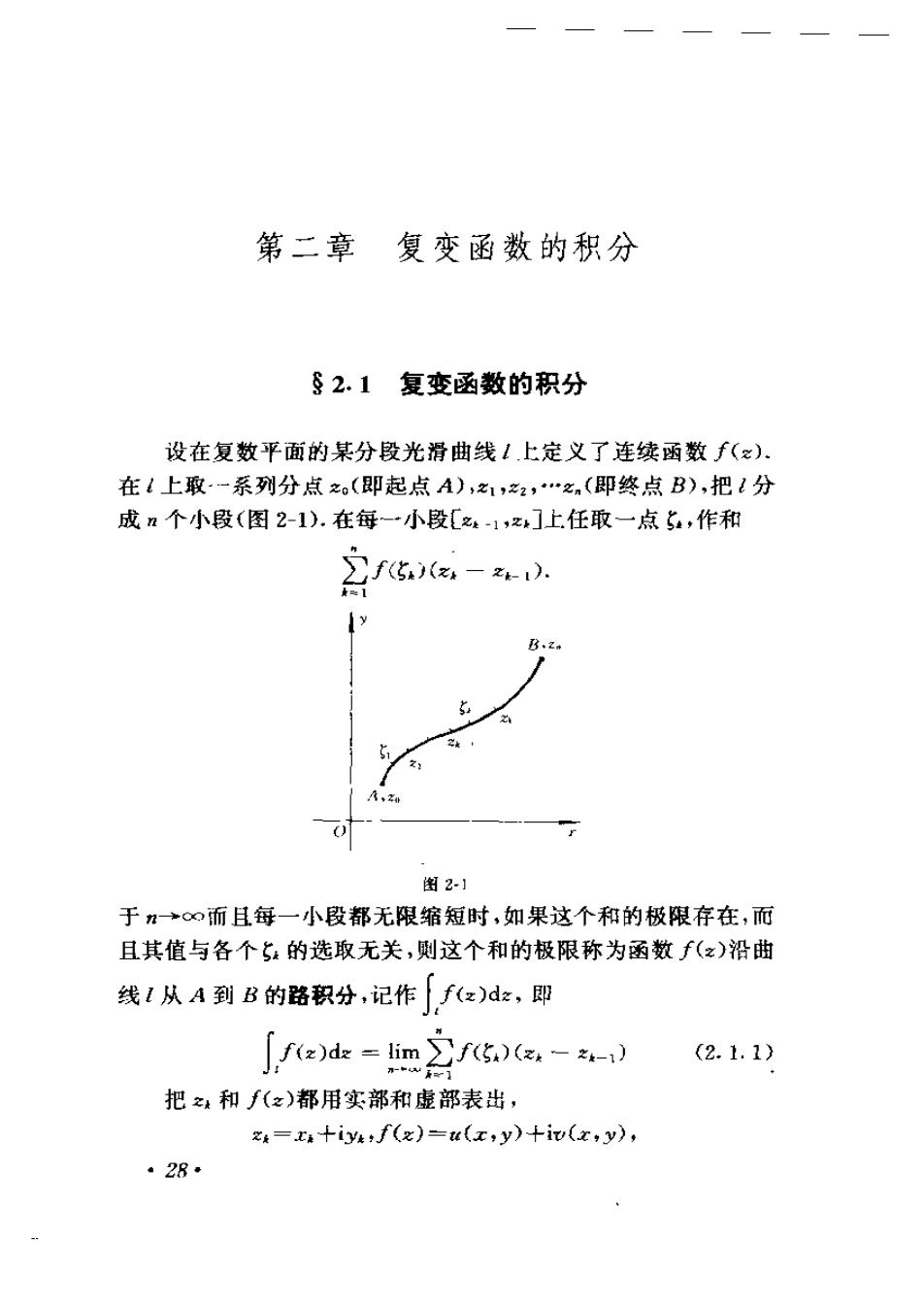
第二章复变函数的积分 §2.1复变函数的积分 设在复数平面的某分段光滑曲线1.上定义了连续函数f(). 在l上取一系列分点之(即起点A),之1,之2,“之n(即终点B),把l分 成n个小段(图2-1).在每-一小段[之-1z]上任取一点5,作和 2f-. y B.z 图2-1 于n∞而且每一小段都无限缩短时,如果这个和的极限存在,而 且其值与各个5:的选取无关,则这个和的极限称为函数f(z)沿曲 线1从A到B的路积分,记作」f(z)dz,即 「fe)de=lim2f5:)--) (2.1.1) n-re i] 把,和∫(之)都用实部和虚部表出, ze=x4十iytf(x)=w(x,y)十iv(x,y), ·28*

则ez=ax,y)dr-x,ydy +iv(x,y)dx+u(x,y)dy. (2.1.2) 这样,复变函数的路积分可以归结为两个实变函数线积分,它们分 别是路积分的实部和虚部.因面实变函数线积分的许多性质也对 路积分成立,例如 1.常数因子可以移到积分号之外, 2.函数的和的积分等于各个函数的积分之和, 3.反转积分路径,积分变号, 4.全路径上的积分等于各段上积分之和. 例试计算积分 1,-Rexds, Rezdz, 1、2分别如图2-2所示.两条路径的起点和终点相同,均自z=0 至之=1十i. 图2-2. 解先计算1, ,-dr+ay=之+i 再计算I2, ,=。idw+adr=合 ·29·

可见,两个积分,虽然被积函数相同,起点、终点亦相同,但由于积 分路径不同,其结果并不相同.一般说来,复变函数的积分值不仅 依赖于起点和终点,同时还与积分路径有关 §2.2柯西定理 §2.」指出,-~般说来,复变函数的积分值不仅依赖于积分的 起点和终点,而且与积分路径有关,本节就来时论复变函数的积分 值与积分路径的关系,主要介绍复变函数积分的重要定理一柯 定理.下面分两种情形来说明 (一)单通区域情形 所谓单通区城是这样的区域,在其中作任何简单的闭合围线, 围线内的点都是属于该区域内的点, 单通区域柯西定理如果函数f(x)在弹通区域上解析, 则沿B上任一分段光滑闭合曲线(也可以是B的边界),有 $,fe)dz=0. (2.2.1) 证明 按(2.1.2), 电fx)de=∮u(x,ydr-v(z,ydy +iydx+(ydy. 由于f:)在百上解析,因而器,在百上连续,对上式 右端实部虚部分别应用格林公式 .Pdx +Qdy- 2- drdy, (2.2.2) 将回路积分化成面积分,有 $reae=-j∬川器-影ddy+ij川器-8sddy. 同样,由于f(x)在B上解析,其实部和虚部在B上满足柯 ·30·

西-黎曼条件 au 00 3( x 33y ax ay 因而两个积分均为零,即得(2.2.1). 上述柯西定理还可以推广.如果函数f(z)在单通区域B上解 析,在闭单通区域多上连续,则沿B上任一分段光滑闭合曲线! (也可以是五的边界),有 ff(=0. 此定理的证明可参看例如,1.普里瓦洛夫的《复变函数引论》第 四章§2. (二)复通区域情形 有时,所研究的函数在区域上并非处处解析,而是在某些点或 者某些子区域上不可导(甚至不连续或根本没有定义),即存在奇 点,为了将这些奇点排除在区域之外,就需要作一些适当的闭合曲 线把这些奇点分隔出去,或者形象地说把这些奇点挖掉而形成某 种带“孔”的区域,即所谓复通区域 一般说来,在区域内,只要有一个简单的闭合曲线其内有不属 于该区域的点,这样的区域便称为复通区城. 对于区域(单通区域及复通区域)的境界线,通常这样来规定 其(内、外)正方向:当观察者沿着这个方向前进时,区域总是在观 察者的左边. 复通区域柯西定理 如果f(之)是闭复通区域上的单值解析 函数,则 (2.2.3) 式中!为区域外境界线,诸,为区域内境界线,积分均沿境界线的 正方向进行, 证明考虑图23中以l,1,2,…ln为境界的复通区域(图中 只画出,11,2),作割线连接内外境界线,原来的复通区域变成了 ·31

以ABL1BA',l的A''段,CDDC,l的CA段为境界线的单通 大域,而在这单通区域上(z)是解析的.按单通区域柯西定理 图2-3 ∮fe)dz+∫Afe)dx+$fe)de+」∫atfe)d t厂f(z)dz-+∮fede+∫ncfe)d+…=o. 其中沿同一割线两边缘上的积分值相互抵消,于是有 ∮,fe)z+∮fx)dz+$fzdk+…=0, 即得(2.2.3). 将(2.2.3)中求和项移到等号右边,改写成 $feda=-会$fed. 即 ∮fed&-∑∮,fed. (2.2.4) 这是说,沿内外境界线逆时针方向积分相等.[注意(2.2.4)积分号 上叠置的圆圈带有箭头!] 总结起来,柯西定理说的是 1.闭单通区域上的解析函数沿境界线积分为零, 2、闭复通区域上的解析函数沿所有内外境界线正方向积分 和为发、 ·32·