离散数学 正则图 Ks 3阶有向完全图 4阶竞赛图 定义11.8k-正则图一=&k的无向简单图 简单性质:knl2,当k是奇数时,n必为偶数. a 例Kn是(n-1)-正则图 彼得松图是3-正则图
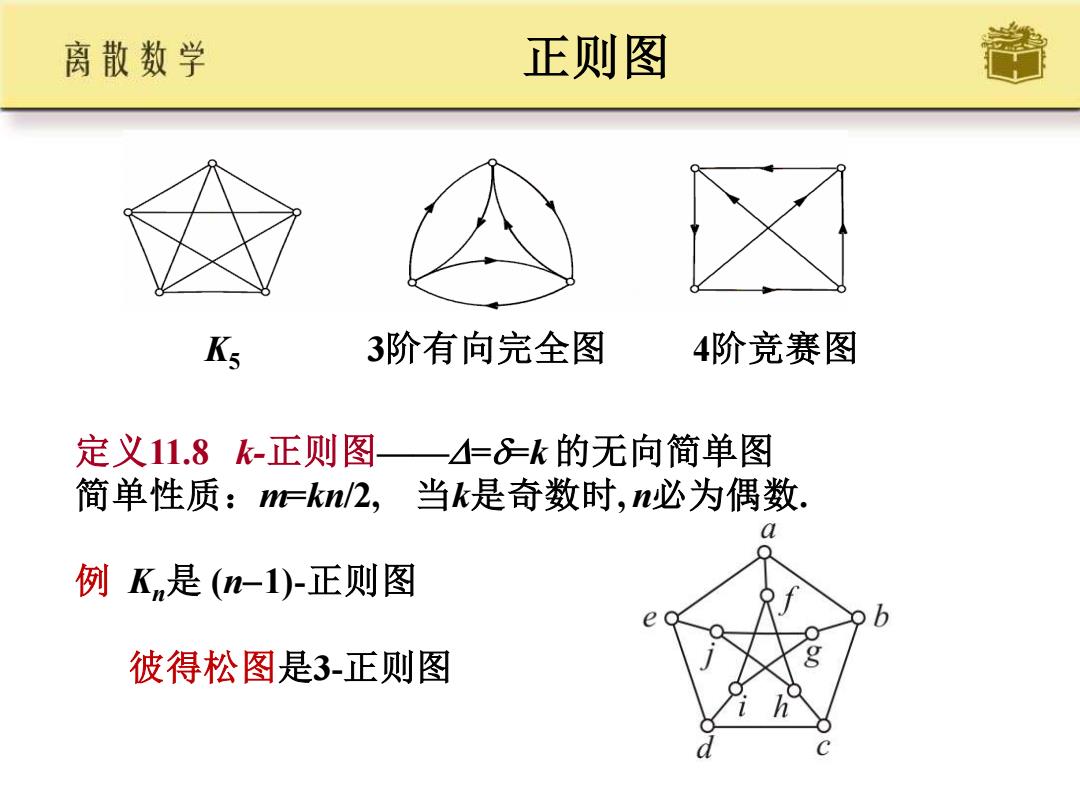
正则图 K5 3阶有向完全图 4阶竞赛图 定义11.8 k-正则图——==k 的无向简单图 简单性质:m=kn/2, 当k是奇数时, n必为偶数. 例 Kn是 (n−1)-正则图 彼得松图是3-正则图

离散数学 子图 定义11.9设两个图G=<V,E>,G'=<V,E>(同为无向图或 同为有向图),若V二V且E三E,则称G是G的子图,G为 G'母图,记作G'sG.又若V或EcE,则称G为G的真 子图.若G'∈G且V%V,则称G为G的生成子图. 设VcV且V≠O,称以Y为顶点集,以G中两个端点都在 V中的边组成边集的图为G中V的导出子图,记作GV).设 E1CE且E1≠O,称以E,为边集,以E,中边关联的顶点为顶点 集的图为G中E的导出子图,记作GE. 例 e, GHa,b,c GRen,e3]
子图 定义11.9 设两个图G=<V,E>, G =<V ,E >(同为无向图或 同为有向图), 若VV且EE,则称G是G的子图,G为 G 母图,记作G G. 又若VV或EE,则称G为G的真 子图. 若G G且V=V,则称G为G的生成子图. 设V1V且V1, 称以V1为顶点集, 以G中两个端点都在 V1中的边组成边集的图为G中V1的导出子图, 记作G[V1 ]. 设 E1E且E1, 称以E1为边集, 以E1中边关联的顶点为顶点 集的图为G中E1的导出子图, 记作G[E1 ]. 例 G G[{a,b,c}] G[{e1 ,e3 }]

离散数学 删除,收缩与加新边 定义11.10设G=<V,E>为无向图. (1)设eeE,用Ge表示从G中去掉边e,称为删除边e.又 设EcE,用G-E'表示从G中删除E中的所有边,称为删除 E'. (2)设v∈V,用G-表示从G中去掉v及所关联的所有边,称 为删除顶点v.又设V'cV,用G-V表示从G中删除V中所有 的顶点,称为删除V 3)设e=(u,)eE,用G\e表示从G中删除e后,将e的两个 端点u,v用一个新的顶点w(可以用u或v充当w)代替,并使w 关联除e以外w,关联的所有边,称为收缩边e. (4设u,veV(u,可能相邻,也可能不相邻),用GU(u,) (或G+(u,))表示在山,y之间加一条边(u,y),称为加新边 在收缩边和加新边过程中可能产生环和平行边. 18
18 定义11.10 设G=<V,E>为无向图. (1) 设eE,用G−e表示从G中去掉边e,称为删除边e.又 设EE,用G−E 表示从G中删除E中的所有边,称为删除 E. (2) 设vV,用G−v表示从G中去掉v及所关联的所有边,称 为删除顶点v.又设V V,用G−V 表示从G中删除V 中所有 的顶点,称为删除V. (3) 设e=(u,v)E,用G\e表示从G中删除e后,将e的两个 端点u,v用一个新的顶点w(可以用u或v充当w)代替,并使w 关联除e以外u,v关联的所有边,称为收缩边e . (4) 设u,vV(u,v可能相邻,也可能不相邻),用G(u,v) (或G+(u,v))表示在u,v之间加一条边(u,v),称为加新边. 在收缩边和加新边过程中可能产生环和平行边. 删除, 收缩与加新边
离散数学 实例 es e es e6 e V e6 e V2 v5 e6 e es e es 0 e3 V3 e V3 3 es G G-es G-{e1,e4 5 e6 e1 V2 e e6 e1 es es es e 3 V3 e3 e G-Vs G-{VsV5} G es 19
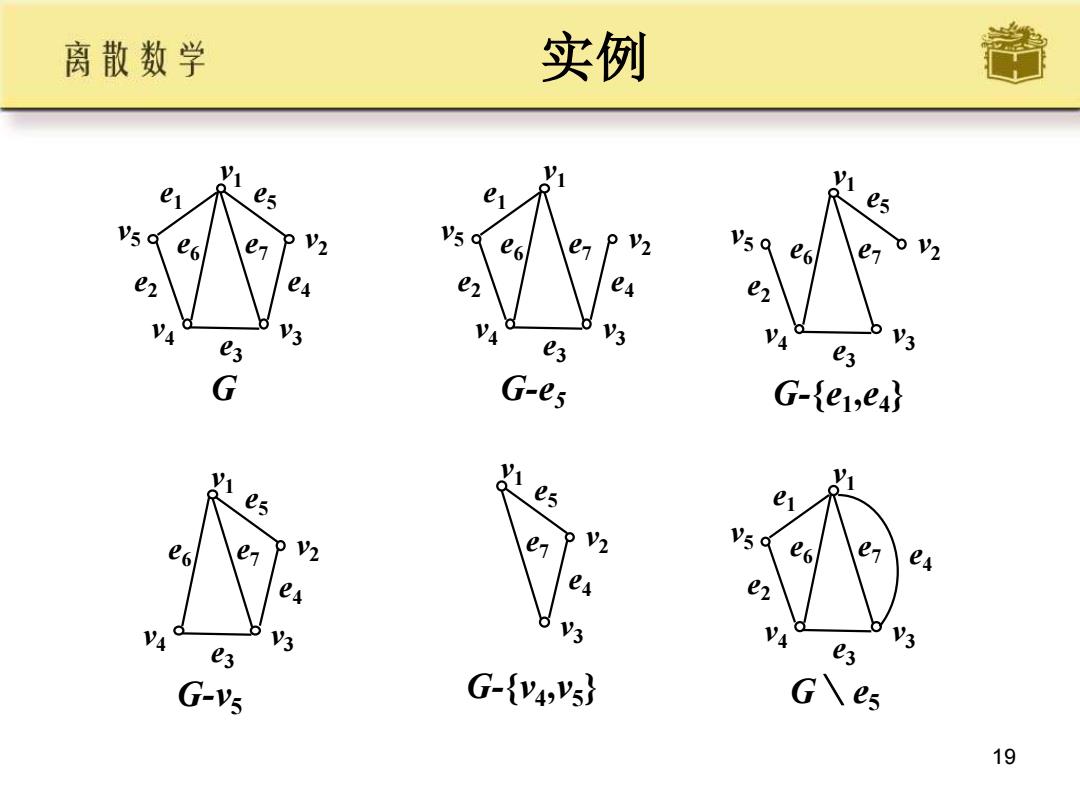
19 实例 v1 v2 v4 v3 v5 e1 e2 e3 e4 e5 e6 e7 G v1 v2 v4 v3 v5 e1 e2 e3 e4 e6 e7 G-e5 v1 v2 v4 v3 v5 e2 e3 e5 e6 e7 G-{e1 ,e4 } v1 v2 v4 v3 e3 e4 e5 e6 e7 G-v5 v1 v2 v3 e4 e5 e7 G-{v4 ,v5 } v1 v4 v3 v5 e1 e2 e3 e4 e6 e7 G\e5