离散数学 图的同构 定义11.5设G1=<V,E1>,G2=<V,E2>为两个无向图(两个有向 图),若存在双射函数fV→V,使得y∈1, (y)∈E,当且仅当()y》∈E2 (<,y吟∈E,当且仅当<ffy)>∈E2) 并且,(y(<旷)与()y》(fy>)的重数相 同,则称G与G2是同构的,记作GG2 例
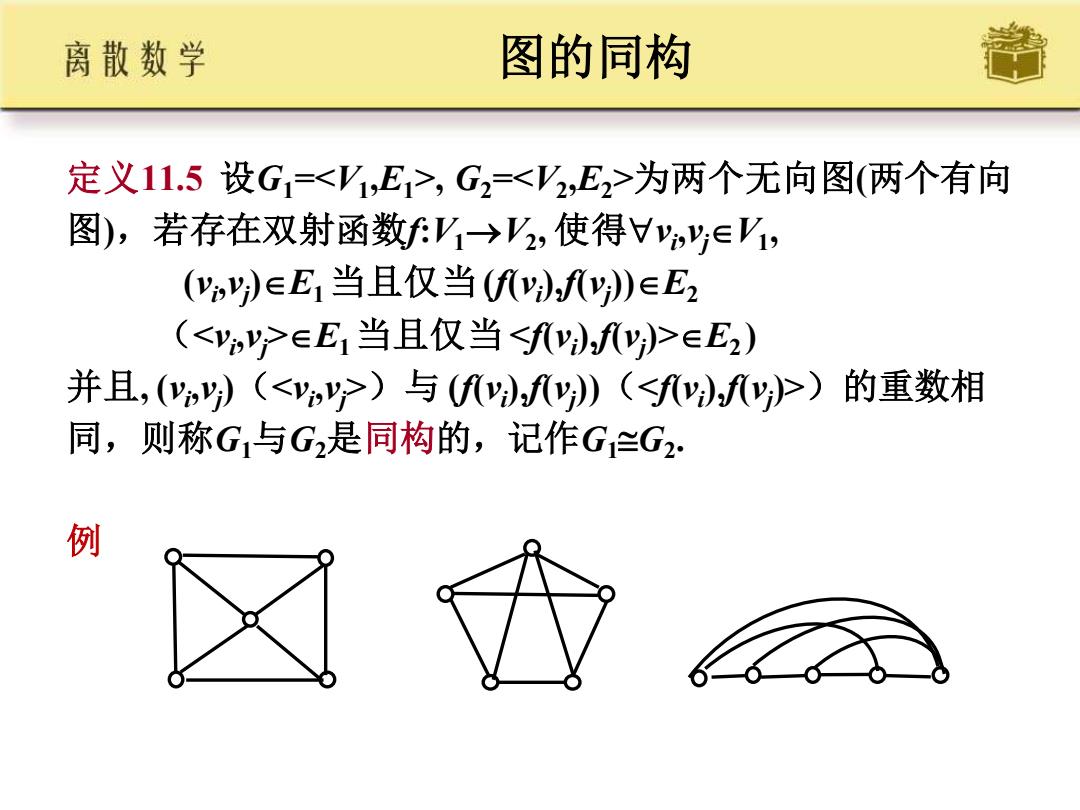
图的同构 定义11.5 设G1=<V1 ,E1>, G2=<V2 ,E2>为两个无向图(两个有向 图),若存在双射函数f:V1→V2 , 使得vi ,vjV1 , (vi ,vj )E1 当且仅当(f(vi ),f(vj ))E2 (<vi ,vj>E1 当且仅当 <f(vi ),f(vj )>E2 ) 并且, (vi ,vj )(<vi ,vj>)与 (f(vi ),f(vj ))(<f(vi ),f(vj )>)的重数相 同,则称G1与G2是同构的,记作G1G2 . 例
离散数学 图同构的实例 (1)与(2),(3)与(4),(⑤)与(6)均不同构. (1) (2) (3) (4) (5) (6) 说明:1.图的同构关系具有自反性、对称性和传递性. 2.判断两个图同构是个难题 12
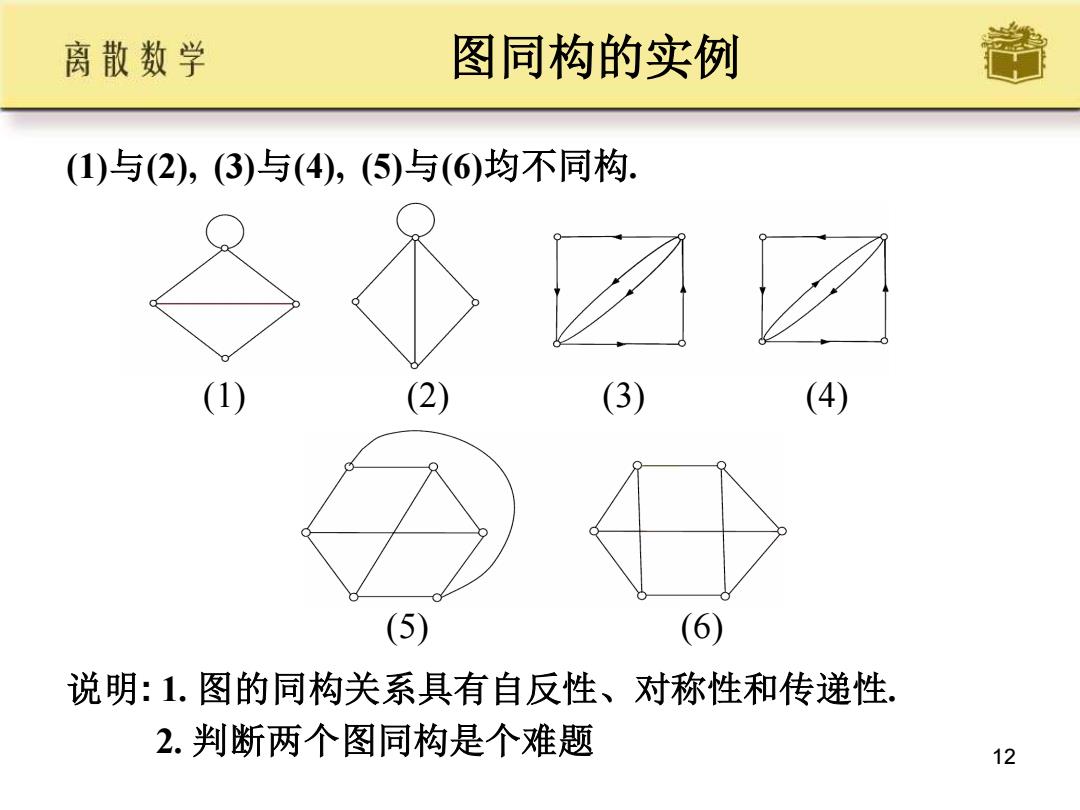
12 图同构的实例 (1) (2) (3) (4) (1)与(2), (3)与(4), (5)与(6)均不同构. (5) (6) 说明: 1. 图的同构关系具有自反性、对称性和传递性. 2. 判断两个图同构是个难题
离散数学 图同构的实例 所有4阶3条边非同构的简单无向图 (a) (b) (c) 所有3阶2条边非同构的简单有向图 (d) (e) () (g) 13
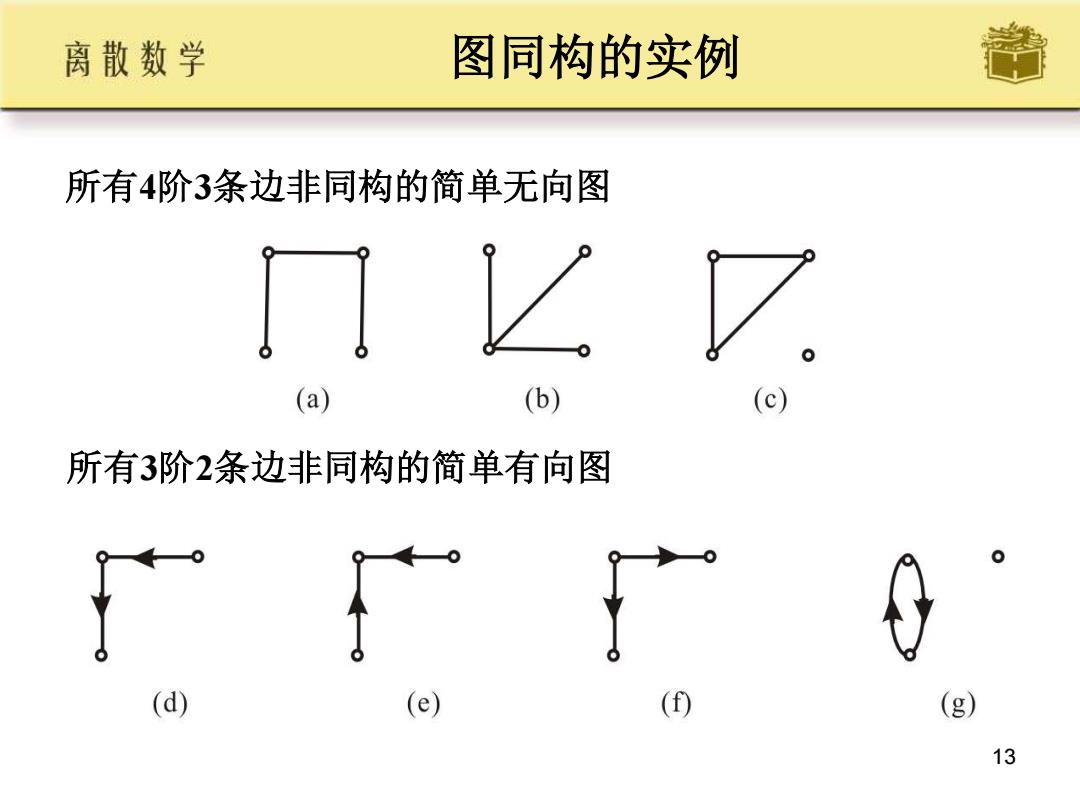
图同构的实例 所有4阶3条边非同构的简单无向图 13 所有3阶2条边非同构的简单有向图

离散数学 补图与自补图 定义11.6设G=<'V,E>为阶无向简单图,令 E={(u,)|u∈VAv∈VAu≠A(u,)EE, 称G=<V,E>为G的补图. 若G兰石则称G是自补图. 例 (a) (b) (c) (b)与(c)互为补图,(a是自补图
补图与自补图 定义11.6 设G=<V,E>为n阶无向简单图,令 ={(u,v) | uVvVuv(u,v)E}, 称 =<V, >为G的补图. 若G 则称G是自补图. E G E G 例 (b)与(c)互为补图,(a)是自补图.

离散数学 完全图与竞赛图 定义11.7 (1)n(21)阶无向完全图— 每个顶点与其余顶点均相邻的 无向简单图,记作Km 简单性质:n(n-1)/2,△=n-1 (2)n(21)阶有向完全图 每对顶点之间均有两条方向相 反的有向边的有向简单图. 简单性质:n(n-1),=2(n-1) t=8=小=8=n-1 (3)n(心1)阶竞赛图一基图为Kn的有向简单图. 简单性质:Fn(n-1)/2,△=n-1 15
15 完全图与竞赛图 定义11.7 (1) n (n1) 阶无向完全图——每个顶点与其余顶点均相邻的 无向简单图,记作Kn . 简单性质:m=n(n-1)/2, ==n-1 (2) n (n1)阶有向完全图——每对顶点之间均有两条方向相 反的有向边的有向简单图. 简单性质:m=n(n-1), ==2(n-1) += += −= −=n-1 (3) n (n1) 阶竞赛图——基图为Kn的有向简单图. 简单性质:m=n(n-1)/2, ==n-1