
幅相特性,即描述函数。为此要求非线性控制系统满足以下条件: 1.非线性元件N无惯性。 2.非线性元件N的特性是斜对称的,即f(e)=-f(-e)。因此在正弦信号作用 下,输出量的平均值等于零,没有恒定直流分量。前节所例举的典型非线性元件均 满足以上二个条件。 3.系统中的线性部份G(s)具有良好的低通滤波特性。这个条件对一般控制系 统来说是可以满足的,而且线性部份阶次越高,低通滤波特性越好。这一点使得非 线性元件输出量中的高次谐波通过线性部份后,其幅值被衰减的很小,近似认为只 有基波沿着闭环通道传递。显然这种近似的准确性完全取决于非线性元件输出信号 中高次谐波相对于基波成份的比例,高次谐波成份比例小,准确性高,反之,误差 较大。 8.2.2描球函数法的表示式 根据以上的基本思想和应用条件,可推导出非线性元件的数学模型一描述函数。 图&-7所示的非线性元件,假设它的输出量x()只与输入量(t)有关,即 x=f(e) 当输入量为正弦函数e()=Asin o1时,其输出x(t)一般是非正弦周期函数。 将输出x()用富氏级数展开,可以写成 ()(d cos Kor +B sin) (8-6) 考虑到非线性控制系统满足上述应用条件,则级数中的恒定分量A=O,高次谐 波可忽略。故式(8-6)可简化为 x(1)=A coso+B sin ax =Ci sindox+)(8-7) 式中 ',()(or) B ()sin ond(cox) C=42+B2 一基波分量的幅值 122
122 (8-6) 幅相特性,即描述函数。为此要求非线性控制系统满足以下条件: 1. 非线性元件 N 无惯性。 2. 非线性元件 N 的特性是斜对称的,即 f (e) = − f (−e) 。因此在正弦信号作用 下,输出量的平均值等于零,没有恒定直流分量。前节所例举的典型非线性元件均 满足以上二个条件。 3. 系统中的线性部份 G(s) 具有良好的低通滤波特性。这个条件对一般控制系 统来说是可以满足的,而且线性部份阶次越高,低通滤波特性越好。这一点使得非 线性元件输出量中的高次谐波通过线性部份后,其幅值被衰减的很小,近似认为只 有基波沿着闭环通道传递。显然这种近似的准确性完全取决于非线性元件输出信号 中高次谐波相对于基波成份的比例,高次谐波成份比例小,准确性高,反之,误差 较大。 8.2.2 描述函数法的表示式 根据以上的基本思想和应用条件,可推导出非线性元件的数学模型—描述函数。 图 8-7 所示的非线性元件,假设它的输出量 x(t) 只与输入量 e(t) 有关,即 x = f (e) 当输入量为正弦函数 e(t) = Asin t 时,其输出 x(t) 一般是非正弦周期函数。 将输出 x(t) 用富氏级数展开,可以写成 = = + + 0 0 ( ) ( cos sin ) k K k x t A A Kt B Kt 考虑到非线性控制系统满足上述应用条件,则级数中的恒定分量 A0=0,高次谐 波可忽略。故式(8-6)可简化为 ( ) cos sin sin( ) = 1 + 1 = 1 +1 x t A t B t C t 式中 ( ) cos ( ) 1 2 0 1 2 A x t td t = ( )sin ( ) 1 2 0 1 2 B x t td t = 2 1 2 C1 = A1 + B -基波分量的幅值 (8-7)
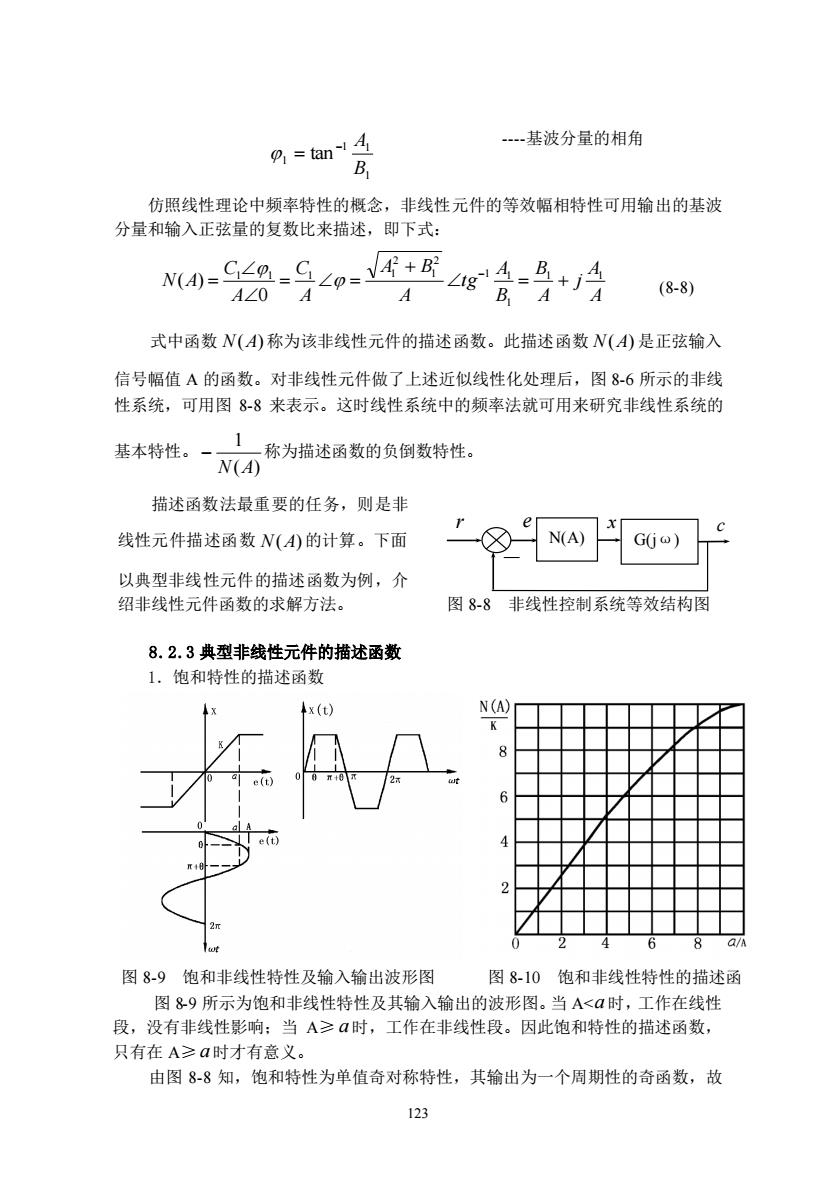
9=tan 基波分量的相角 B 仿照线性理论中频率特性的概念,非线性元件的等效幅相特性可用输出的基波 分量和输入正弦量的复数比来描述,即下式: N0=Sg-S∠0=V霄+R A∠0A A B A (8-8) 式中函数N(A)称为该非线性元件的描述函数。此描述函数N(A)是正弦输入 信号幅值A的函数。对非线性元件做了上述近似线性化处理后,图86所示的非线 性系统,可用图88来表示。这时线性系统中的颜率法就可用来研究非线性系统的 1 基本特性。 称为描述函数的负倒数特性。 N(A) 描述函数法最重要的任务,则是非 线性元件描述函数N(4)的计算。下面 e N(A) G() 以典型非线性元件的描述函数为例,介 绍非线性元件函数的求解方法。 图8-8非线性控制系统等效结构图 8.2.3典型非线性元件的描述函数 1.,饱和特性的描述函数 x(t) (A 图89饱和非线性特性及输入输出波形图 图8-10饱和非线性特性的描述函 图&9所示为饱和非线性特性及其输入输出的波形图。当A<a时,工作在线性 段,没有非线性影响:当A≥☑时,工作在非线性段。因此饱和特性的描述函数, 只有在A≥a时才有意义。 由图8-8知,饱和特性为单值奇对称特性,其输出为一个周期性的奇函数,故
123 (8-8) 1 1 1 1 tan B − A = 仿照线性理论中频率特性的概念,非线性元件的等效幅相特性可用输出的基波 分量和输入正弦量的复数比来描述,即下式: A A j A B B A t g A A B A C A C N A 1 1 1 1 1 2 1 2 1 1 1 1 0 ( ) = + + = = = − 式中函数 N(A) 称为该非线性元件的描述函数。此描述函数 N(A) 是正弦输入 信号幅值 A 的函数。对非线性元件做了上述近似线性化处理后,图 8-6 所示的非线 性系统,可用图 8-8 来表示。这时线性系统中的频率法就可用来研究非线性系统的 基本特性。 ( ) 1 N A − 称为描述函数的负倒数特性。 描述函数法最重要的任务,则是非 线性元件描述函数 N(A) 的计算。下面 以典型非线性元件的描述函数为例,介 绍非线性元件函数的求解方法。 图 8-8 非线性控制系统等效结构图 8.2.3 典型非线性元件的描述函数 1.饱和特性的描述函数 图 8-9 饱和非线性特性及输入输出波形图 图 8-10 饱和非线性特性的描述函 图 8-9 所示为饱和非线性特性及其输入输出的波形图。当 A< a 时,工作在线性 段,没有非线性影响;当 A≥ a 时,工作在非线性段。因此饱和特性的描述函数, 只有在 A≥ a 时才有意义。 由图 8-8 知,饱和特性为单值奇对称特性,其输出为一个周期性的奇函数,故 e x c — — N(A) G(jω) -基波分量的相角 r