
11.2二维金属目标的散射 1956 2)当x,和x,m重合时,利用Hankel函数的小宗量近似(r→oo) (a)1-2n巡 2 2 y=1.781 二mm中的积分可以写成 11- x=△x/2 -引u(】 7
7 11.2 二维金属目标的散射 2)当xn和xm重合时,利用Hankel函数的小宗量近似(r→∞) ( ) ( ) 2 0 2 1 j ln 2 kx H kx − γ = 1.781 zmn中的积分可以写成 0 2 ' 1 j ln d ' 2 2 j ln ln 2e x k x x I x x x x x x k x x x − = − − = − + − x x = 2 2 1 j ln 4e mm k x z x = −
11.2二维金属目标的散射 966 3)处理相邻的小段时,直接计算也会产生奇异性,对矩阵元素的精度有较大 的影响。因此,对于m-n=1的情况,采用和计算zmm相同的方法,有 m Ar-jAx 2 Toeplitz矩阵 4 例金属薄条带宽度L=3,其上划分300个网格。 20 12 15 p∈[0°,90°] p=90° 10 10 8 0. 6 .10 0.0 0.5 1.01.52.02.53.0 0 20 40 6080100120140160180 位置(波长) Phi() 8
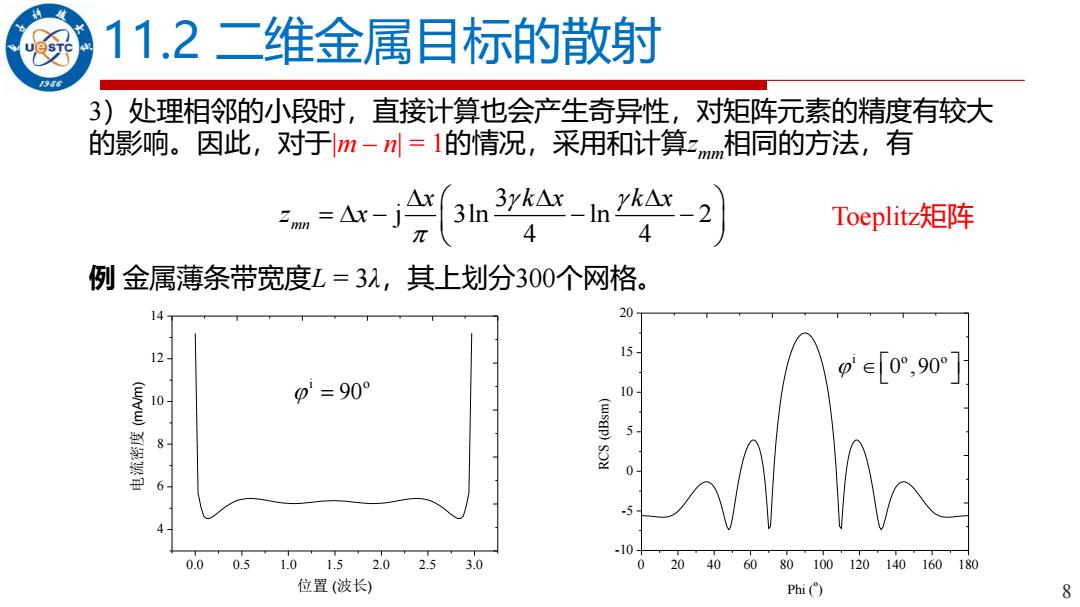
8 11.2 二维金属目标的散射 3)处理相邻的小段时,直接计算也会产生奇异性,对矩阵元素的精度有较大 的影响。因此,对于|m – n| = 1的情况,采用和计算zmm相同的方法,有 3 j 3ln ln 2 4 4 mn x k x k x z x = − − − Toeplitz矩阵 例 金属薄条带宽度L = 3λ,其上划分300个网格。 0.0 0.5 1.0 1.5 2.0 2.5 3.0 4 6 8 10 12 14 电流密度 (mA/m) 位置 (波长) i o = 90 0 20 40 60 80 100 120 140 160 180 -10 -5 0 5 10 15 20 RCS (dBsm) Phi (o) i o o 0 ,90

11.2二维金属目标的散射 966 二分域三角基函数和Galerkin法 由上图可知,感应电流在条带两端不为零。因此可将条带分为N-1段,每一段长 度△x=L/(N-1),共有N个三角基函数,其中完整三角N-2个、半三角2个 XXX /XX XI X2 X3 XN-2 XN-1 XN 1)当源点和场点不重合且不相邻时(m-n>1) ()f()x)dx'd 采用M点的高斯求积公式展开上式 求积节点 求积系数 之∑(,)(,)H(。-x) 9
9 11.2 二维金属目标的散射 二 分域三角基函数和Galerkin法 由上图可知,感应电流在条带两端不为零。因此可将条带分为N-1段,每一段长 度 = − x L N( 1) ,共有N个三角基函数,其中完整三角N-2个、半三角2个 1)当源点和场点不重合且不相邻时(|m – n| > 1) ( ) ( ) ( ) ( ) 2 0 ' ' d 'd m n mn m n f f z f x f x H k x x x x = − x3 x1 x2 …… xN xN-1 xN-2 采用M点的高斯求积公式展开上式 ( ) ( ) ( ) ( ) ( ) ( ) 2 0 1 1 M M mn m p m p n q n q p q p q z w x f x w x f x H k x x = = = − 求积节点 求积系数

11.2二维金属目标的散射 956 数值求积公式:∫心fx)=∑AfK)+RLfI k=0/ 求积系数 求积节点 梯形公式: [fes22a+fo= 代数精度:1 梯形公式 辛普森公式: rx≈。2fo)+4f1+f1=s 代数精度:3 高斯公式:指定求积节点,构造出更高精度的求积公式 代数精度:2n-1 复化求积公式:将求积区间分成若干小区间,应用低阶求积公式,再求和 10
10 11.2 二维金属目标的散射 ( ) ( ) [ ] 0 f x dx A f x R f n k k k b a = + = 数值求积公式: ( ) [ ( ) ( )] ( ) a b 2 b a b a f x dx f a f b T f − + = 梯形公式: 辛普森公式: ( ) [ ( ) 4 ( ) ( )] ( ) 6 2 b a b a a b f x dx f a f f b S f − + + + = 梯形公式 高斯公式:指定求积节点,构造出更高精度的求积公式 代数精度:1 代数精度:3 代数精度:2n-1 求积系数 求积节点 复化求积公式:将求积区间分成若干小区间,应用低阶求积公式,再求和