
三、小结 二阶和三阶行列式是由解二元和三元线性方 程组引入的. 二阶与三阶行列式的计算—一对角线等法则 012 =41122-012421 21 22 11 an 13 1 22 023 =41122033+1202331+4132132 a3 32 33 -4112332-%12421433-132231, 上页 返回
二阶和三阶行列式是由解二元和三元线性方 程组引入的. 二阶与三阶行列式的计算 对角线等法则 . 11 22 12 21 21 22 11 12 a a a a a a a a = − 1 1 2 3 3 2 1 2 2 1 3 3 1 3 2 2 3 1, 1 1 2 2 3 3 1 2 2 3 3 1 1 3 2 1 3 2 a a a a a a a a a a a a a a a a a a − − − = + + 31 32 33 21 22 23 11 12 13 a a a a a a a a a 三、小结

思考题 W L12 13 14 称四阶方阵A= 21 L22 M23 l24 对应的表达式 a31 L32 33 34 41 42 L43 044 11 12 13 L14 A 01 L22 23 L24 a31 432 L33 34 L41 L42 L43 L44 为四阶行列式,请问:四阶行列式展开后共有 多少个乘积项,能不粳用类似沙路法则? 上页 返回
思考题 称四阶方阵 对应的 = 4 1 4 2 4 3 4 4 3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 a a a a a a a a a a a a a a a a A 41 42 43 44 31 32 33 34 21 22 23 24 11 12 13 14 a a a a a a a a a a a a a a a a A = 表达式 多少个乘积项,能不能使用类似沙路法则? 为四阶行列式,请问:四阶行列式展开后共有

思考题解答 解 共有4!=24个乘积项;不能用所的沙路法则 上页 返回
思考题解答 解 共有4!= 24个乘积项;不能用所谓的沙路法则!

第二章行列式 第二节n阶行列式 一、余子式和代数余子式 > 二、行列式按行(列)的展开法则 三、小节、思考题
第二章 行列式 第二节 n 阶行列式 一、余子式和代数余子式 二、行列式按行(列)的展开法则 三、小节、思考题
n阶行列式的定义 11 412 定义对任意n阶方阵A= 21 22 用记号 Qn2 11 412 n A= 21 L22 表示一个与矩阵A相联系 An2 的数或表达式,常称A为A的行列式或记为detA) 上页 返回
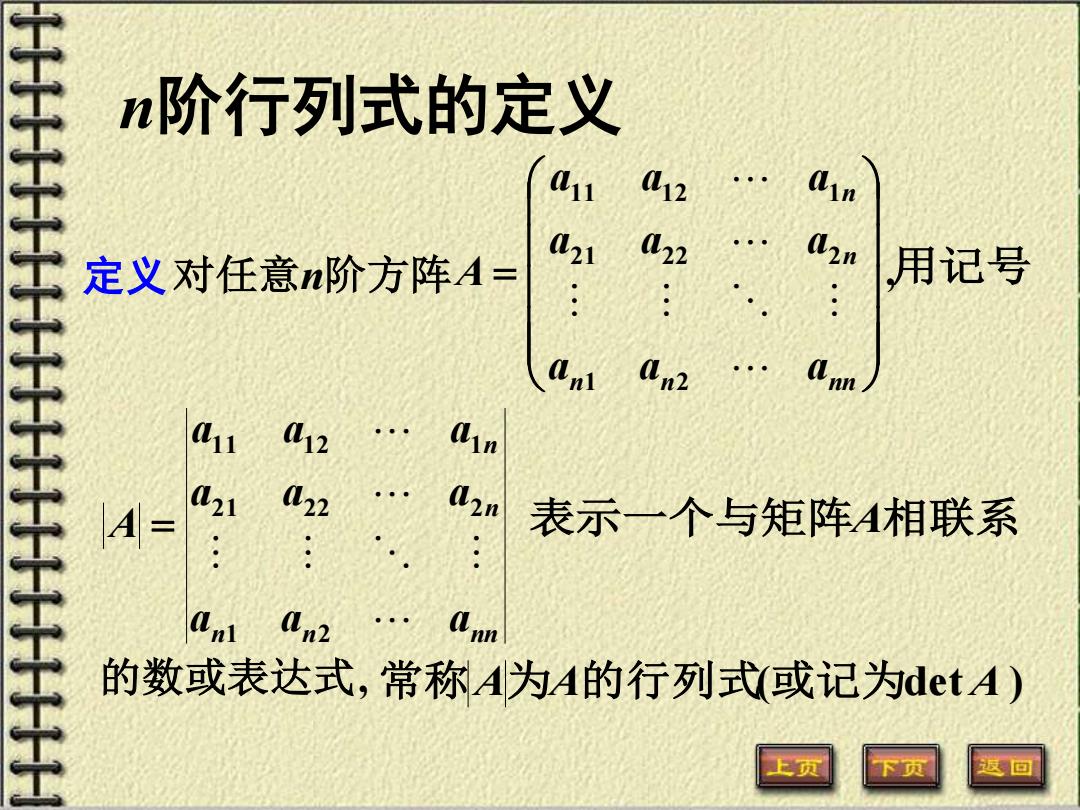
n阶行列式的定义 定义 对任意n阶方阵 , 1 2 21 22 2 11 12 1 = n n nn n n a a a a a a a a a A 用记号 n n nn n n a a a a a a a a a A 1 2 21 22 2 11 12 1 = 表示一个与矩阵A相联系 的数或表达式, 常称A为A的行列式(或记为det A )