
3.3支路电流法 1.支路电流法→以各支路电流为未知量列写 电路方程分析电路的方法。 对于有个结点、b条支路的电路,要求解支路 电流,未知量共有b个。只要列出b个独立的电路方 程,便可以求解这b个变量。 2.独立方程的列写 ①从电路的n个结,点中任意选择n-l个结,点列写 KCL方程 ②选择基本回路列写b-(-1)个KVL方程
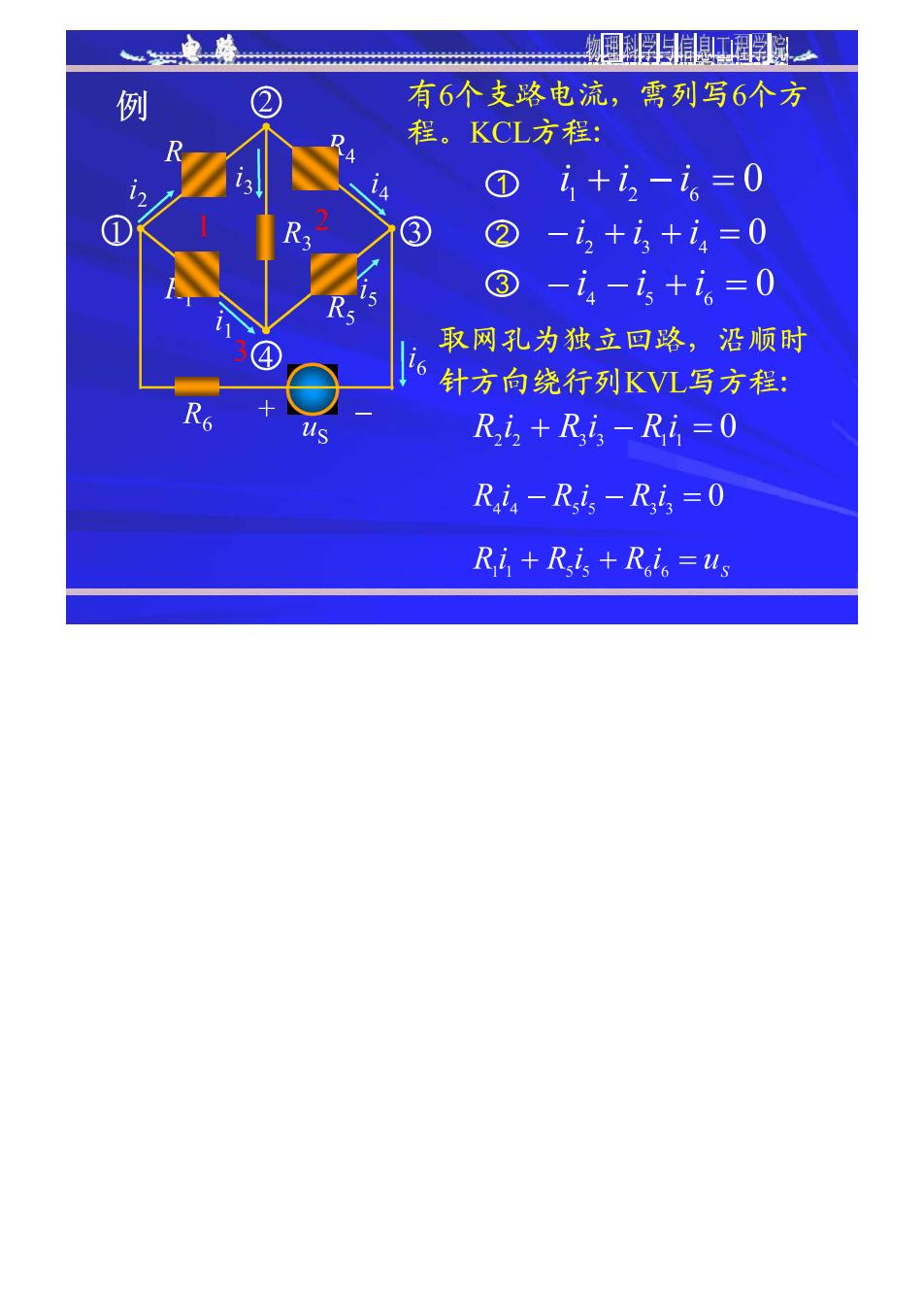
例 有6个支路电流,霄列写6个方 程。KCL方程: ① 2+i2-。=0 2 ② -i2ti3+i4=0 -i-i+i。=0 取网孔为独立回路,沿顺时 针方向绕行列KVL写方程: R2+,-Ri=0 Ris-Ris-Ris=0 Ri+Ri+Ri。=us

乡小结 (1)支路电流法的一般步聚: ①标定各支路电流的参考方向; ②选定(1)个结点,列写其KCL方程; ③选定b(-1)个独立回路,指定回路绕行方 向,结合KVL和支路方程列写; ∑Ri=∑4x 当i,的参考方向与回路的方向一致时R取正号,反 之取负号;当电源电压山与回路方向一致时取负号,反 之取正号;电源电压包括电压源的激励电压和电流源引起 的电压(有并联电阻的电流源可以使用等效电压源,否则 可以把电流源电压作为变量)。 ④求解方程,得到支路电流;然后计算电压和进行其 它分析

(2)支路电流法的特点: 支路法列写的是KC和KVL方程,所以方程 列写方便、直观,但方程数较多,宜于在支路数不 多的情况下使用。 例1求冬支路电流及各电压源发出的功率。 a 解 ①n-1=1个KCL方程: 7Ω 结点a:-1-12+3=0 7Ω ②b(n-1)-2个KVL方程: 70 711-1112=70-6=64 1112+713=6 利用克莱姆法则求解线性方程组

国臭 41西十a2+…+41wx=乌, am+an3+…+a不=b, aw1西+aw2五+…Gm不=b (1.22) 其解可以用公式给出,即有 克菜姆(Cramer)法则如果线性方程组(1.22)的系数行列式不等于零,即 克莱姆法则 1 ap Giw D= 22 … ≠0, 口u a 则方程组(1.22)有唯一解 (j=1,2…,8), (1.23) 其中D,是把系数行列式D中第列的元素用方程组右端的常数代替后所得到的”阶行列式,即 an … 4-14 41+1 s Di= 21 a2j 5 n … a-1 41 d