
液柱处于静止时,上述三项力的合力为零:P2 A- P,A- pgA(zi - z2) = 0压力形式p, = p, + pg(z, -z, + z2g+ z1g能量形式O静力学基本方程
液柱处于静止时,上述三项力的合力为零: 0)( − 12 − ρ − zzgAApAp 21 = )( 12 21 = + ρ − zzgpp gz p gz p 2 2 1 1 +=+ ρ ρ ——静力学基本方程 压力形式 能量形式

讨论:(1)适用于重力场中静止、连续的同种不可压缩性流体;(2)物理意义:zg单位质量流体所具有的位能,J/kg;p单位质量流体所具有的静压能,J/kg。p在同一静止流体中,处在不同位置流体的位能和静压能各不相同,但二者可以转换,其总和保特不变
讨论: (1)适用于重力场中静止、连续的同种不可压缩性 流体; (2)物理意义: zg ——单位质量流体所具有的位能,J/kg; ρ p ——单位质量流体所具有的静压能,J/kg。 在同一静止流体中,处在不同位置流体的位能和静 压能各不相同,但二者可以转换,其总和保持不变

(3)在静止的、连续的同种流体内,处于同一水平面上各点的压力处处相等。压力相等的面称为等压面。(4)压强具有传递性:液面上方压强变化时,液体内部各点的压强也将发生相应的变化。(5)压强的大小可用一定高度的液体柱来表示。pi- P2 = hpg当用液柱高度来表示压强或压强差时,必须注明是何种液体,否则就失去意义
(3)在静止的、连续的同种流体内,处于同一水平面上 各点的压力处处相等。压力相等的面称为等压面。 (4)压强具有传递性:液面上方压强变化时,液体内部 各点的压强也将发生相应的变化。 (5)压强的大小可用一定高度的液体柱来表示。 h g pp = − ρ 21 当用液柱高度来表示压强或压强 差时,必须注明是何种液体,否 则就失去意义
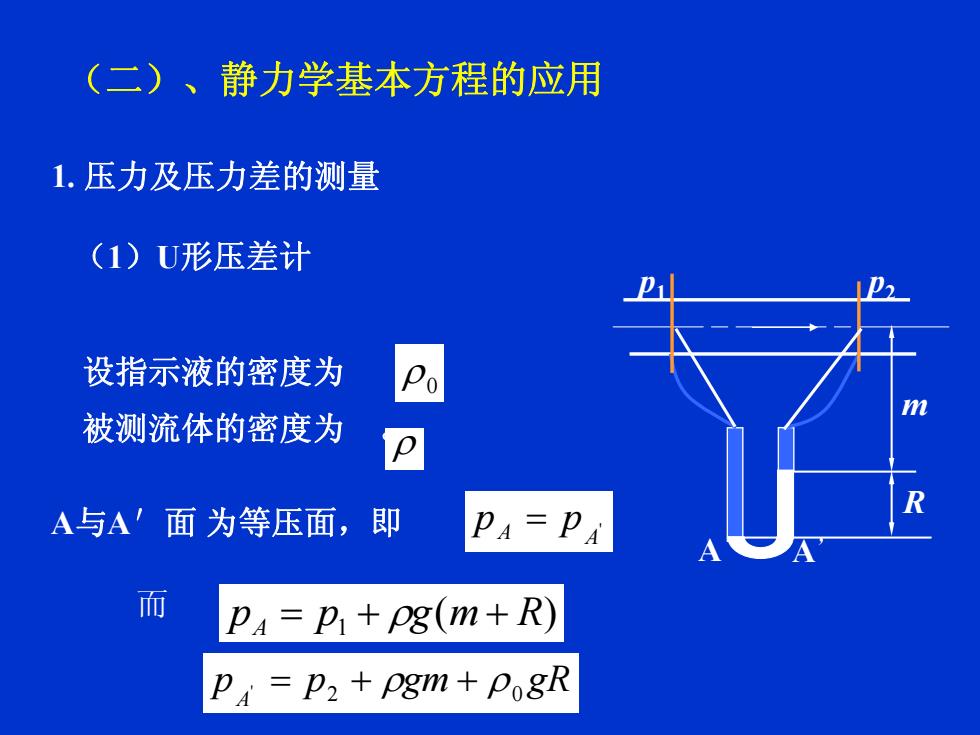
(二)、静力学基本方程的应用1.压力及压力差的测量(1)U形压差计设指示液的密度为m被测流体的密度为pRA与A面为等压面,即PA=PA而P= pi + pg(m+R)PA=P2+pgm+PogR
(二)、静力学基本方程的应用 1. 压力及压力差的测量 ( 1 ) U形压差计 设指示液的密度为 , 被测流体的密度为 。 ρ ρ 0 A 与 A′面 为等压面,即 ' A A = pp )( 1 RmgppA = + ρ + gRgmpp A' = 2 + ρ + ρ 0 而 p 1 p 2 m R A A’

所以Pi + pg(m + R)= P2 + pgm + PogRPi - P2 =(Po - p)gR整理得若被测流体是气体,则有p<<poPi- P2 ~ Rgpo(2)指示液的选取:指示液与被测流体不互溶,不发生化学反应;C其密度要大于被测流体密度。应根据被测流体的种类及压差的大小选择指示液
所以 gRgmpRmgp1 2 0 + ρ + )( = + ρ + ρ 整理得 − pp = ρ 021 − ρ)( gR 若被测流体是气体, ,则有 ρ << ρ 0 − 21 ≈ Rgpp ρ 0 (2)指示液的选取: 指示液与被测流体不互溶,不发生化学反应; 其密度要大于被测流体密度。 应根据被测流体的种类及压差的大小选择指示液