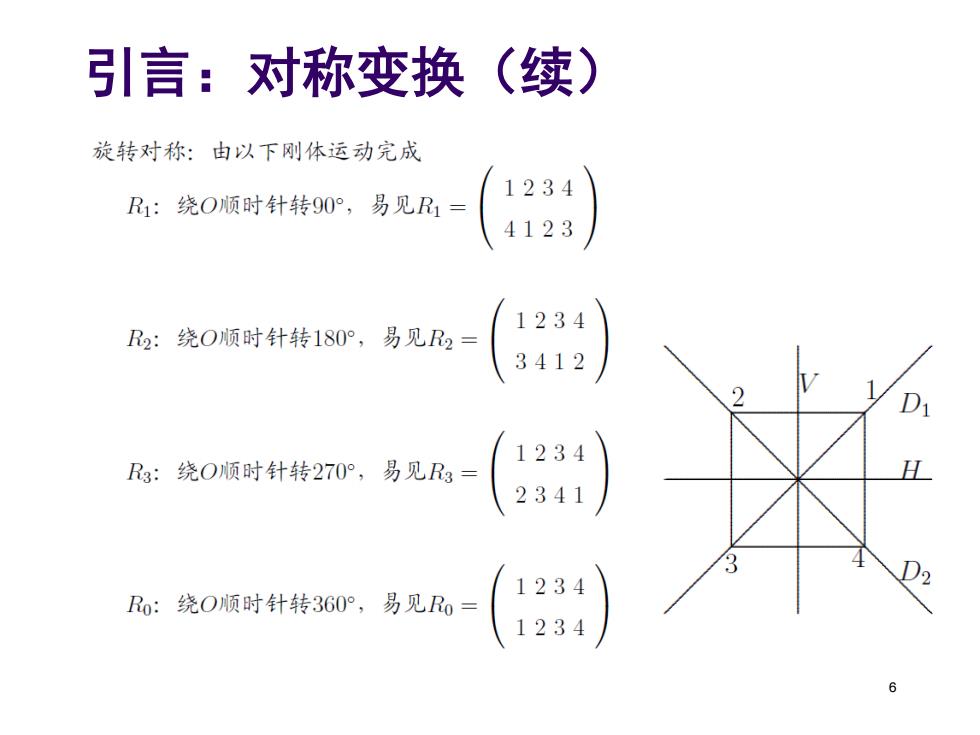
引言:对称变换(续) 旋转对称:由以下刚体运动完成 R1:绕O顺时针转90°,易见B1= 1234 4123 2:绕O顺时针转180°,易见B2= 1234 3412 Rg:绕O顺时针转270°,易见R3= 1234 2341 1234 R:绕O顺时针转360°,易见R0= 1234
引言:对称变换(续) 6

引言:对称变换(续) 反射对称:由以下刚体运动完成 H:对于水平中线H的反射。D1:对于对角线D1的反射。 V:对于垂直中线V的反射。D2:对于对角线D2的反射。 a()r()a-(a)(d
引言:对称变换(续) 7

引言:对称变换(续) ·两个对称变换的连续作用依然是对称变换 例如:R1*H指先右转90°,后 做水平反射,结果得D1,故 R1*H=D1;而H*R1=D2: 由此可以看出R1*H≠H*R1
引言:对称变换(续) 8 两个对称变换的连续作用依然是对称变换
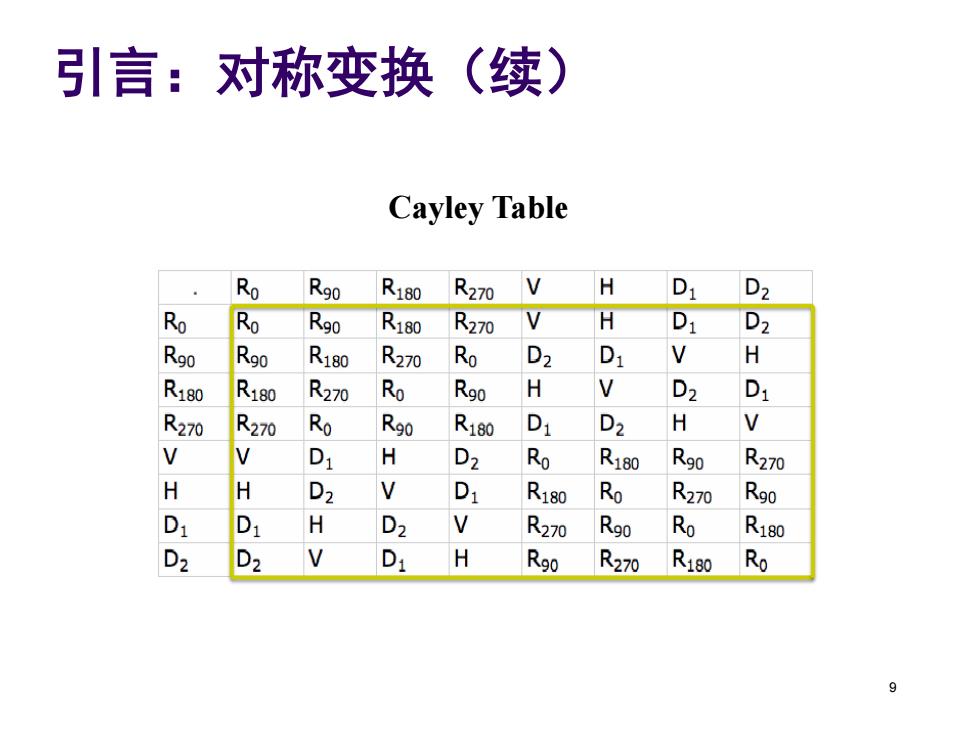
引言:对称变换(续) Cayley Table Ro Rgo R180 R270 V H D1 D2 Ro Ro Rgo R180 R270 V A D1 D2 Rgo Rgo R180 R270 Ro D2 D1 V H R180 R180 R270 Ro Rgo H V D2 Di R270 R270 Ro R9o R180 D1 D2 H N D1 H D2 Ro R180 R90 R270 H H D2 D1 R180 Ro R270 R9o H D2 V R270 R9o R R180 D2 D2 V Di H R9o R270 R180 Ro 9
引言:对称变换(续) 9 Cayley Table

引言:对称变换(续) S={Ro:R1:R2:R3:V,H,D1:D2} *为S上的两元运算 事实上可通过函数的复合来计算积。例如 Ru* -(〔2)-(a 通过运算可知 (1)*对于S是封闭的,即(c,y∈S)(x*y∈S) (2)(付c,4,之∈S)(c*(y*)=(c*y)*) (3)(付x∈S)(Ro*x=E*R0=x) (4)(x∈S)(日y∈S)(E*y=y*x=Ro) 10
引言:对称变换(续) 10