
导航 参数μ反映了正态分布的集中位置,ō反映了随机变量的分布 相对于均值μ的离散程度 实际上,我们有若X~N(4,σ2),则E(X)=,D(X=
导航 参数μ反映了正态分布的集中位置,σ反映了随机变量的分布 相对于均值μ的离散程度. 实际上,我们有若X~N(μ,σ 2 ),则E(X)= μ ,D(X)= σ 2

导月 4.3σ原则 假设X~N(,G2),可以证明:对给定的k∈N*,P(-ko≤X ≤+ko)是一个只与k有关的定值特别地, P-o≤X≤u+o P(-2o≤X≤u+2o)≈ P(u-3o≤X≤u+3G (2)在实际应用中,通常认为服从于正态分布N(4,σ2)的随机 变量X只取-3o,+3σ]中的值,这在统计学中称为3σ原则
导航 4.3σ原则 (1)假设X~N(μ,σ 2 ),可以证明:对给定的k∈N* ,P(μ-kσ≤X ≤μ+kσ)是一个只与k有关的定值.特别地, P(μ-σ≤X≤μ+σ)≈ 0.682 7 , P(μ-2σ≤X≤μ+2σ)≈ 0.954 5 , P(μ-3σ≤X≤μ+3σ)≈ 0.997 3 . (2)在实际应用中,通常认为服从于正态分布N(μ,σ 2 )的随机 变量X只取[μ-3σ,μ+3σ]中的值,这在统计学中称为3σ原则
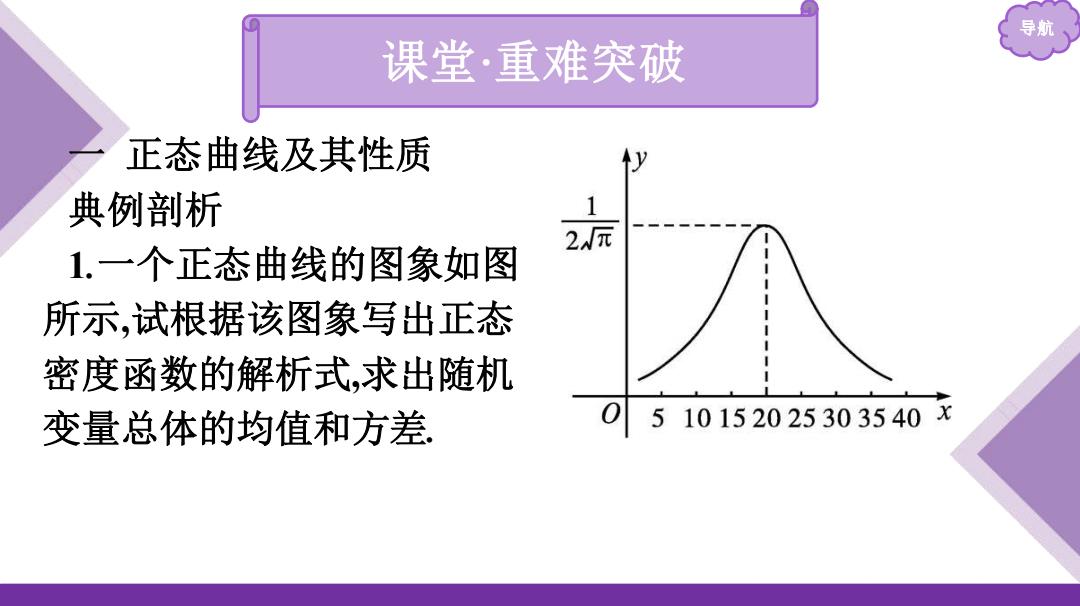
导航 课堂·重难突破 正态曲线及其性质 典例剖析 2元 1.一个正态曲线的图象如图 所示,试根据该图象写出正态 密度函数的解析式,求出随机 变量总体的均值和方差 0510152025303540 x
导航 一 正态曲线及其性质 典例剖析 1.一个正态曲线的图象如图 所示 ,试根据该图象写出正态 密度函数的解析式 ,求出随机 变量总体的均值和方差 . 课堂 ·重难突破