2.典型电路分析法 记住一些典型电路RC串 (=0 联、RL串联、RC并联、 RL并联等)的分析结果, 典型电路 在分析非典型电路时可 以设法套用。 (t=0) 3.三要素法 任意Ns 只要知道一阶电路的 三个要素,代入一个 公式就可以直接得到 重点掌握3,1、2 结果,这是分析一阶 两种方法可掌握其 电路的最有效方法。 中之一。 2025年4月2日星期三 6
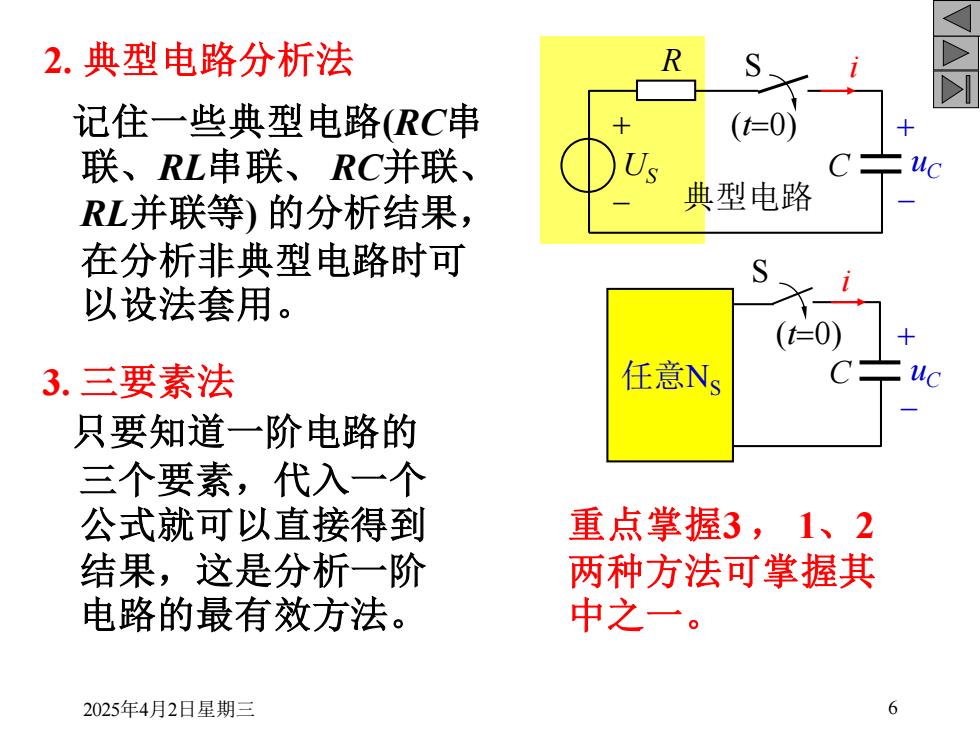
2025年4月2日星期三 6 2. 典型电路分析法 记住一些典型电路(RC串 联、RL串联、 RC并联、 RL并联等) 的分析结果, 在分析非典型电路时可 以设法套用。 3. 三要素法 只要知道一阶电路的 三个要素,代入一个 公式就可以直接得到 结果,这是分析一阶 电路的最有效方法。 任意NS C uC + - i S (t=0) S US + - (t=0) + - uC R C i 典型电路 重点掌握3 , 1、2 两种方法可掌握其 中之一
二、换路及换路定则 1.换路 电路结构或元件参数的改变称为 12V =0 换路。换路是在=0(或t=t)时 82 刻进行的。 纯电阻电路在换路时没有过渡期。 (t=0) 22 含有动态元件的电路换 路时存在过渡过程,过 24V 渡过程产生的原因是由 42 于储能元件L、C,在换 路时能量发生变化,而 能量的储存和释放需要一定的时间来完成。 2025年4月2日星期三
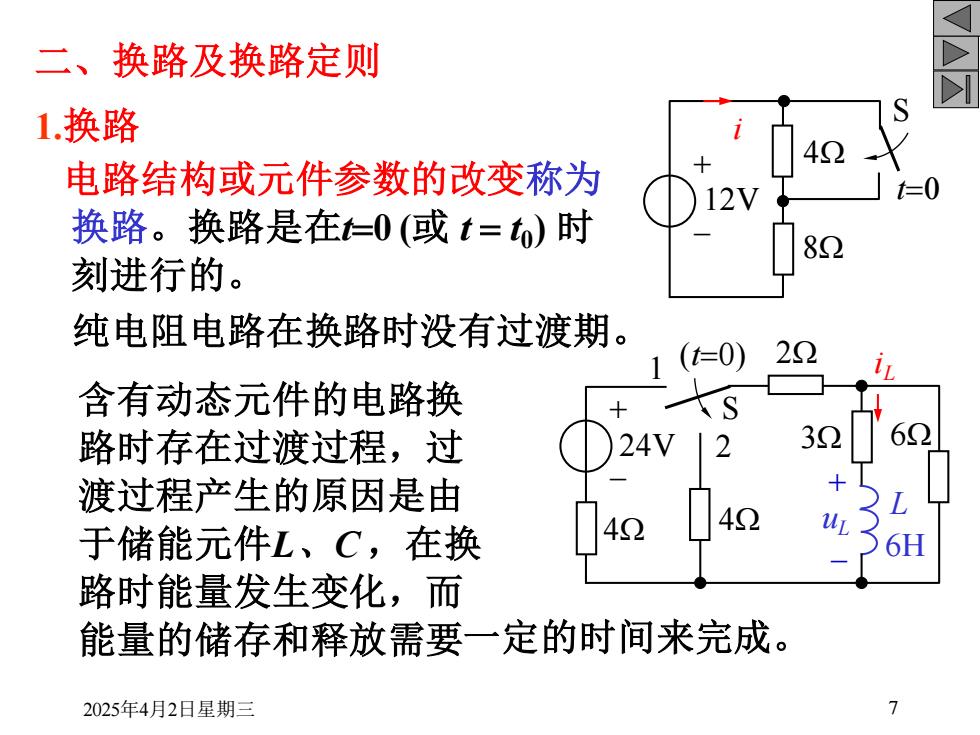
2025年4月2日星期三 7 二、换路及换路定则 1.换路 电路结构或元件参数的改变称为 换路。换路是在t=0 (或 t = t0 ) 时 刻进行的。 含有动态元件的电路换 路时存在过渡过程,过 渡过程产生的原因是由 于储能元件L、C ,在换 路时能量发生变化,而 能量的储存和释放需要 S 24V + - (t=0) + L iL 4W 1 4W 2 2W 3W 6H 6W - uL 12V + - i 8W 4W t=0 S 纯电阻电路在换路时没有过渡期。 一定的时间来完成

2.换路定则 线性电容C的电荷g0=6)+c(⑤d5 以t=t=0作为换路的计时起点:换路前最终时 刻记为t=0_,换路后最初时刻记为t=0+。 在换路前后:0=0)+5时 0_到0瞬间,ic)为有限值时,积分为0。 q(0+)=q0-) C上的电荷不能跃变! 由q(①=Cuc()可知,当换路前后C不变时 uc0+)=uc(0)C两端的电压也不能跃变! 2025年4月2日星期三 8
2025年4月2日星期三 8 2. 换路定则 在换路前后: q(t) = q(t0 ) +∫ t t0 iC (x) dx q(0+ ) = q(0- ) + 0+ 0- iC(x) dx 以t = t0 = 0作为换路的计时起点:换路前最终时 刻记为t = 0-,换路后最初时刻记为t = 0+。 线性电容C的电荷 0-到0+瞬间,iC(t)为有限值时,积分为0。 q(0+ ) = q(0- ) C上的电荷不能跃变! 由q(t) = C uC(t)可知,当换路前后C不变时 uC(0+ ) = uC(0- ) C两端的电压也不能跃变!

q(0+)=q(0) uc(0+)=uc(0)) 同理可得: Ψ(0)=Ψ(0)》 L中的磁链不能跃变! 由Ψ()=Li()可知,当换路前后L不变时 iz(0)=z(0) L中的电流也不能跃变! 换路定则表明 ()换路瞬间,若电容电流保持为有限值,则电 容电压(电荷)在换路前后保持不变,这是 电荷守恒定律的体现。 (2)换路瞬间,若电感电压保持为有限值,则电 感电流(磁链)在换路前后保持不变。这是 磁链守恒定律的体现。 2025年4月2日星期三 9
2025年4月2日星期三 9 Y (0+ ) =Y (0- ) L中的磁链不能跃变! 由Y (t) = LiL (t) 可知,当换路前后L不变时 iL (0+ ) = iL (0- ) L中的电流也不能跃变! q(0+ ) = q(0- ) uC(0+ ) = uC(0- ) 同理可得: 换路定则表明 (1)换路瞬间,若电容电流保持为有限值,则电 容电压(电荷)在换路前后保持不变,这是 电荷守恒定律的体现。 (2)换路瞬间,若电感电压保持为有限值,则电 感电流(磁链)在换路前后保持不变。这是 磁链守恒定律的体现

换路定则 设:仁0一表示换路瞬间(定为计时起点) 仁O.一表示换路前的终了瞬间 t仁0+一表示换路后的初始瞬间(初始值) 电感电路:iz(0+)=iz(0_) 电容电路:hc(0+)=uc(0_) 注:换路定则仅用于换路瞬间来确定暂态过程中 uc、初始值。 2025年4月2日星期三 10
2025年4月2日星期三 10 电容电路: (0 ) (0 ) uC + = uC - 注:换路定则仅用于换路瞬间来确定暂态过程中 uC、 iL初始值。 设:t=0 — 表示换路瞬间 (定为计时起点) t=0-— 表示换路前的终了瞬间 t=0+—表示换路后的初始瞬间(初始值) 换路定则 电感电路: (0 ) (0 ) L + = L -