
2.KVL的独立方程数 KVL的独立方程数=基本回路数=b一(n一1) 结论 n个结点、b条支路的电路,独立的 KCL和KVL方程数为: (n-1)+b-(n-1)=b
2.KVL的独立方程数 KVL的独立方程数=基本回路数=b-(n-1) 结 论 n个结点、b条支路的电路, 独立的 KCL和KVL方程数为: (n 1) b (n 1) b

3.3支路电流法 (branch current method 1.支路电流法 以各支路电流为未知量列写电路方 程分析电路的方法。 对于有个节点、b条支路的电路,要求解支路电 流,未知量共有b个。只要列出b个独立的电路方程,便 可以求解这b个变量。 2.独立方程的列写 (1)从电路的n个结点中任意选择n-1个结点列写KCL方程 (2)选择基本回路列写b-(n-1)个KVL方程
3.3 支路电流法 (branch current method ) 对于有n个节点、b条支路的电路,要求解支路电 流,未知量共有b个。只要列出b个独立的电路方程,便 可以求解这b个变量。 以各支路电流为未知量列写电路方 程分析电路的方法。 1. 支路电流法 2. 独立方程的列写 (1)从电路的n个结点中任意选择n-1个结点列写KCL方程 (2)选择基本回路列写b-(n-1)个KVL方程

§3-3 支路电流法 一、2b法 对于有n个节点、b条支路的电路, a每条支路 b个VCR方程 b.n个结点 (n-1)个独立的KCL方程 2 c回路 b-(-1)个KVL方程 举例说明: b=6 n=4 R6 十 us
§33 支路电流法 一、2b法 对于有n个节点、b条支路的电路, a. 每条支路 c. 回路 b个VCR方程 b. n个结点 (n–1)个独立的KCL方程 b–(n–1)个KVL方程 举例说明: R1 R2 R3 R4 R5 R6 + – i2 i3 i4 i1 i5 i6 uS 1 2 3 4 b=6 n=4
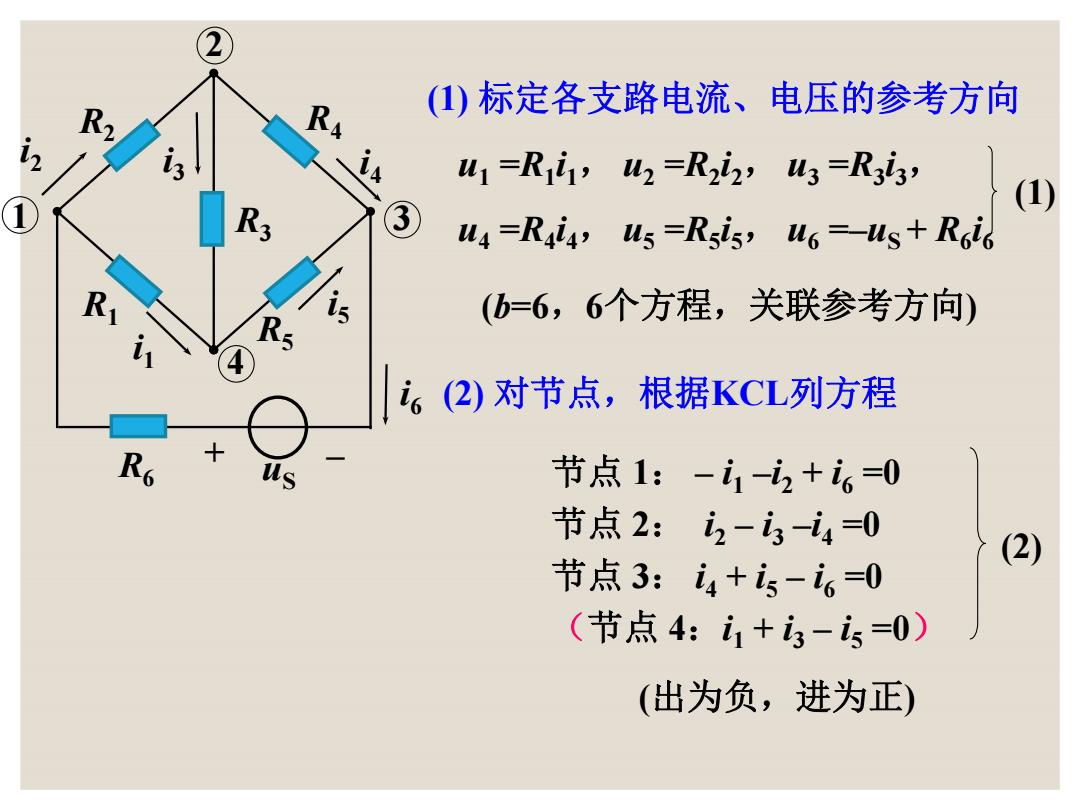
()标定各支路电流、电压的参考方向 儿1=R1i1,W2=R2i2,W3=R33? (1) 3 us=Rais,us =Rsis,u6=us+Roi R (b=6,6个方程,关联参考方向) i6(2)对节点,根据KCL列方程 R6 us 节点1:-i1-i2+6=0 节点2:2-3-i4=0 (2) 节点3:i4+i5-6=0 (节点4:i1+3-i5=0) (出为负,进为正)
R1 R2 R3 R4 R5 R6 + – i2 i3 i4 i1 i5 i6 uS 1 2 3 4 (1) 标定各支路电流、电压的参考方向 u1 =R1 i1, u2 =R2 i2, u3 =R3 i3, u4 =R4 i4, u5 =R5 i5, u6 =–uS + R6 i6 (1) (b=6,6个方程,关联参考方向) (2) 对节点,根据KCL列方程 节点 1: – i1 –i2 + i6 =0 节点 2: i2 – i3 –i4 =0 节点 3: i4 + i5 – i6 =0 (节点 4:i1 + i3 – i5 =0) (2) (出为负,进为正)
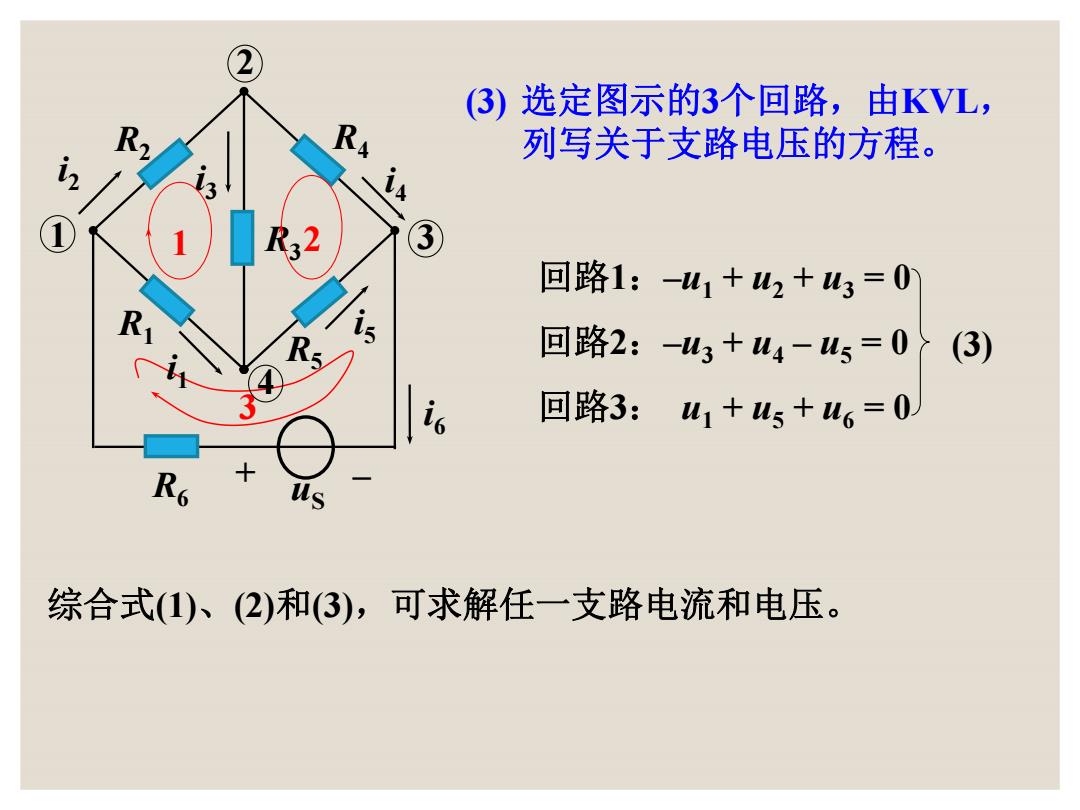
2 (3)选定图示的3个回路,由KVL, 列写关于支路电压的方程。 2 ▣路1:-w1+u2+W3=0 回路2:-3+u4-W5=0 (3) 6 回路3:u1+45+u6=0 R6 us 综合式(1)、(2)和(3),可求解任一支路电流和电压
3 R1 R2 R3 R4 R5 R6 + – i2 i3 i4 i1 i5 i6 uS 1 2 3 4 (3) 选定图示的3个回路,由KVL, 列写关于支路电压的方程。 回路1:–u1 + u2 + u3 = 0 回路2:–u3 + u4 – u5 = 0 回路3: u1 + u5 + u6 = 0 (3) 1 2 综合式(1)、(2)和(3),可求解任一支路电流和电压