
基本回路(单连支回路) 基本回路具有独占的一条连枝 结论 支路数=树枝数+连支数 =结点数一1+基本回路数 结点、支路和 基本回路关系 b=n+1-1
基本回路(单连支回路) 1 2 3 4 5 6 5 1 2 3 1 2 3 6 支路数=树枝数+连支数 =结点数-1+基本回路数 结论 b n l 1 结点、支路和 基本回路关系 基本回路具有独占的一条连枝
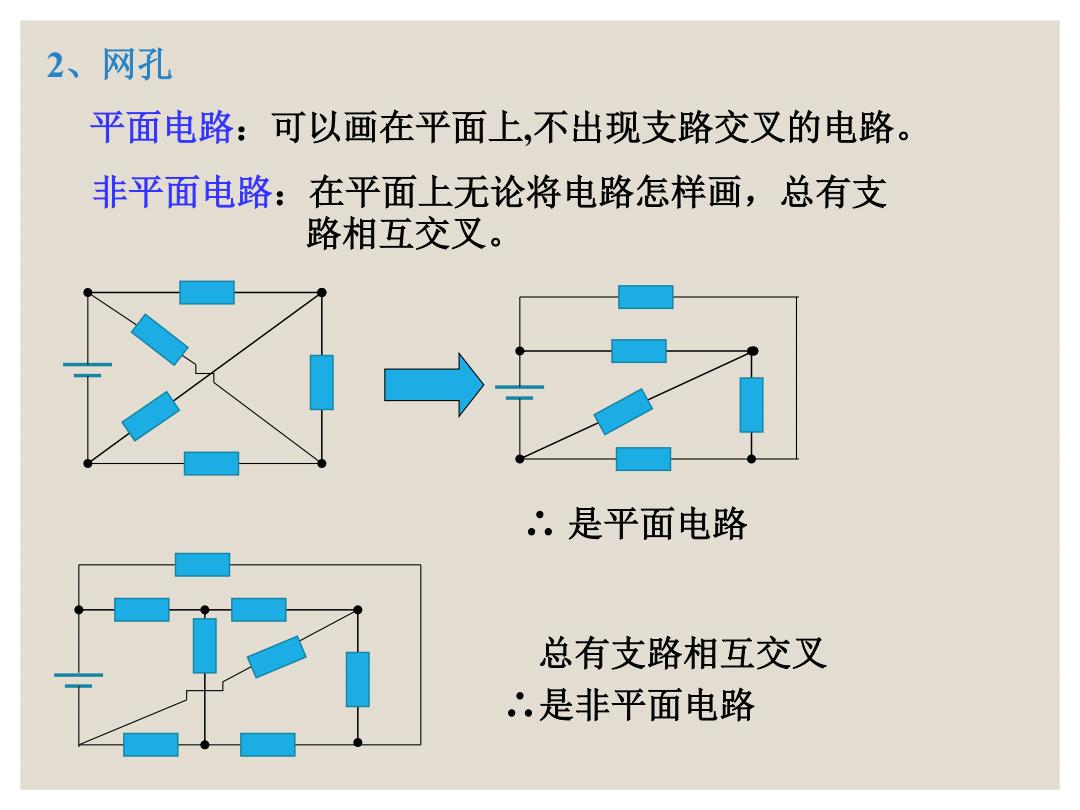
2、网孔 平面电路:可以画在平面上,不出现支路交叉的电路。 非平面电路:在平面上无论将电路怎样画,总有支 路相互交叉。 .是平面电路 总有支路相互交叉 ∴是非平面电路
2、网孔 平面电路:可以画在平面上,不出现支路交叉的电路。 非平面电路:在平面上无论将电路怎样画,总有支 路相互交叉。 ∴ 是平面电路 总有支路相互交叉 ∴是非平面电路

网孔: 平面图的一个“网孔”是指它的一个自然“孔”,它限定 的区域内不再含有支路; 平面图的全部网孔是一组独立回路; 平面图网孔数=独立回路数。 3、KVL的独立方程数=独立回路数 平面电路:找网孔,对网孔列方程; 非平面电路:先找树,再找单连支回路, 对单连支回路列方程; 可以证明:对于有n个结点,b条支路的电路, 可以列出b-(-1)个独立的KVL方程
平面图的全部网孔是一组独立回路; 平面图网孔数 = 独立回路数。 网孔: 平面图的一个“网孔”是指它的一个自然“孔” ,它限定 的区域内不再含有支路; 3、KVL的独立方程数 非平面电路:先找树,再找单连支回路, 对单连支回路列方程; = 独立回路数 平面电路: 找网孔,对网孔列方程; 可以证明: 对于有n个结点,b条支路的电路, 可以列出b–(n–1)个独立的KVL方程
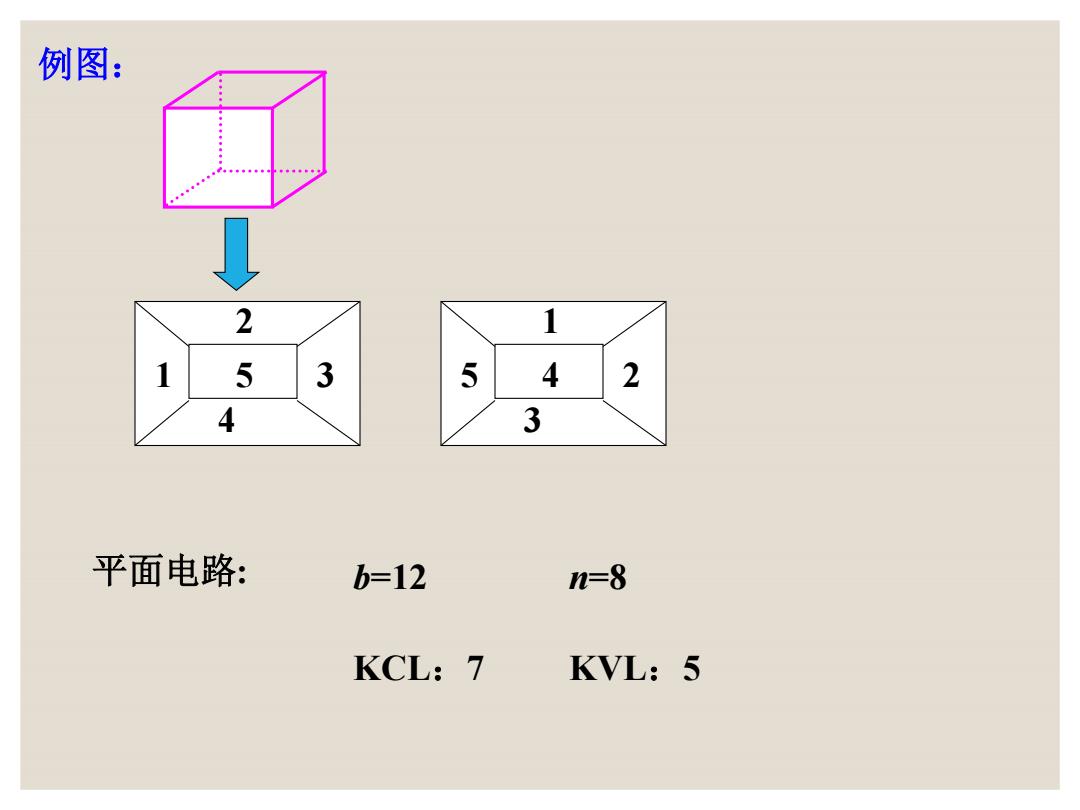
例图: 2 1 1 5 3 5 4 2 4 3 平面电路: b=12 n=8 KCL:7 KVL:5
例图: 1 4 5 3 2 5 3 4 2 1 平面电路: b=12 n=8 KCL:7 KVL:5

小结:KCL和KVL的独立方程数 1.KCL的独立方程数 i-i4-i6=0 2 -i-i2+i3=0 3 i2+i+i6=0 4 -i3+i4-i=0 +2十3+4=0 结论 n个结点的电路,独立的KCL方程为n-1个
小结: KCL和KVL的独立方程数 1.KCL的独立方程数 0 i 1 i 4 i 6 6 5 4 3 2 1 4 3 2 1 1 4 3 2 0 i 3 i 4 i 5 0 i 2 i 5 i 6 0 i 1 i 2 i 3 1 + 2 + 3+ 4 =0 结论 n个结点的电路, 独立的KCL方程为n-1个