
第八章第九章 要点:1.正弦量的基本概念:三要素、相位差、波 形. 2.定量计算:相量法 辅助工具:相量图 3功率计算:有功、无功、视在功率、功率因数、 复功率等
第八章 第九章 要点:1. 正弦量的基本概念:三要素、相位差、波 形… 2. 定量计算:相量法 辅助工具:相量图 3.功率计算:有功、无功、视在功率、功率因数、 复功率等

一.正弦量、相量的基本概念 左图电路中,已知: 1、 u(t)=10cos(400元t+60°)V L 0z=|z∠9 0)=2 in(400πt-150°)A (a)电源电压角频率o=400元rad/s,频率=200Hz,周期T=0.005s (b)电压有效值U=7.07V,电流有效值= 0.5A (c)电压、电流间相位差平。平,=120 (d该负载是感性负载,☑=14.142 ,9= 120°
一. 正弦量、相量的基本概念 左图电路中,已知: sin( 400π 150 ) A 2 1 ( ) ( ) 10 cos(400 60 ) V i t t u t πt 1、 400 rad/s 200Hz 0.005s 7.07V 0.5A 120 感性 14.14 i + u Z Z φ – (a)电源电压角频率 =_________ , 频率 f=_____ , 周期 T=_______. (b)电压有效值U=_______,电流有效值 I=________. (c)电压、电流间相位差 u– i =_________. (d)该负载是______负载, |Z|=_________, =_________. 120
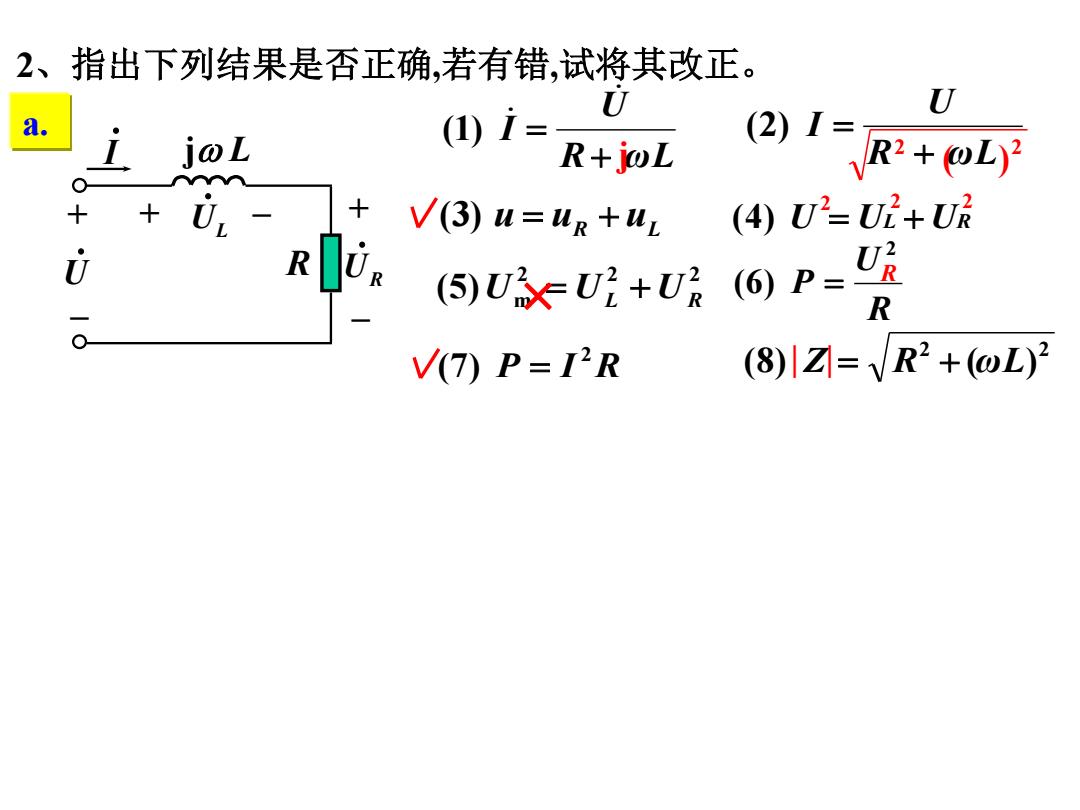
2、指出下列结果是否正确,若有错,试将其改正。 U U a. i (1)1= R+j@L 21=R2+ob 十 V(3)u=uR+uL (4)U2=U+UR R U: (⑤)UxU2+UR(⑥)P= R V(7)P=IR (8)川☑=VR+@L)2
2、指出下列结果是否正确,若有错,试将其改正。 R ωL U I (1) (2) R ωL U I u uR uL (3) (4) U UL UR 2 2 2 m (5)U UL UR R U P 2 (6) P I R 2 (7) 2 2 (8) Z R (ωL) a. R 2 2 2 j R j L + – U I UL + – + – UR 2 2 ( ) | |
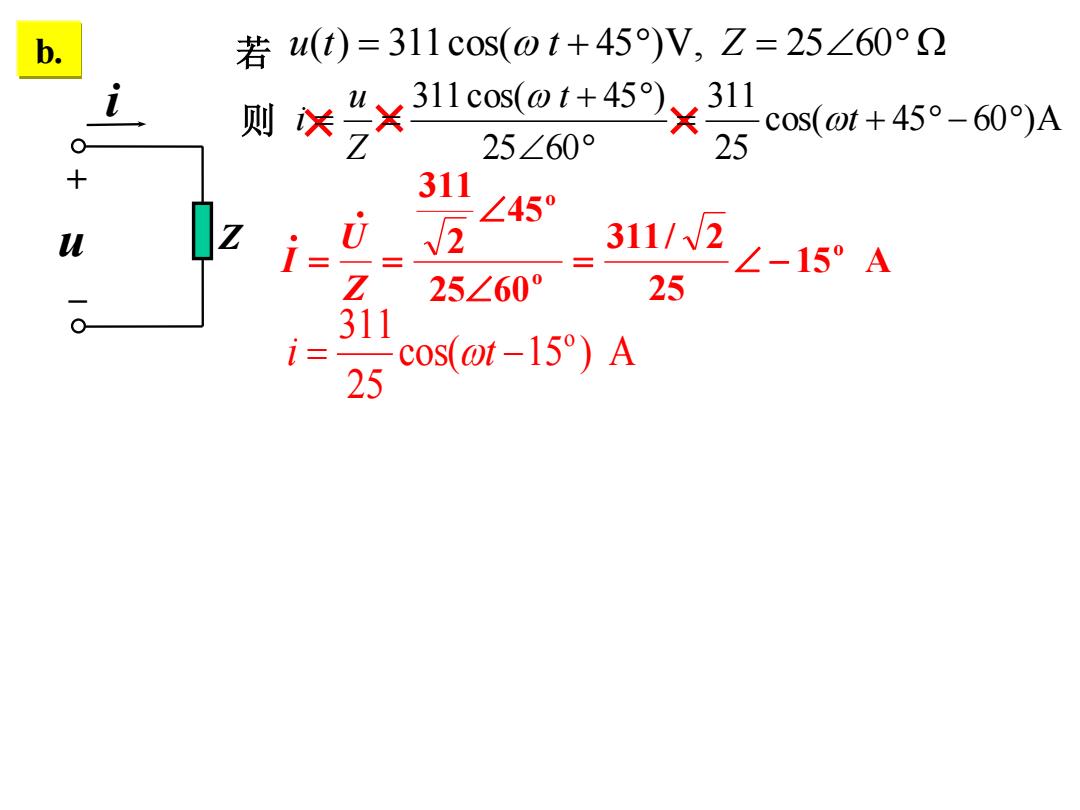
b. 若u(t)=311c0s(0t+45)V,Z=25∠60°2 则关 + 11c0s(ot+45)、311 -C0s(ot+45°-60)A 25∠60° 25 + 311 ∠45° L Z i 311/V2 一 ∠-15°A 25∠60° 25 311 i= cos(@t-15)A 25
若 u(t) 311cos( t 45 )V, Ζ 25 60 Ω 则 b. cos( 45 60 )A 25 311 25 60 311cos( 45 ) t t Zu i u Z i +– 15 A 25 311/ 2 25 60 45 2 311 o o o ZU I cos( 15 ) A 25 311 o i t

用相量法分析正弦稳态电路的基本步骤: ()时域电路-〉相量模型 a:u,i的相量形式 b:各元件的阻抗 根据电路的结构特点,选用合适的分析方法,求出待求变量 的相量 根据求得的相量,写出其时域表达式
用相量法分析正弦稳态电路的基本步骤: (1) 时域电路--------〉相量模型 a:u,i 的相量形式 b:各元件的阻抗 • 根据电路的结构特点,选用合适的分析方法,求出待求变量 的相量 • 根据求得的相量,写出其时域表达式