
例 一容器内某理想气体的温度为273K,密度为p=1.25gm3, 压强为p=1.0×10-3atm 求()气体的摩尔质量,是何种气体? (2)气体分子的平均平动动能和平均转动动能? (3)单位体积内气体分子的总平动动能? (4设该气体有0.3mol,气体的内能? 解①由pV=mR7,有 M M=pR7_125×103x8.31x273 =0.028 kg/mol p 103×1.013×10 由结果可知,这是N2或CO气体
一容器内某理想气体的温度为273K,密度为ρ= 1.25 g/m3 , 压强为 p = 1.0×10-3 atm (1) 气体的摩尔质量,是何种气体? (2) 气体分子的平均平动动能和平均转动动能? (3) 单位体积内气体分子的总平动动能? (4) 设该气体有0.3 mol,气体的内能? 解 例 求 0.028 kg/mol 10 1.013 10 1.25 10 8.31 273 3 5 3 = = = − − p RT M 由结果可知,这是N2或CO 气体。 (1) 由 RT ,有 M m pV =

(2)平均平动动能和平均转动动能为 6=3k知=3×138×102×273=556×102] 8=kT=1.38×1023×273=3.77×1021J (③)单位体积内气体分子的总平动动能为 =6m=8,分为 元=5.56×1021× 1.013×102 138×10-23×273 =1:52×102J/m (4④由气体的内能公式,有 5 E= ".'R7=0.3××8.31×273=1.70×10J M 2
(2) 平均平动动能和平均转动动能为 1.38 10 273 5.56 10 J 2 3 2 3 −23 −21 t = kT = = 1.38 10 273 3.77 10 J −23 −21 r = kT = = (3) 单位体积内气体分子的总平动动能为 2 3 23 2 21 1.52 10 J/m 1.38 10 273 1.013 10 5.56 10 = = = = − − kT p Et t n t 8.31 273 1.70 10 J 2 5 0.3 2 3 = RT = = i M m E (4) 由气体的内能公式,有

§12.8玻耳兹曼分布律 问题: 麦克斯韦速率分布律是关于无外力场时,气体分子 的速率分布。此时,分子在空间的分布是均匀的。 若有外力场存在,分子按密度如何分布呢? 一,重力场中粒子按高度的分布 dp=-pgdh p+dp dp =-nugdh h+dh 平衡态下气体的温度处处 dh 相同,气体的压强为 p=nkT p dp kTdn 非均匀的稳定分布)
§12.8 玻耳兹曼分布律 一. 重力场中粒子按高度的分布 麦克斯韦速率分布律是关于无外力场时,气体分子 的速率分布。此时,分子在空间的分布是均匀的。 若有外力场存在,分子按密度如何分布呢? 问题: (非均匀的稳定分布) 平衡态下气体的温度处处 相同,气体的压强为 p = nkT p + dp p dh dp = − gdh dp = kTdn dp = −n gdh h h+dh
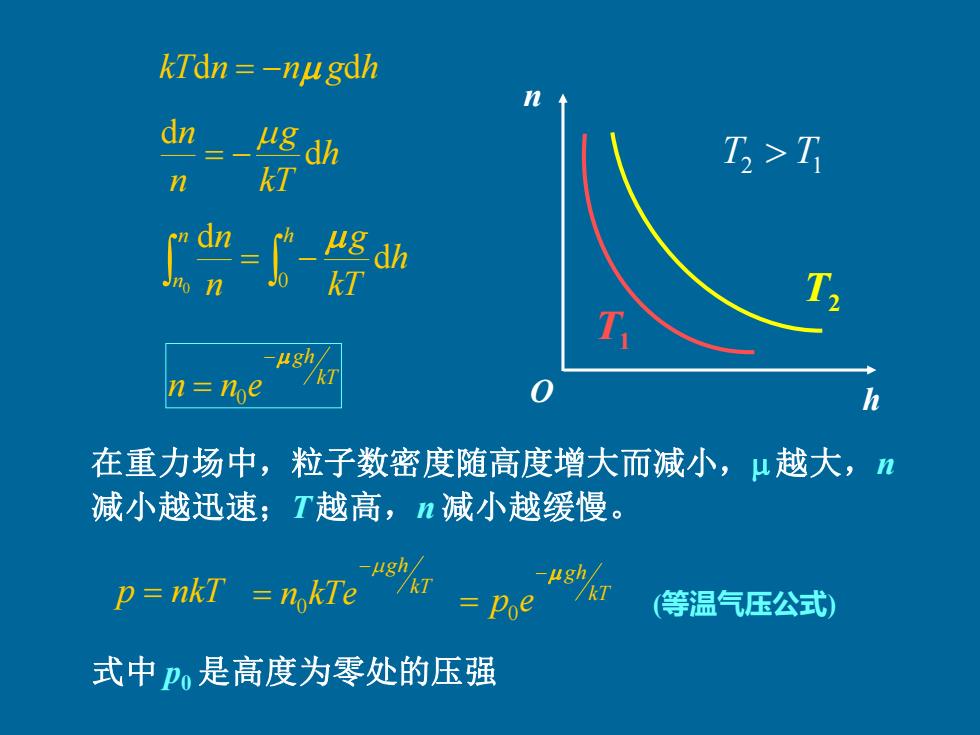
kTdn=-nugdh dn ug dh D>T n kT 1g dh kT ugh/ n noe 在重力场中,粒子数密度随高度增大而减小,μ越大,n 减小越迅速;T越高,n减小越缓慢。 gh☑ p=nkT =nkTe /kr gh☑ =Poe k7 (等温气压公式) 式中p,是高度为零处的压强
kTdn = −n gdh h kT g n n d d = − = − n h n h kT g n n 0 d d 0 kT gh n n e − = 0 p = nkT kT gh p e − = 0 O h n T2 T1 T2 T1 kT gh n kTe − = 0 在重力场中,粒子数密度随高度增大而减小, 越大,n 减小越迅速;T 越高,n 减小越缓慢。 (等温气压公式) 式中 p0 是高度为零处的压强

例 实验测得常温下距海平面不太高处,每升高10,大气压 约降低133.3Pa。试用恒温气压公式验证此结果(海平面 上大气压按1.013×105Pa计,温度取273K)。 解等温气压公式 p=Poe=poe 将上式两边微分,有 p=poe( Mgdh dp Mg dh RT RT RT AP 8.31×273 -133.3 △h =10.3m Mg p 28.97×103×101.013×10
实验测得常温下距海平面不太高处,每升高10 m,大气压 约降低133.3 Pa。试用恒温气压公式验证此结果(海平面 上大气压按1.013×105 Pa 计,温度取273K)。 p p Mg RT h − 3 5 1.013 10 133.3 28.97 10 10 8.31 273 − = − − =10.3m 解 例 gh kT Mgh RT p p e p e / 0 / 0 − − = = ) d d ( 0 RT Mg h p p e Mgh RT = − − h RT Mg p p d d = − 等温气压公式 将上式两边微分,有