
S1.4初等矩阵 定义8.1.4 由单位矩阵E经过一次初等变换所得的矩阵称为初等矩阵 注:三种初等变换对应有三种初等矩阵 门),第一类初等矩购 EED)= 张鞘同济大学 8/37
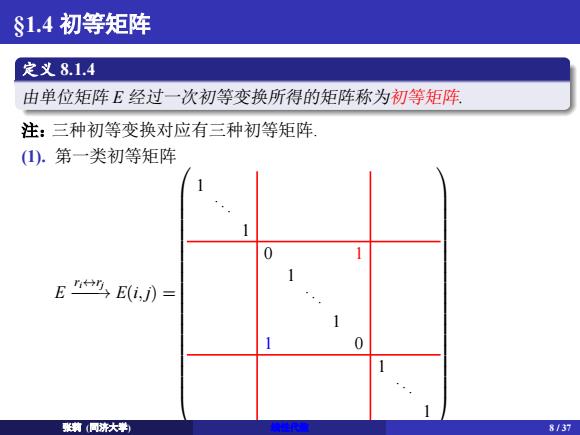
§1.4 初等矩阵 . 定义 8.1.4 . .由单位矩阵 E 经䗷一次初等变换所得的矩阵称为初等矩阵. 注:三种初等变换对应有三种初等矩阵. (1). 第一类初等矩阵 E ri↔rj −−−→ E(i, j) = . 1. . . . . . . . . . . . . . . . . . . . . . . . . . . 1. . . . . . . . . . . . 0. . . . 1. . . . . . . . 1. . . . . . . . . . . . . . . . . . . . . . . . . . . 1. . . . . . . . 1. . . . 0. . . . . . . . . . . . 1. . . . . . . . . . . . . . . . . . . . . . . . . . . 1. . . ᕖ㦿 (ੂ⎄ཝᆜ) 线性ԙᮦ 8 / 37
S1.4初等矩阵 定义8.1.4 由单位矩阵E经过一次初等变换所得的矩阵称为初等矩阵 注:三种初等变换对应有三种初等矩阵 (1).第一类初等矩阵 0 EeE(i,1)= 0 张鞘同济大学 8/37
§1.4 初等矩阵 . 定义 8.1.4 . .由单位矩阵 E 经䗷一次初等变换所得的矩阵称为初等矩阵. 注:三种初等变换对应有三种初等矩阵. (1). 第一类初等矩阵 E ri↔rj −−−→ E(i, j) = . 1. . . . . . . . . . . . . . . . . . . . . . . . . . . 1. . . . . . . . . . . . 0. . . . 1. . . . . . . . 1. . . . . . . . . . . . . . . . . . . . . . . . . . . 1. . . . . . . . 1. . . . 0. . . . . . . . . . . . 1. . . . . . . . . . . . . . . . . . . . . . . . . . . 1. . . ᕖ㦿 (ੂ⎄ཝᆜ) 线性ԙᮦ 8 / 37

2).第二类初等矩阵 E nxk E(i(k))= 张纳同济大学 性物 9/37
(2). 第二类初等矩阵 E ri×k −−→ E ( i ( k)) = . 1. . . . . . . . . . . . . . . . . . . 1. . . . . . . . k. . . . . . . . 1. . . . . . . . . . . . . . . . . . . 1. . . ᕖ㦿 (ੂ⎄ཝᆜ ) 线性ԙᮦ 9 / 37

3).第三类初等矩阵 E(ij(k)= (初等变换有6类,初等矩阵只有3类) 张鞘同济大学 10/37
(3). 第三类初等矩阵 E ri+k×rj −−−−→ E (ij ( k)) = . 1. . . . . . . . . . . . . . . . . . . . . . . 1. . . . . . . . . . 1. . k. . . . . . . . . . . . . . . . . . . . . 1. . . . . . . . . . 1. . . . . . . . . . . . . . . . . . . . . . . 1. . . (初等变换有 6 类,初等矩阵只有 3 类 ) ᕖ㦿 (ੂ⎄ཝᆜ ) 线性ԙᮦ 10 / 37

§初等矩阵的若干理论应用 性质8.1.1 对A施行一次初等行或列变换,相当于A左乘(或右乘)此初等变换所对 应的初等矩阵 性质8.12 订等矩阵均可道,且有 0E10-1=E ●E((0)厂1=E( ●E(-=E(7(-) 张鞘同济大学 11/37
§ 初等矩阵的若干理论应用 . . 性质 8.1.1 . . 对 A 施行一次初等行 (或列) 变换,相当于 A 左乘 (或右乘) 此初等变换所对 应的初等矩阵. . 性质 8.1.2 . . 初等矩阵均可逆,且有 .1 E(i, j) −1 = E(i, j) .2 E(i(k))−1 = E(i( 1 k )) 3. E(ij(k))−1 = E(ij(−k)) . 性质 8.1.3 . .初等变换؍ᤱ矩阵的可逆性. 䇷: 可逆方阵 (左、右) 乘初等矩阵后仍可逆. ᕖ㦿 (ੂ⎄ཝᆜ) 线性ԙᮦ 11 / 37