
第四章正弦交流电路 一、内容提要 本章主要讨论正弦交流电的基本概念和基本表示方法,并从分析R人、C各单一参数元 件在交流电路中的作用入手,进而分析一般的R、人、C混联电路中电压和电流的关系(包括 数值和相位) 率转换问。最后对于电路中串联和并联的谐振现象也作概搭的 述 交流电路不仅是交流电机和变压器的理论基础,同时也要为电子电路做好理论准备,它 是工程技术科学研究和日常生活中经常碰到的。所以本章是本课程中重要的内容之一。 二、基本要求 1、对正弦交流电的产生作一般了解: 2、掌握正弦交流电的概念: 3、准确理解正弦交流电的三要素、相位差及有效值的定义及表达式: 4、掌握正弦交流电的各种表示方法及相互间的关系: 在掌握单一参数交流电路的基础上,重点掌握R人、C串、并联电路的分析与计算 方法: 7、掌握有用功功率和功率因数的计算,了解解时功率、无功功率、视在功率的概念 8、理解提高功率因数的意义:掌握如何提高功率因数: 9、了解诰振电路的特性。 三、学习指导 1,正弦量的参考方向和相位 1)、大小和方向随时间按正弦函数规律变化的电流或电压称为正弦交流电。正弦交流电 的参考方向为其正半周的实际方向。 2)、正弦交流电的三要素 一个正弦量是由频率(或周期)、幅值(或有效值)和初相位三个要素来确定。 (1)频率与周期:正弦量变化一次所需的时间(S)称为周期T。每秒内变化的次数称 为频率人,单位:H,·频率与周期的关系为:了= 角频率:每秒变化的弧度,单位:ads。 (2)幅值与有效值 瞬时值:正弦量在任一时刻的值,用e,4,i表示。 幅值(或最大值):瞬时值中的最大值,用Em,Um,I表示。 有效值:一个周期内,正弦量的有效值等于在相同时间内产生相同热量的直流电量值, 用E,U,I表示
1 第四章 正弦交流电路 一、内容提要 本章主要讨论正弦交流电的基本概念和基本表示方法,并从分析 R、L、C 各单一参数元 件在交流电路中的作用入手,进而分析一般的 R、L、C 混联电路中电压和电流的关系(包括 数值和相位)及功率转换问题。最后对于电路中串联和并联的谐振现象也作概括的论述。 交流电路不仅是交流电机和变压器的理论基础,同时也要为电子电路做好理论准备,它 是工程技术科学研究和日常生活中经常碰到的。所以本章是本课程中重要的内容之一。 二、基本要求 1、对正弦交流电的产生作一般了解; 2、掌握正弦交流电的概念; 3、准确理解正弦交流电的三要素、相位差及有效值的定义及表达式; 4、掌握正弦交流电的各种表示方法及相互间的关系; 5、熟悉各种交流电气元件及才参数; 6、在掌握单一参数交流电路的基础上,重点掌握 R、L、C 串、并联电路的分析与计算 方法; 7、掌握有用功功率和功率因数的计算,了解瞬时功率、无功功率、视在功率的概念 8、理解提高功率因数的意义;掌握如何提高功率因数; 9、了解谐振电路的特性。 三、 学习指导 1. 正弦量的参考方向和相位 1)、大小和方向随时间按正弦函数规律变化的电流或电压称为正弦交流电。正弦交流电 的参考方向为其正半周的实际方向。 2)、正弦交流电的三要素 一个正弦量是由频率(或周期)、幅值(或有效值)和初相位三个要素来确定。 (1)频率与周期:正弦量变化一次所需的时间(S)称为周期 T。每秒内变化的次数称 为频率f,单位: HZ 。频率与周期的关系为: T f 1 = 角频率 :每秒变化的弧度,单位: rad /s 。 f T 2 2 = = (2)幅值与有效值 瞬时值:正弦量在任一时刻的值,用 e,u,i 表示。 幅值(或最大值):瞬时值中的最大值,用 m m m E ,U ,I 表示。 有效值:一个周期内,正弦量的有效值等于在相同时间内产生相同热量的直流电量值, 用 E,U,I 表示

幅值与有效值关系:Em=V2E,Um=V2U,1m=21 注意:符号不能混用。 (3)初相位:正弦量的相位(+?,)是反映正弦量变化进程的,初相位用来确定正 弦量的初始值。画波形图时,如果初相位为正角,t0时的正弦量值应为正半周,从t=0点 向左,到向负值增加的零值点之间的角度为初相位的大小:如果初相位为负角,t=0时的正 弦量值应在负半周 从0向右,到向正值增加的零值点之间的角度为初相位的大小。 相位差:两个同频率的正弦量的相位之差等于初相位之差。 0=01-0 2.相量表示 否则,不可以用:只有同频率的正弦量才能画在同 起则无法进行比较与计算的。 3.“j”的数学意义和物理意义 )、数学意义:了=√是虚数单位 2》、物理意义:了是旋转90°的算符,即任意一个相量乘以士j后,可使其旋转士90度。 4.电压与电流间的关系 各种形式的电压与电流间的关系式,是在电压、电流的关联方向下列出的,否则,式中 带负号 5。RL、C串联电路中,当R≠0时,X,与Xc的大小对于电路的性质有一定影响。 1)、当X1>Xc,则U1>Uc,0>0电路中的电流将滞后于电路的端电压(感性电 路): 2)、当X,<Xc,则U<Uc,p=0,电路中的电流将超前于电路的端电压(容性 电路) 6.RL、C并联电路 在R【、C并联电路中,当电路的参数和电源的频率使得: 路) 。时,则1L<1。,p<0,电路的总电流超前于电路的端电压(容性电 路) 8小、时则==0电路的总电流与电路的瑞电压同相(电阻性
2 幅值与有效值关系: E E U U I I m = 2 , m = 2 , m = 2 。 注意:符号不能混用。 (3)初相位:正弦量的相位( i t + )是反映正弦量变化进程的,初相位用来确定正 弦量的初始值。画波形图时,如果初相位为正角,t=0 时的正弦量值应为正半周,从 t=0 点 向左,到向负值增加的零值点之间的角度为初相位的大小;如果初相位为负角,t=0 时的正 弦量值应在负半周 ,从 t=0 向右,到向正值增加的零值点之间的角度为初相位的大小。 相位差:两个同频率的正弦量的相位之差等于初相位之差。 =1 −2 2. 相量表示 应注意:相量只能表示正弦量,而不能等于正弦量。只有正弦周期量才能用相量表示, 否则,不可以用;只有同频率的正弦量才能画在同一向量图上,否则,不可以。倘若画在一 起则无法进行比较与计算的。 3.“j”的数学意义和物理意义 1)、数学意义: j = −1 是虚数单位 2)、物理意义:j 是旋转 0 90 的算符,即任意一个相量乘以±j 后,可使其旋转±90 度。 4. 电压与电流间的关系 各种形式的电压与电流间的关系式,是在电压、电流的关联方向下列出的,否则,式中 带负号。 5. R、L、C 串联电路中,当 R≠O 时, XL 与 X C 的大小对于电路的性质有一定影响。 1)、当 XL X C ,则 UL UC, 0 电路中的电流将滞后于电路的端电压(感性电 路); 2)、当 XL X C ,则 UL UC , = 0 ,电路中的电流将超前于电路的端电压(容性 电路) 6. R、L、C 并联电路 在 R、L、C 并联电路中,当电路的参数和电源的频率使得; 1)、 L C 1 1 X X 时,则 L C I I , 0 ,电路的总电流滞后于电路的端电压(感性电 路) 2)、 L C 1 1 X X 时,则 L C I I , 0 ,电路的总电流超前于电路的端电压(容性电 路); 3)、 L C 1 1 X X = 时,则 L C I = I , = 0 ,电路的总电流与电路的端电压同相(电阻性

电路)一并联谐振 7.在人、C电路中,如何选择参考相量 般情况下,选公共量或己知量作为参考相量,比如在、【、C串联电路中通常选电流 作为参考相量:在R、L、C并联电路中,通常选电压作为参考相量。但在已知某个电气量的 情况下,应选其作为参考相量。参考相量选定之后,即可由电路中参数的性质及其电压电流 的相位关系画出相量图。 8.复杂正弦交流电路的分析与计算 在复杂的 正弦交济 电路中,将电压和电流用相量表示之后,即可用支路电流法、回路 电流法、节电电压法、叠加原理、戴维南定理和诺顿定理等方法进行分析与计算。 9.谐振 在具有电感和电容元件的交流电路中,通过调节电路的参数或电源的频率而使电压与电 流同相,这时电路中就发生谐振现象(分为串联谐振和并联谐振)。 1)、串联谐振条件 X=X。或21=2可0 1 1 2)、串联诰振的特性 (1)电路的阻抗2=VR2+(X-Xc)2=R,其值最小。 在U不变得情况下,电流最大,1=1。=。· (2)=0(电源电压与电路中电流同相),电路对电源呈现电阻性。电源供给电路的 能量全部被电阻所消耗,电源与电路之间不发生能量的互换,能量的互换只发生在电感线圈 与电容器之间。 (3)ULHUc且在相位上相反,互相抵消,对整个电路不起作用,因此心=心R。 但么=优一名X及。=以。=受x的单维作用不容忽因为音X=X>R R 时,U1=Uc>U,电压过高可能会击穿线圈或电容器的绝缘)。串联谐振也称电压谐振。 电力工程中一般应避免之。 3、品质因数 Q=4=4」 1 元=t=a,CRR 称为电路的品质因数,简称Q值。其物理意义: (1)表示谐振时电感或电容上的电压是电源电压的Q倍: (2)值越大,则谐振曲线越尖锐,选择性越强。 4)、通频带宽度 在1=0,=方人,处颜率上下限之间的定度格为适颜带定度。即
3 电路)-并联谐振。 7. 在 R、L、C 电路中,如何选择参考相量 一般情况下,选公共量或已知量作为参考相量,比如在 R、L、C 串联电路中通常选电流 作为参考相量;在 R、L、C 并联电路中,通常选电压作为参考相量。但在已知某个电气量的 情况下,应选其作为参考相量。参考相量选定之后,即可由电路中参数的性质及其电压电流 的相位关系画出相量图。 8. 复杂正弦交流电路的分析与计算 在复杂的文正弦交流电路中,将电压和电流用相量表示之后,即可用支路电流法、回路 电流法、节电电压法、叠加原理、戴维南定理和诺顿定理等方法进行分析与计算。 9. 谐振 在具有电感和电容元件的交流电路中,通过调节电路的参数或电源的频率而使电压与电 流同相,这时电路中就发生谐振现象(分为串联谐振和并联谐振)。 1)、串联谐振条件 XL = X C 或 fC fL 2 1 2 = LC f 2 1 0 = , LC 1 = 0 = , arctan 0 L C = − = R X X 2)、串联谐振的特性 (1)电路的阻抗|Z|= 2 L C 2 R + (X − X ) = R ,其值最小。 在 U 不变得情况下,电流最大, I = I 0 = R U 。 (2) =0(电源电压与电路中电流同相),电路对电源呈现电阻性。电源供给电路的 能量全部被电阻所消耗,电源与电路之间不发生能量的互换,能量的互换只发生在电感线圈 与电容器之间。 (3)| L • U |=| C • U |且在相位上相反,互相抵消,对整个电路不起作用,因此 U U R • • = 。 但 L L X L R U U = IX = 及 C C X C R U U = IX = 的单独作用不容忽视(因为当 XL = X C R 时, UL = UC U ,电压过高可能会击穿线圈或电容器的绝缘)。串联谐振也称电压谐振。 电力工程中一般应避免之。 3)、品质因数 R L U CR U U U Q 0 0 C L 1 = = = = 称为电路的品质因数,简称 Q 值。其物理意义: (1)表示谐振时电感或电容上的电压是电源电压的 Q 倍; (2)值越大,则谐振曲线越尖锐,选择性越强。 4)、通频带宽度 在 0 0 2 1 I = 70.7%I = I 处频率上下限之间的宽度称为通频带宽度,即
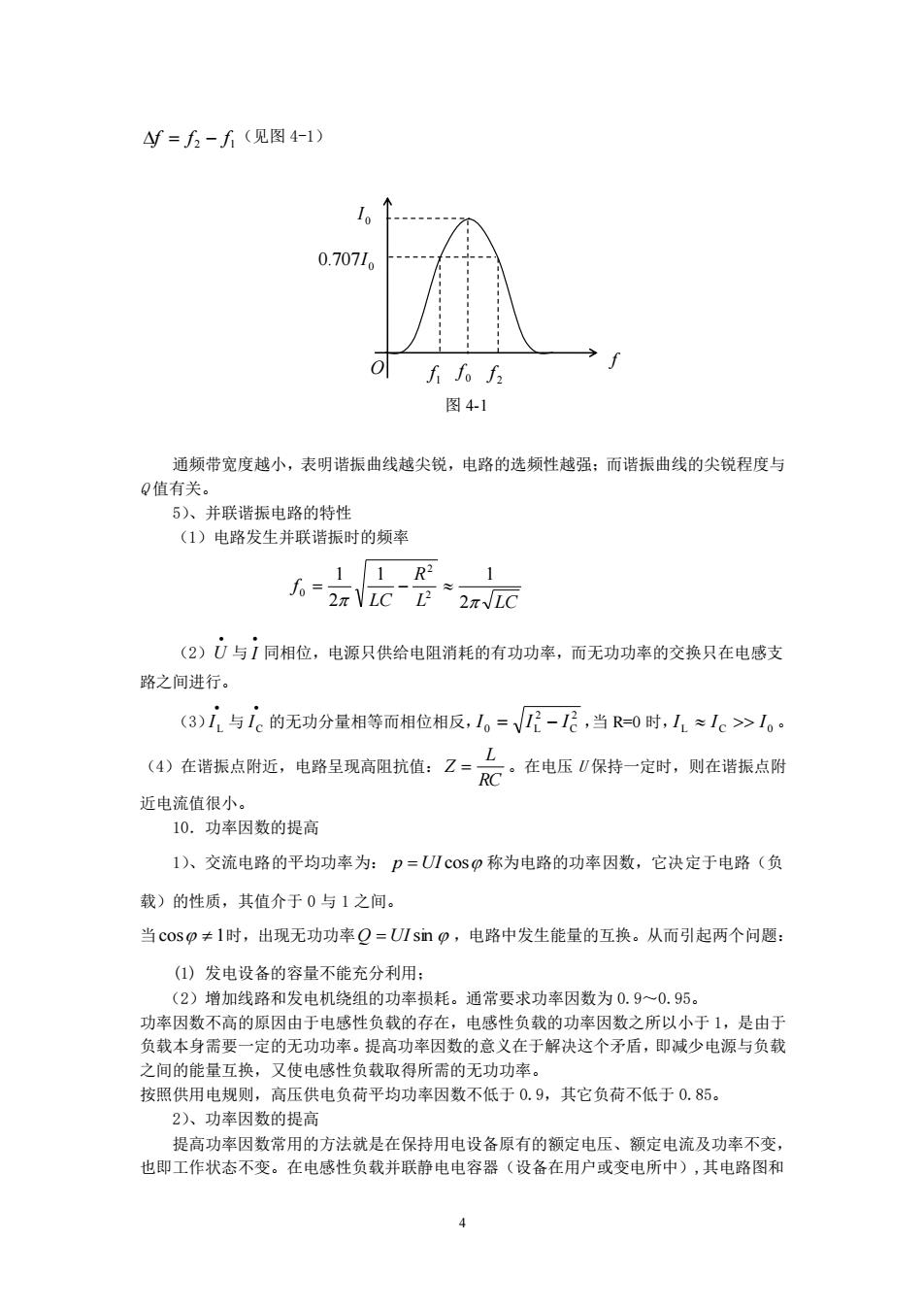
=5-斤(见图4-1) 0.7071 图4-1 通频带宽度越小,表明谐振曲线越尖锐,电路的选频性越强:而谐振曲线的尖锐程度与 Q值有关。 5)、并联诰振电路的特性 (1)电路发生并联谐振时的频率 6a限-是证 (2)U与1同相位,电源只供给电阻消耗的有功功率,而无功功率的交换只在电感支 路之间进行。 (3)1与1c的无功分量相等而相位相反,。=√-1?,当R=0时,11≈1c>1。· (④)在诺振点附近,电路呈现高阻抗值:乙=·在电压)保持一定时,则在谐振点附 近电流值很小。 10.功率因数的提高 1)、交流电路的平均功率为:p=U1cos称为电路的功率因数,它决定于电路(负 载)的性质,其值介于0与1之间。 当cosp≠1时,出现无功功率Q=UⅡsnp,电路中发生能量的互换。从而引起两个问题: (1)发电设备的容量不能充分利用: (2)增加线路和发电机绕组的功率损耗。通常要求功率因数为0.9~0.95。 功率因数不高的原因由于电感性负载的存在,电感性负载的功率因数之所以小于1,是由于 负载本身需要一定的无功功率。提高功率因数的意义在于解决这个矛盾,即减少电源与负较 之间的能量互换,又使电感性负载取得所需的无功功率。 按照供用电规则 高压供电负荷平均功率因数不低于0.9,其它负荷不低于0.85 2)、功率因数的提高 提高功奉因数常用的方法就是在保持用电设备原有的额定电压、额定电流及功率不变, 也即工作状态不变。在电感性负载并联静电电容器(设备在用户或变电所中),其电路图和 4
4 2 1 f = f − f (见图 4-1) 通频带宽度越小,表明谐振曲线越尖锐,电路的选频性越强;而谐振曲线的尖锐程度与 Q 值有关。 5)、并联谐振电路的特性 (1)电路发生并联谐振时的频率 L LC R LC f 2 1 1 2 1 2 2 0 = − (2) • U 与 • I 同相位,电源只供给电阻消耗的有功功率,而无功功率的交换只在电感支 路之间进行。 (3) • L I 与 • C I 的无功分量相等而相位相反, 2 C 2 0 L I = I − I ,当 R=0 时, L C 0 I I I 。 (4)在谐振点附近,电路呈现高阻抗值: RC L Z = 。在电压 U 保持一定时,则在谐振点附 近电流值很小。 10.功率因数的提高 1)、交流电路的平均功率为: p = UI cos 称为电路的功率因数,它决定于电路(负 载)的性质,其值介于 0 与 1 之间。 当 cos 1 时,出现无功功率 Q = UIsin ,电路中发生能量的互换。从而引起两个问题: (1) 发电设备的容量不能充分利用; (2)增加线路和发电机绕组的功率损耗。通常要求功率因数为 0.9~0.95。 功率因数不高的原因由于电感性负载的存在,电感性负载的功率因数之所以小于 1,是由于 负载本身需要一定的无功功率。提高功率因数的意义在于解决这个矛盾,即减少电源与负载 之间的能量互换,又使电感性负载取得所需的无功功率。 按照供用电规则,高压供电负荷平均功率因数不低于 0.9,其它负荷不低于 0.85。 2)、功率因数的提高 提高功率因数常用的方法就是在保持用电设备原有的额定电压、额定电流及功率不变, 也即工作状态不变。在电感性负载并联静电电容器(设备在用户或变电所中),其电路图和 f 1 f 0 f 2 f 707 0 0. I 0 I O 图 4-1

相量图如图4-2所示。 a) b) 图4-2 并联电容器以后,电感性负载的电流1,= R+X疗和功幸因数cos R+疗均未 R 变化,这是因为所加电压和负载参数没有改变。但电压和线路电流之间的相位差变小 了,即COs)变大了。这里所讲的提高功率因数,是指提高电源或电网的功率因数,而不是 指提高某个电感性负载的功率因数。因此,在选择静电电容器的容量时,必须了解补偿前同 载的平均功率因数,它可根据一年的电能消耗量来计算: P P 8760P 。 CO(87600+(8760P)W 式中P和Q分别是年消耗有功率(k)和无功功率(kva:W,和W。分别为年有功电能消 耗量(kW.h)和无功电能消耗量(kva·h),可由有功电度表和无功电度表读取:8760是 全年的总时数。 然后根据下式计算所需静电电容器的容量 O=(tan o -tan 式中Pm是负载的最大有功功率:y是负载系数,一般取0.85:是补偿前的相位差:p是 补偿后的相位差。或由相量图4-2b)推出该电容器的电容值 C=(tan-tan) 电容器的安装常采用高压集中补偿和低压分散补偿两种方式,也可以二者结合 P65练习与思考 4山有效位U=20V,了=30H%=-若 412p=9-02=60°=7 4.1.3
5 相量图如图 4-2 所示。 图 4-2 并联电容器以后,电感性负载的电流 2 L 2 1 1 R X I + = 和功率因数 2 L 2 1 cos R X R + = 均未 变化,这是因为所加电压和负载参数没有改变。但电压 U 和线路电流 i 之间的相位差 变小 了,即 cos 变大了。这里所讲的提高功率因数,是指提高电源或电网的功率因数,而不是 指提高某个电感性负载的功率因数。因此,在选择静电电容器的容量时,必须了解补偿前同 载的平均功率因数,它可根据一年的电能消耗量来计算: 2 Q 2 P P 2 2 2 2 1 (8760 ) (8760 ) 8760 cos W W W Q P P Q P P S P + = + = + = = 式中 P 和 Q 分别是年消耗有功率(kW)和无功功率(kvar); WP 和 WQ 分别为年有功电能消 耗量 (kW h) 和无功电能消耗量( k var h ),可由有功电度表和无功电度表读取;8760 是 全年的总时数。 然后根据下式计算所需静电电容器的容量 (tan tan ) Q = Pmax 1 − 式中 Pmax 是负载的最大有功功率; 是负载系数,一般取 0.85; 1 是补偿前的相位差; 是 补偿后的相位差。或由相量图 4-2b)推出该电容器的电容值 (tan tan ) 2 1 2 = − U p C 电容器的安装常采用高压集中补偿和低压分散补偿两种方式,也可以二者结合。 P65 练习与思考 4.1.1 有效值 U = 220V, = 50HZ f , 6 0 = − 4.1.2 3 600 1 2 = − = = 4.1.3