第十章 无穷级数 一、知识结构图与学习要求 (一)知识结构图 基本概念 收敛级数的基本性质 「利用定义(部分和 常数项级数 比较审敛法(包括极限形式) (正项级数 比值审敛法 审敛法 、根值审敛法 交错级数:莱布尼茨定理 无穷 一般项级数:绝对收敛与条件收敛 基本概 收敛半径与收敛域 幂级数 和函数(并由此求某些常数项级数的和) 函数项级数 ,将函数展开成幂级数(泰勒级数) 基本概念 收敛性的判定:收敛定理(狄利克雷充分条件)》 傅里叶级数 (在对称区间-1,刀上展开 展开为傅里叶级数〈在区间0,)上展开 展开为正弦或余弦级数 (二)学习要求 1,理解常数项级数收敛、发散以及收敛级数的和的概念,掌握级数的基本性质及收敛 的必要条件
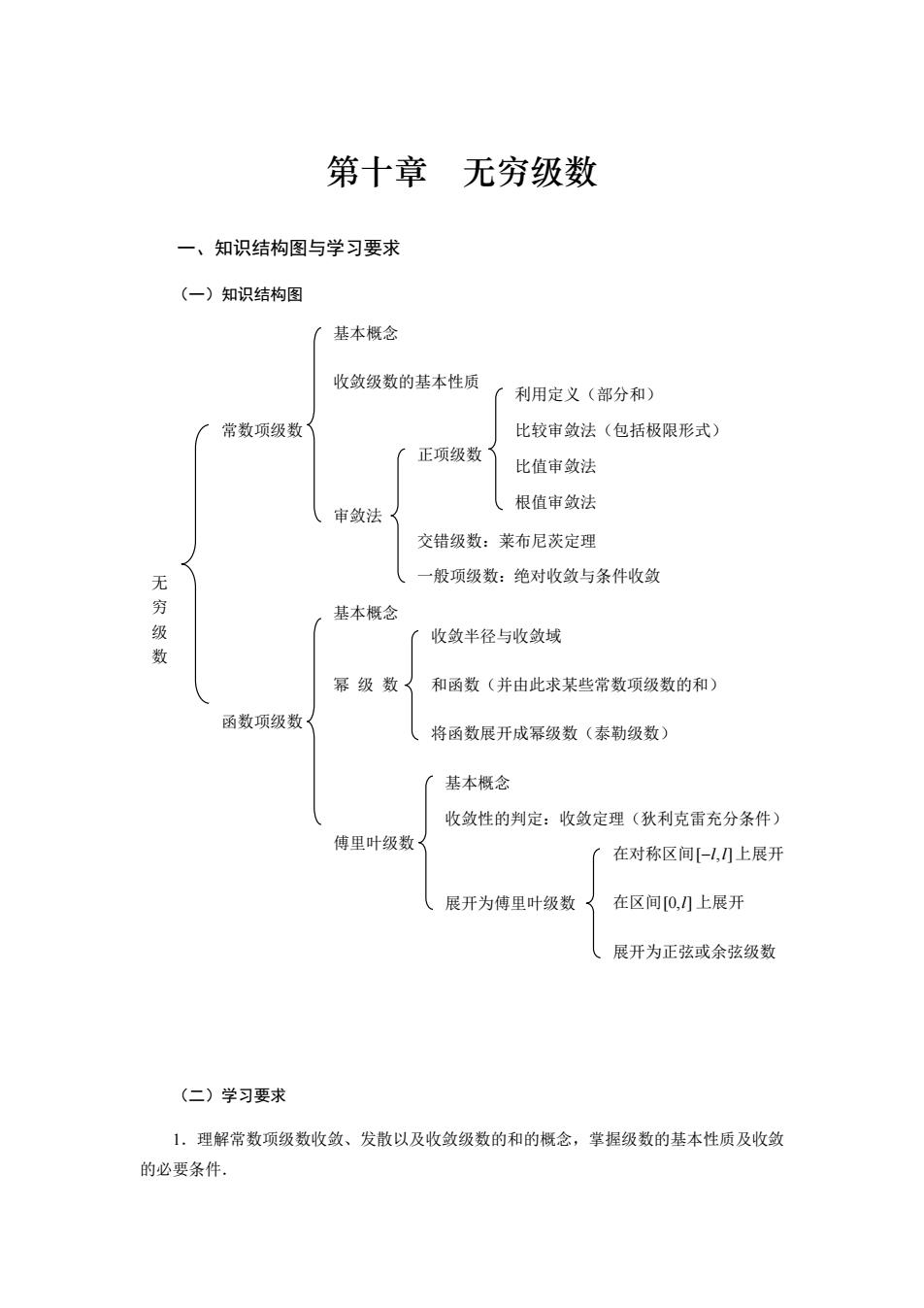
第十章 无穷级数 一、知识结构图与学习要求 (一)知识结构图 (二)学习要求 1.理解常数项级数收敛、发散以及收敛级数的和的概念,掌握级数的基本性质及收敛 的必要条件. 无 穷 级 数 常数项级数 函数项级数 傅里叶级数 基本概念 审敛法 收敛级数的基本性质 一般项级数:绝对收敛与条件收敛 正项级数 比较审敛法(包括极限形式) 展开为正弦或余弦级数 比值审敛法 利用定义(部分和) 基本概念 幂 级 数 交错级数:莱布尼茨定理 根值审敛法 基本概念 收敛性的判定:收敛定理(狄利克雷充分条件) 展开为傅里叶级数 将函数展开成幂级数(泰勒级数) 和函数(并由此求某些常数项级数的和) 收敛半径与收敛域 在对称区间 [ , ] −l l 上展开 在区间 [0, ]l 上展开

2.掌握几何级数与p-级数的收敛与发散的条件。 3.掌正项级数收敛性的比较审敛法和比值市敛法,会用根值市敛法。 4.掌握交错级数的菜布尼茨审敛法。 5.了解任意项级数绝对收敛与条件收敛的概念,以及绝对收敛与条件收敛的关系。 6.了解函数项级数的收敛域及和函数的概念. 7.理解幂级数的收敛半径的概念、掌握幂级数的收敛半径、收敛区间及收敛域的求 法 8.了解幂级数在其收敛区间内的一些基本性质(和函数的连续性、逐项求导和逐项 积分),会求一些幂级数在收敛区间内的和函数,并会由此求出某些常数项级数的和. 9.了解函数展开为泰勒级数的充分必要条件. 10.掌握e、sinx、cosx、nl+x)和(1+x的麦克劳林展开式,会用它们将一些简 单函数间接展开成幂级数 11.了解傅里叶级数的概念和狄利克雷收敛定理,会将定义在[-1,】上的函数展开为傅 里叶级数,会将定义在[0,】上的函数展开为正弦级数与余弦级数,会写出傅里叶级数的和 的表达式 二、内容提要 (一)常数项级数 1.概念 ()若级数立,的部分和数列=4+%++)有极限s,即m5=5,则称 无穷级数∑山,收敛,并称s为它的和,记为5=∑4:否则称它是发散的。 (2)称级数∑u,(似,≥0,n=12)为正项级数.称级数∑(-)一u,或∑(-°4,(其中 4。>0)为交错级数 (3)如果级数立以,收敛,则称级数∑“,绝对收敛:如果级数立山,发散,而级数三 收敛,则称级数∑”,条件收敛 2.定理(性质) (1)几何级数 g=1+g+g++g+
2.掌握几何级数与 p − 级数的收敛与发散的条件. 3.掌握正项级数收敛性的比较审敛法和比值审敛法,会用根值审敛法. 4.掌握交错级数的莱布尼茨审敛法. 5.了解任意项级数绝对收敛与条件收敛的概念,以及绝对收敛与条件收敛的关系. 6.了解函数项级数的收敛域及和函数的概念. 7.理解幂级数的收敛半径的概念、掌握幂级数的收敛半径、收敛区间及收敛域的求 法. 8.了解幂级数在其收敛区间内的一些基本性质(和函数的连续性、逐项求导和逐项 积分),会求一些幂级数在收敛区间内的和函数,并会由此求出某些常数项级数的和. 9.了解函数展开为泰勒级数的充分必要条件. 10.掌握 x e 、sin x 、 cos x 、 ln(1 ) + x 和 (1 )x + 的麦克劳林展开式,会用它们将一些简 单函数间接展开成幂级数. 11.了解傅里叶级数的概念和狄利克雷收敛定理,会将定义在 [ , ] −l l 上的函数展开为傅 里叶级数,会将定义在 [0, ]l 上的函数展开为正弦级数与余弦级数,会写出傅里叶级数的和 的表达式. 二、内容提要 (一)常数项级数 1.概念 (1)若级数 1 n n u = 的部分和数列 1 2 ( ) n n n s s u u u = + + + 有极限 s ,即 lim n n s s → = ,则称 无穷级数 1 n n u = 收敛,并称 s 为它的和,记为 1 n n s u = = ;否则称它是发散的. (2)称级数 1 ( 0, 1,2, ) n n n u u n = = 为正项级数.称级数 1 1 ( 1)n n n u − = − 或 1 ( 1)n n n u = − (其中 0 n u )为交错级数. (3)如果级数 1 n n u = 收敛,则称级数 1 n n u = 绝对收敛;如果级数 1 n n u = 发散,而级数 1 n n u = 收敛,则称级数 1 n n u = 条件收敛. 2.定理(性质) (1)几何级数 2 0 1 n n n q q q q = = + + + + +

当<1时收敛。其和为一g而当21时发散。 (2)p-级数 品=1宁可宁.p是常数. 当p>1时收敛:而当p≤1时发散.特别地,当p=1时,调和级数 =1+分++.++. 发散 3)设级数三,和立,都收敛,则级数立以,士,)收敛,由此可知 a.若∑“,收敛,∑发散,则∑,±,)发散: b.若立.发散,工,发散,则正化,±)收敛性不定: 。若立4,与,均绝对收敛,则u,士)绝对收敛: d.若∑”绝对收敛,∑.条件收敛,则∑(以,±,)条件收敛. (4)设级数∑4.收敛,k为一个常数,则 a.∑k,收敛且im私.=0.(若m,≠0,则级数∑4,发散.) b.对∑,中的项任意加括号后所得的新级数仍收敛。(如果对级数∑,的项加括号后 所得新级数发散,则原级数发散.) (5)在级数中去掉、加上或改变有限项,不会改变级数的收敛性。 (6)如果级数∑“,绝对收敛,则级数∑4,必定收敛. 3.方法 (1)正项级数的审敛法: a.利用级数收敛的定义: b.利用级数收敛的充要条件:级数收敛一部分和数列有界: c.比较审敛法: d.比值审敛法: e.根值审敛法: £.极限审敛法。 (2)交错级数的市敛法:莱布尼茨定理. (3)一般项级数∑“,的审敛法:先转换为判别是否是收敛,若收敛,则原级数
当 q 1 时收敛,其和为 1 1− q ,而当 q 1 时发散. (2) p − 级数 1 1 1 1 1 1 2 3 p p p p n n n = = + + + + + ( p 是常数), 当 p 1 时收敛;而当 p 1 时发散.特别地,当 p =1 时,调和级数 1 1 1 1 1 1 n n n 2 3 = = + + + + + 发散. (3)设级数 1 n n u = 和 1 n n v = 都收敛,则级数 1 ( ) n n n u v = 收敛.由此可知: a.若 1 n n u = 收敛, 1 n n v = 发散,则 1 ( ) n n n u v = 发散; b.若 1 n n u = 发散, 1 n n v = 发散,则 1 ( ) n n n u v = 收敛性不定; c.若 1 n n u = 与 1 n n v = 均绝对收敛,则 1 ( ) n n n u v = 绝对收敛; d.若 1 n n u = 绝对收敛, 1 n n v = 条件收敛,则 1 ( ) n n n u v = 条件收敛. (4)设级数 1 n n u = 收敛, k 为一个常数,则 a. 1 n n ku = 收敛且 lim 0 n n u → = .(若 lim 0 n n u → ,则级数 1 n n u = 发散.) b.对 1 n n u = 中的项任意加括号后所得的新级数仍收敛.(如果对级数 1 n n u = 的项加括号后 所得新级数发散,则原级数发散.) (5)在级数中去掉、加上或改变有限项,不会改变级数的收敛性. (6)如果级数 1 n n u = 绝对收敛,则级数 1 n n u = 必定收敛. 3.方法 (1)正项级数的审敛法: a.利用级数收敛的定义; b.利用级数收敛的充要条件:级数收敛 部分和数列有界; c.比较审敛法; d.比值审敛法; e.根值审敛法; f.极限审敛法. (2)交错级数的审敛法:莱布尼茨定理. (3)一般项级数 1 n n u = 的审敛法:先转换为判别 1 n n u = 是否是收敛,若收敛,则原级数

绝对收敛,然后判别是条件收敛还是发散。 (二)函数项级数(主要讨论幂级数) 1.概念 (1)由定义在区间1上的函数列{u.(x所构成的表达式: 4(x)+,(x)+.+,(x)+. 称为定义在区间1的函数项级数,记为∑”,(x) (2)对于某个∈1,如果∑4,(G)收敛,则称是函数项级数∑“,(国的收敛点, 收敛点的全体称为∑“,)的收敛域:如果工“(化)发散,则称x是函数项级数立()的 发散点,发散点的全体称为三,()的发散域 (3)在收敛域/上,函数项级数∑“,(x)的和是x的函数,记为s(x),称sx)为函数项 级数∑4,(x)的和函数,即有 s)=∑4(x)=4(x)+4(x)+.+,(x)+,xe1. (4)5()=4(x)+,(x)++.()称为函数项级数∑,x)的部分和,则在收敛域上 有ms,()=s,称)=)-)为函数项级数()的余项 (5)形如 三ar=ata+af++ar+ 的函数项级数称为x的幂级数,而形如 2a,x-广=a+ax-+a-++a-6+. 的幂级数称为(x-)的幂级数,其中a(n=0,l2,)称为幂级数的系数。 (6)如果幂级数,”不是仅在x=0一点收敛,也不是在整个实数轴上都收敛,则 必有唯一确定的正数R存在,使得当<R时,幂级数∑·绝对收敛,当内>R时,幂 级数Q,r发散,当x=R与x=-R时,幂级数,r可能收敛也可能发散.此时称正数R 为幂级数∑a,x的收敛半径.如果幂级数∑a仅在x=0处收敛,则它的收敛半径R=0:
绝对收敛,然后判别是条件收敛还是发散. (二)函数项级数(主要讨论幂级数) 1.概念 (1)由定义在区间 I 上的函数列 u x n ( ) 所构成的表达式: 1 2 ( ) ( ) ( ) n u x u x u x + + + + 称为定义在区间 I 的函数项级数,记为 1 ( ) n n u x = . (2)对于某个 0 x I ,如果 0 1 ( ) n n u x = 收敛,则称 0 x 是函数项级数 1 ( ) n n u x = 的收敛点, 收敛点的全体称为 1 ( ) n n u x = 的收敛域;如果 0 1 ( ) n n u x = 发散,则称 0 x 是函数项级数 1 ( ) n n u x = 的 发散点,发散点的全体称为 1 ( ) n n u x = 的发散域. (3)在收敛域 I 上,函数项级数 1 ( ) n n u x = 的和是 x 的函数,记为 sx( ) ,称 sx( ) 为函数项 级数 1 ( ) n n u x = 的和函数,即有 sx( ) = 1 ( ) n n u x = = 1 2 ( ) ( ) ( ) n u x u x u x + + + + , x I . (4) 1 2 ( ) ( ) ( ) ) ( n n s x = u x u x u + + + x 称为函数项级数 1 ( ) n n u x = 的部分和,则在收敛域上 有 lim ( ) ( ) n n s x s x → = ,称 ( ) ( ) ( ) n n r x s x s x = − 为函数项级数 1 ( ) n n u x = 的余项. (5)形如 2 0 1 2 0 n n n n n a x a a x a x a x = = + + + + + 的函数项级数称为 x 的幂级数,而形如 2 0 0 1 0 2 0 0 0 ( ) ( ) ( ) ( ) n n n n n a x x a a x x a x x a x x = − = + − + − + + − + 的幂级数称为 0 ( ) x x − 的幂级数,其中 ( 0,1,2, ) n a n = 称为幂级数的系数. (`6)如果幂级数 0 n n n a x = 不是仅在 x = 0 一点收敛,也不是在整个实数轴上都收敛,则 必有唯一确定的正数 R 存在,使得当 x R 时,幂级数 0 n n n a x = 绝对收敛,当 x R 时,幂 级数 0 n n n a x = 发散,当 x R = 与 x R =− 时,幂级数 0 n n n a x = 可能收敛也可能发散.此时称正数 R 为幂级数 0 n n n a x = 的收敛半径.如果幂级数 0 n n n a x = 仅在 x = 0 处收敛,则它的收敛半径 R = 0;

如果幕级数∑a,在整个实数轴上收敛,则它的收敛半径R=+0。 开区间(一R风)称为幂级数∑a,”的收敛区间,而幂级数∑a,r的收敛域是(一R,R) (R风,【R)及-R风其中之一 (7)如果函数f(x)在点,的某邻域内具有各阶导数f(x),(x),(x),则 (x-)的幂级数 n-xr一2g-r 称为函数∫x)的泰物级数.特别取x,=0,则级数变为 称此级数为麦克劳林级数 2.定理(性质) (1)AbeI定理 如果幂级数∑a,x当x=x(≠0)时收敛,则适合不等式<k的一切x使这幂级数 绝对收敛:反之,如果幂级数∑a,x当x=x,时发散,则适合不等式>的一切x使这 幂级数发散。 @)设级故字0,知果回p,其中a、是蒂级数空a的相每两顶 的系数,则该幂级数的收敛半径 1 R= D P*0 +,p=0 0,p= 注定理中条件回侣仅仅是求幂级数收敛半径的充分条件,而非必要条件。 (3)幂级数∑a,x的和函数s)在其收敛域1上连续 (4)幂级数工4,的和函数s()在其收敛域/上可积,并有逐项积分公式 st-吃a,r-2a,r=2+r,xeD
如果幂级数 0 n n n a x = 在整个实数轴上收敛,则它的收敛半径 R = + . 开区间 ( , ) −R R 称为幂级数 0 n n n a x = 的收敛区间,而幂级数 0 n n n a x = 的收敛域是 ( , ) −R R , ( , ] −R R ,[ , ) −R R 及 [ , ] −R R 其中之一. (7)如果函数 f x( ) 在点 0 x 的某邻域内具有各阶导数 ( ) ( ), ( ), , ( ), n f x f x f x ,则 0 ( ) x x − 的幂级数 ( ) 0 0 2 0 0 0 0 0 ( ) ( ) ( ) ( )( ) ( ) ( ) 2! ! n n f x f x f x f x x x x x x x n + − + − + + − + = ( ) 0 0 0 ( ) ( ) ! n n n f x x x n = − 称为函数 f x( ) 的泰勒级数.特别取 0 x = 0,则级数变为 ( ) ( ) 2 0 (0) (0) (0) (0) (0) 2! ! ! n n n n n f f f f f x x x x n n = + + + + + = , 称此级数为麦克劳林级数. 2.定理(性质) (1) Abel 定理 如果幂级数 0 n n n a x = 当 0 0 x x x = ( 0) 时收敛,则适合不等式 0 x x 的一切 x 使这幂级数 绝对收敛;反之,如果幂级数 0 n n n a x = 当 0 x x = 时发散,则适合不等式 0 x x 的一切 x 使这 幂级数发散. (2)设幂级数 0 n n n a x = ,如果 1 lim n n n a a + → = ,其中 n a 、 n 1 a + 是幂级数 0 n n n a x = 的相邻两项 的系数,则该幂级数的收敛半径 1 , 0 , 0 0 , R = + = = + . 注 定理中条件 1 lim n n n a a + → = 仅仅是求幂级数收敛半径的充分条件,而非必要条件. (3)幂级数 0 n n n a x = 的和函数 sx( ) 在其收敛域 I 上连续. (4)幂级数 0 n n n a x = 的和函数 sx( ) 在其收敛域 I 上可积,并有逐项积分公式 0 ( ) x s x dx = 0 [ ] x n n o n a x dx = = 0 0 x n n n a x dx = = 1 0 1 n n n a x n + = + ,( ) x I .