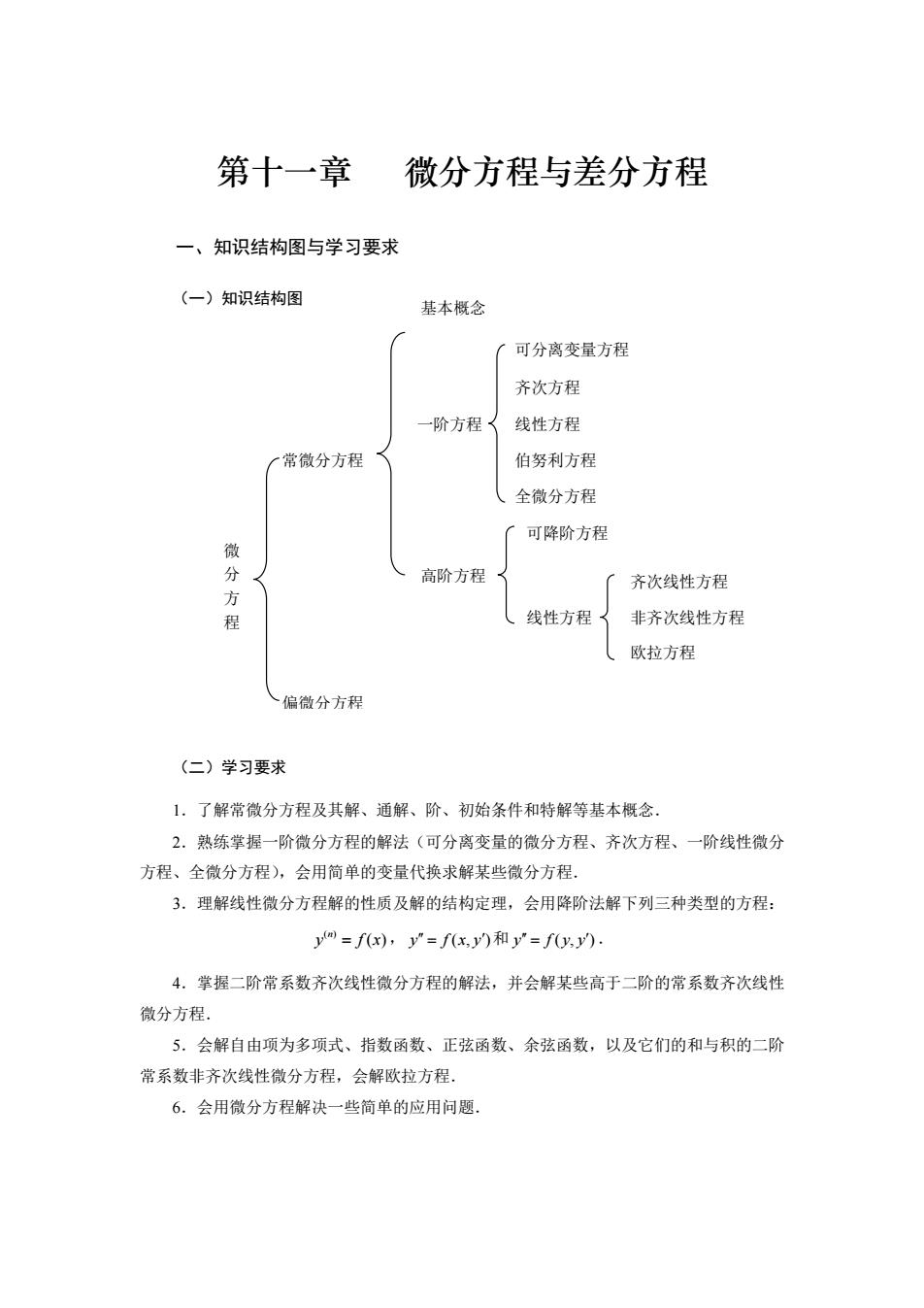
第十一章 微分方程与差分方程 一、知识结构图与学习要求 (一)知识结构图 基本概念 可分离变量方程 齐次方程 一阶方程 线性方程 常微分方程 伯努利方程 、全微分方程 可降阶方程 高阶方程 齐次线性方程 线性方程 非齐次线性方程 欧拉方程 偏微分方程 (二)学习要求 1.了解常微分方程及其解、通解、阶、初始条件和特解等基本概念. 2.熟练掌握一阶微分方程的解法(可分离变量的微分方程、齐次方程、一阶线性微分 方程、全微分方程),会用简单的变量代换求解某些微分方程. 3.理解线性微分方程解的性质及解的结构定理,会用降阶法解下列三种类型的方程: y=fx),y=fx,和y'=fy 4.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性 微分方程. 5.会解自由项为多项式、指数函数、正弦函数、余弦函数,以及它们的和与积的二阶 常系数非齐次线性微分方程,会解欧拉方程。 6.会用微分方程解决一些简单的应用问题
第十一章 微分方程与差分方程 一、知识结构图与学习要求 (一)知识结构图 (二)学习要求 1.了解常微分方程及其解、通解、阶、初始条件和特解等基本概念. 2.熟练掌握一阶微分方程的解法(可分离变量的微分方程、齐次方程、一阶线性微分 方程、全微分方程),会用简单的变量代换求解某些微分方程. 3.理解线性微分方程解的性质及解的结构定理,会用降阶法解下列三种类型的方程: ( ) ( ) n y f x = , y f x y = ( , ) 和 y f y y = ( , ) . 4.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性 微分方程. 5.会解自由项为多项式、指数函数、正弦函数、余弦函数,以及它们的和与积的二阶 常系数非齐次线性微分方程,会解欧拉方程. 6.会用微分方程解决一些简单的应用问题. 微 分 方 程 偏微分方程 可分离变量方程 线性方程 常微分方程 高阶方程 伯努利方程 一阶方程 齐次方程 齐次线性方程 可降阶方程 线性方程 欧拉方程 非齐次线性方程 全微分方程 基本概念

二、内容提要 (一)微分方程的基本概念 1.凡表示未知函数、未知函数的导数与自变量之间的关系的方程,叫做微分方程。未 知函数是一元函数的,叫做常微分方程.未知函数是多元函数的,叫做偏微分方程 2.微分方程中所出现的未知函数的最高阶导数的阶数,叫做微分方程的阶 3.如果一个函数代入微分方程能使该方程成为恒等式,则称这个函数为微分方程的 解.如果微分方程的解中所含的独立的任意常数的个数与方程的阶数相同,那么此解称为微 分方程的通解。确定了通解中的任意常数以后,就得到微分方程的特解。 4.求微分方程y=fx,)满足初始条件yL,=%的特解,叫做一阶微分方程的初值问 题,记作 [y=f(x.y) y儿=% 微分方程的解的图形是一条曲线,叫做微分方程的积分曲线,以上初值问题的几何意义就是 求微分方程的通过定点(化%)的积分曲线。 (二)一阶方程 1.可分离变量的微分方程 一般地,如果一个一阶微分方程能写成gy)=(x)的形式,那么原方程就称为可 分离变量的微分方程,这类方程只需要在g=fx)达两边同时积分即可求解。这是微 分方程中最基本的类型, 2.齐次方程 如果一阶微分方程虫=:)中的函数x,)可写成兰的函数,即f化列=白,则 d 称该方程为齐次方程. 求解齐次方程,通常作变换山=二,即y=心,并对其两端关于x求导得 代入隙方程,原方程即可化为可分离变量方程,求出此可分离变量方程的通解后,以上代 替“,即可得到原方程的通解。 3.一阶线性微分方程 (I)形如少+P(xy=Q(x)的方程叫做一阶线性微分方程 dx a.如果(x)=0,则该方程称为齐次的,此时方程属于可分离变量的微分方程,求解
二、内容提要 (一)微分方程的基本概念 1.凡表示未知函数、未知函数的导数与自变量之间的关系的方程,叫做微分方程.未 知函数是一元函数的,叫做常微分方程.未知函数是多元函数的,叫做偏微分方程. 2.微分方程中所出现的未知函数的最高阶导数的阶数,叫做微分方程的阶. 3.如果一个函数代入微分方程能使该方程成为恒等式,则称这个函数为微分方程的 解.如果微分方程的解中所含的独立的任意常数的个数与方程的阶数相同,那么此解称为微 分方程的通解.确定了通解中的任意常数以后,就得到微分方程的特解. 4.求微分方程 y f x y = ( , ) 满足初始条件 0 0 | x x y y = = 的特解,叫做一阶微分方程的初值问 题,记作 0 0 ( , ) | x x y f x y y y = = = , 微分方程的解的图形是一条曲线,叫做微分方程的积分曲线,以上初值问题的几何意义就是 求微分方程的通过定点 0 0 ( , ) x y 的积分曲线. (二)一阶方程 1.可分离变量的微分方程 一般地,如果一个一阶微分方程能写成 g y dy f x dx ( ) ( ) = 的形式,那么原方程就称为可 分离变量的微分方程,这类方程只需要在 g y dy f x dx ( ) ( ) = 两边同时积分即可求解.这是微 分方程中最基本的类型. 2.齐次方程 如果一阶微分方程 ( , ) dy f x y dx = 中的函数 f x y ( , ) 可写成 y x 的函数,即 ( , ) ( ) y f x y x = ,则 称该方程为齐次方程. 求解齐次方程,通常作变换 y u x = ,即 y ux = ,并对其两端关于 x 求导得 dy du u x dx dx = + , 代入原方程,原方程即可化为可分离变量方程,求出此可分离变量方程的通解后,以 y x 代 替 u ,即可得到原方程的通解. 3.一阶线性微分方程 (1)形如 ( ) ( ) dy P x y Q x dx + = 的方程叫做一阶线性微分方程. a.如果 Q x( ) 0 ,则该方程称为齐次的,此时方程属于可分离变量的微分方程,求解

得y=Ce咖(此处用Pr太表示Px)的某个确定的原函数): b.如果(x)不恒等于零,则该方程称为非齐次的,利用常数变易法可求该非齐次线性 方程的通解。用常数变易法求女+P(沙=Q)通解的一般步骤如下: 第一步,求出会+Pey=0的通解y=C, 第二步:变易常数,即令y=Cxea是虫+Py=C)的解 第三步:将y=Ceh代入办+P=Q,求出 Co)=foure+c: 第四步:将C)=「Q(xe本+C代入y=C(xePa恤中即可得到一阶线性非齐次方 程密+P代wy=Q)的通解为 y=era恤((xex+C. 约定本章中出现的C,如果未加说明均指任意常数. (2)形如央+P=Qxy(a≠0)的方程称为伯努利((Bernou1li)方程,当n=0 或1时,方程是线性微分方程. 伯努利方程的求解:令:=)一得安=1-小少一会,原方程即可化为一阶线性方程 表+0-nr=-nQ 求出该方程的通解,再将:=y代入即得到该伯努利方程的通解。 4.全微分方程 (1)若一阶微分方程P(x,)达+(x,y)=0的左端恰好是某一个函数u=4(x,)的全 微分,即dx,y)=Px,y体+Q(x,y,则该方程叫做全微分方程.因此,x)=C是全 微分方程的隐式通解。 (2)当P(x,y),Qx,y)在单连通域G内具有一阶连续偏导数时,则方程 P(x.y)dx+(x.y)dy=0 为全微分方程的无要条件是器一器在区线G内恒成立 (3)求全微分方程的通解有如下三种常用方法, 方法1利用方程P(x,y)d+Q(x,y)d=0在单连通域G内是全微分方程的充要条件是 架-器。即自线积分达+冰在率连道城G内与积分路径无关,得
得 P x dx ( ) y Ce− = (此处用 P x dx ( ) 表示 P x( ) 的某个确定的原函数); b.如果 Q x( ) 不恒等于零,则该方程称为非齐次的,利用常数变易法可求该非齐次线性 方程的通解.用常数变易法求 ( ) ( ) dy P x y Q x dx + = 通解的一般步骤如下: 第一步:求出 ( ) 0 dy P x y dx + = 的通解 P x dx ( ) y Ce− = ; 第二步:变易常数,即令 ( ) ( ) P x dx y C x e− = 是 ( ) ( ) dy P x y Q x dx + = 的解; 第三步:将 ( ) ( ) P x dx y C x e− = 代入 ( ) ( ) dy P x y Q x dx + = ,求出 ( ) ( ) ( ) P x dx C x Q x e dx C = + ; 第四步:将 ( ) ( ) ( ) P x dx C x Q x e dx C = + 代入 ( ) ( ) P x dx y C x e− = 中即可得到一阶线性非齐次方 程 ( ) ( ) dy P x y Q x dx + = 的通解为 ( ) ( ) ( ( ) ) P x dx P x dx y e Q x e dx C − = + . 约定 本章中出现的 C ,如果未加说明均指任意常数. (2)形如 ( ) ( ) ( 0,1) dy n P x y Q x y n dx + = 的方程称为伯努利(Bernoulli)方程,当 n = 0 或 1 时,方程是线性微分方程. 伯努利方程的求解:令 1 n z y − = 得 (1 ) dz dy n n y dx dx − = − ,原方程即可化为一阶线性方程 (1 ) ( ) (1 ) ( ) dz n P x z n Q x dx + − = − , 求出该方程的通解,再将 1 n z y − = 代入即得到该伯努利方程的通解. 4.全微分方程 (1)若一阶微分方程 P x y dx Q x y dy ( , ) ( , ) 0 + = 的左端恰好是某一个函数 u u x y = ( , ) 的全 微分,即 du x y P x y dx Q x y dy ( , ) ( , ) ( , ) = + ,则该方程叫做全微分方程.因此, u x y C ( , ) = 是全 微分方程的隐式通解. (2)当 P x y ( , ),Q x y ( , ) 在单连通域 G 内具有一阶连续偏导数时,则方程 P x y dx Q x y dy ( , ) ( , ) 0 + = 为全微分方程的充要条件是 P Q y x = 在区域 G 内恒成立. (3)求全微分方程的通解有如下三种常用方法. 方法 1 利用方程 P x y dx Q x y dy ( , ) ( , ) 0 + = 在单连通域 G 内是全微分方程的充要条件是 P Q y x = ,即曲线积分 ( , ) ( , ) L P x y dx Q x y dy + 在单连通域 G 内与积分路径无关,得

ux,y)=∫”Pk+Q=Px,d+∫广x,y 或者 xy=∫广Qy冰+∫广Px 其中(,%)为G内任一定点. 方法2设dM=Px,y冰+Qx,y,则 .)u) x y 在”-列两边积分得 ux,y)=P(x.y)d+y), 而由,》=Qx,列可得 =》k+p0, dy 由此式解出'),积分得0).从而求出函数(x,y), 同理,也可以先由M》=Qx列求得 y x,y)=∫x,yd+() 再由x2=Px,)和上式得 PW-=∫”+o: 解出D(x),积分求得(x),从而可求出函数(x,y). 方法3把P(x,y)+Qx,y冲=0左边凑微分凑成Px,y)本+Qx,y)d=d,则 x,)=C即为所求的通解 (4)当方程P(x,yd+Qx,y=0不是全微分方程,这时如果存在一个适当的函数 4=(x)(4x,)≠0)使4(x,)P(x,)+x,yOx,y)d=0是全微分方程,则称函数 (x,)为该方程的积分因子.求积分因子一般此较困难,积分因子如果存在则不唯一,因 而通解可能具有不同的形式. 常见的一些凑微分公式 xdy+ydx=d(xy), xdx+ydy=d(x+y), -达=白
0 0 0 0 ( , ) 0 ( , ) ( , ) ( , ) ( , ) x y x y x y x y u x y Pdx Qdy P x y dx Q x y dy = + = + 或者 u x y ( , ) 0 0 0 ( , ) ( , ) y x y x = + Q x y dy P x y dy , 其中 0 0 ( , ) x y 为 G 内任一定点. 方法 2 设 du P x y dx Q x y dy = + ( , ) ( , ) ,则 ( , ) ( , ) u x y P x y x = , ( , ) ( , ) u x y Q x y y = , 在 ( , ) ( , ) u x y P x y x = 两边积分,得 u x y P x y dx y ( , ) ( , ) ( ) = + , 而由 ( , ) ( , ) u x y Q x y y = 可得 ( , ) ( , ) [ ( , ) ( )] u x y Q x y P x y dx y y y = = + ( , ) ( ) P x y dx y y = + , 由此式解出 ( ) y ,积分得 ( ) y .从而求出函数 u x y ( , ) . 同理,也可以先由 ( , ) ( , ) u x y Q x y y = 求得 u x y Q x y dy x ( , ) ( , ) ( ) = + , 再由 ( , ) ( , ) u x y P x y x = 和上式得 ( , ) ( , ) ( ) Q x y P x y dy x x = + , 解出 ( ) x ,积分求得 ( ) x ,从而可求出函数 u x y ( , ) . 方法 3 把 P x y dx Q x y dy ( , ) ( , ) 0 + = 左边凑微分凑成 P x y dx Q x y dy du ( , ) ( , ) + = ,则 u x y C ( , ) = 即为所求的通解. (4)当方程 P x y dx Q x y dy ( , ) ( , ) 0 + = 不是全微分方程,这时如果存在一个适当的函数 = ( , ) ( ( , ) 0) x y x y 使 ( , ) ( , ) ( , ) ( , ) 0 x y P x y dx x y Q x y dy + = 是全微分方程,则称函数 ( , ) x y 为该方程的积分因子.求积分因子一般比较困难,积分因子如果存在则不唯一, 因 而通解可能具有不同的形式. 常见的一些凑微分公式 xdy ydx d xy + = ( ), 1 2 2 ( ) 2 xdx ydy d x y + = + , 2 2 2 2 1 ln( ) 2 xdx ydy d x y x y + = + + , 2 ( ) xdy ydx y d x x − =

二地=, :*-m3 - r-V -达=dn宁, 2-广达= r 29-边=a月 y (三)可降阶的高阶微分方程 下面介绍三种容易降阶的高阶微分方程的求解方法. 1.=fx)型的微分方程 对此方程两边连续积分”次,每积分一次增加一个任意常数,便得此方程的含有n个任 意常数的通解. 2.y=fx,y型的微分方程 此方程的特点是方程中不显含,设y=P:则有)广=安=p,那么原方程转化为一 阶方程p=fx,P),这是关于x、p的一阶微分方程,求出其通解p=(x,C),即得到另 一个一阶方程y=(x,C),两边积分即可得到原方程的通解为y=∫(x,C+C,其中C, C,是任意常数. 3.y=fy,y型的微分方程 此方程的特点是方程中不显含自变量x,令y=P,则有 密等盘喘 原方程转化为P尖=心P小,这是关于变量)小、P的一阶微分方程,设求出的通解为 y=P=y,C),此方程为变量可分离的方程,分离变量然后积分即可得到原方程的通解为 高。+G,共中G、G是任意落数 (四)高阶线性微分方程 1.线性微分方程的解的结构 (1)对于二阶齐次线性微分方程y+P(x)y+Q(x)y=0有如下结论: 定理1如果y(x)与y,(x)是该齐次线性方程的两个解,那么y=Cy,(x)+Cy,(x)也是 该齐次线性方程的解,其中C、C是任意常数 齐次线性方程的这个性质称为解的叠加原理
2 ( ) xdy ydx x d y y − = − , 2 2 (arctan ) xdy ydx y d x y x − = + , 2 2 1 ( ln ) 2 xdy ydx x y d x y x y − + = − − , (ln ) xdy ydx y d xy x − = , 2 2 2 2 ( ) xydy y dx y d x x − = , 2 2 2 2 ( ) xydx x dy x d y y − = . (三)可降阶的高阶微分方程 下面介绍三种容易降阶的高阶微分方程的求解方法. 1. ( ) ( ) n y f x = 型的微分方程 对此方程两边连续积分 n 次,每积分一次增加一个任意常数,便得此方程的含有 n 个任 意常数的通解. 2. y f x y = ( , ) 型的微分方程 此方程的特点是方程中不显含 y ,设 y p = ,则有 dp y p dx = = ,那么原方程转化为一 阶方程 p f x p = ( , ) ,这是关于 x 、 p 的一阶微分方程,求出其通解 1 p x C = ( , ) ,即得到另 一个一阶方程 1 y x C = ( , ) ,两边积分即可得到原方程的通解为 1 2 y x C dx C = + ( , ) ,其中 C1 、 C2 是任意常数. 3. y f y y = ( , ) 型的微分方程 此方程的特点是方程中不显含自变量 x ,令 y p = ,则有 dp dp dy dp y p dx dy dx dy = = = , 原方程转化为 ( , ) dp p f y p dy = ,这是关于变量 y 、 p 的一阶微分方程,设求出的通解为 1 y p y C = = ( , ) ,此方程为变量可分离的方程,分离变量然后积分即可得到原方程的通解为 2 1 ( , ) dy x C y C = + ,其中 C1 、C2 是任意常数. (四)高阶线性微分方程 1.线性微分方程的解的结构 (1)对于二阶齐次线性微分方程 y P x y Q x y + + = ( ) ( ) 0 有如下结论: 定理 1 如果 1 y x( ) 与 2 y x( ) 是该齐次线性方程的两个解,那么 1 1 2 2 y C y x C y x = + ( ) ( ) 也是 该齐次线性方程的解,其中 C1 、C2 是任意常数. 齐次线性方程的这个性质称为解的叠加原理.