
84-2梁的剪力和弯矩·剪力图和弯矩图I、梁的剪力和弯矩F(I-a)AaFAFFBmFaBA合m1Xy取左侧分离体分析任一横截面m-mFm M上的内力F(l-a)CLEF,=0 F=F -AmFsx1F(l-a)ZM。=0 M=F,x=1
§4-2 梁的剪力和弯矩•剪力图和弯矩图 Ⅰ、梁的剪力和弯矩 ( ) l F l a FA − = 取左侧分离体分析任一横截面m-m 上的内力 ( ) l F l a F FA − S = = l Fa FB = ( ) x l F l a M F xA − = = m x m a A B F FB FA FA FS y A m m x x C M Fy = 0 MC = 0

由其右边分离体的平衡条件同样可得IFaFFBZF,=0mBAFs-F+F,=0imTOXF(l-a)yFs= F- F.RFA1mMLyt切向应力的合力C称为剪力mXFFs1DmZM。=0MCBm-M- F(α-x)+ F.(I - x)=0M=F,(l-x)-F(a-x)- F(l-α)vi法向应力的合力,称为弯矩
由其右边分离体的平衡条件同样可得 Fy = 0 MC = 0 ( ) l F l a F F FB − S = − = FS − F + FB = 0 − M − F(a − x)+ FB (l − x) = 0 切向应力的合力, 称为剪力 法向应力的合力,称为弯矩 ( ) ( ) ( ) x l F l a M F l x F a x B − = − − − = a m x m A B F FB FA FA FS y A m m x x C M M FS m F m B C FB
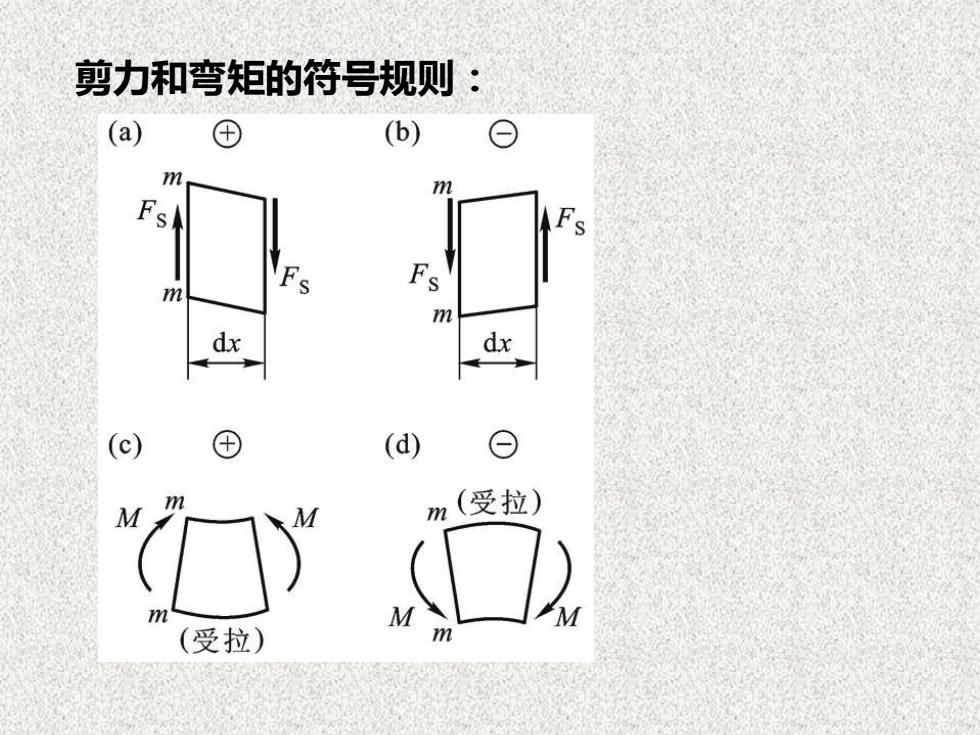
剪力和弯矩的符号规则:④(b)O(a)mmFsAFsFsFsmmdxdx④O(c)(d)m (受拉)mMMMMmm(受拉)
剪力和弯矩的符号规则:

例4-2 求图示外伸梁在截面1--1、2~-2、33和44横截面上的剪力和弯矩。tyM.-3FaFB1A231.41.8.2福3245aOTFBLF2a解:支反力为ZM,=0F,×2a+3Fa+ F×a=0F: = -2F(1)ZF,=0F + F = FF, = 3F(T)
例4-2 求图示外伸梁在截面1—1、2—2、3—3和 4—4横截面上的剪力和弯矩。 解:支反力为 Fy = 0 M A = 0 FB 2a +3Fa + F a = 0 F = −2F() B FB + FA = F F = 3F() A x y A F B a a 2a 1 1 2 2 4 4 3 3 Me =3Fa FA FB
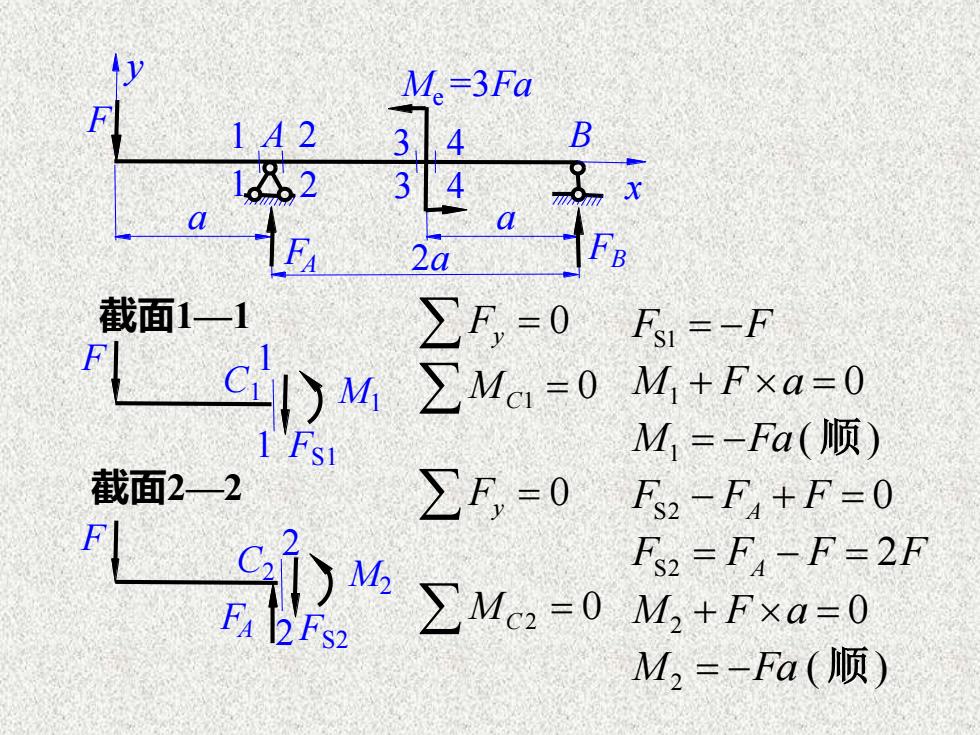
tyM=3FaF1A2B3/.41.8.241x3aaTFBLEA2a截面1—1ZF,=0Fst =--F宾FclM +Fxa=0ZMci=0 LI)MiM,=-Fa(顺)1 Fs1截面2——2ZF,=0 F,-F,+F-0F2Fs2 -F-F=2FC2MIMc=0 M,+Fxa=0FA /2Fs2M,=-Fα(顺)
截面1—1 Fy = 0 MC1 = 0 M1 + F a = 0 ( ) M1 = −Fa 顺 FS1 = −F 截面2—2 Fy = 0 MC2 = 0 M2 + F a = 0 ( ) M2 = −Fa 顺 FS2 − FA + F = 0 FS2 = FA − F = 2F M1 FS1 F C1 1 1 FA M2 FS2 F C2 2 2 x y A F B a a 2a 1 1 2 2 4 4 3 3 Me =3Fa FA FB