3静定梁和超静定梁静定梁梁的支反力均可由平面力系的三个独立的平衡方程求出。超静定梁梁的支反力单独利用平衡方程不能确定MAAOBFxFFB金毛十
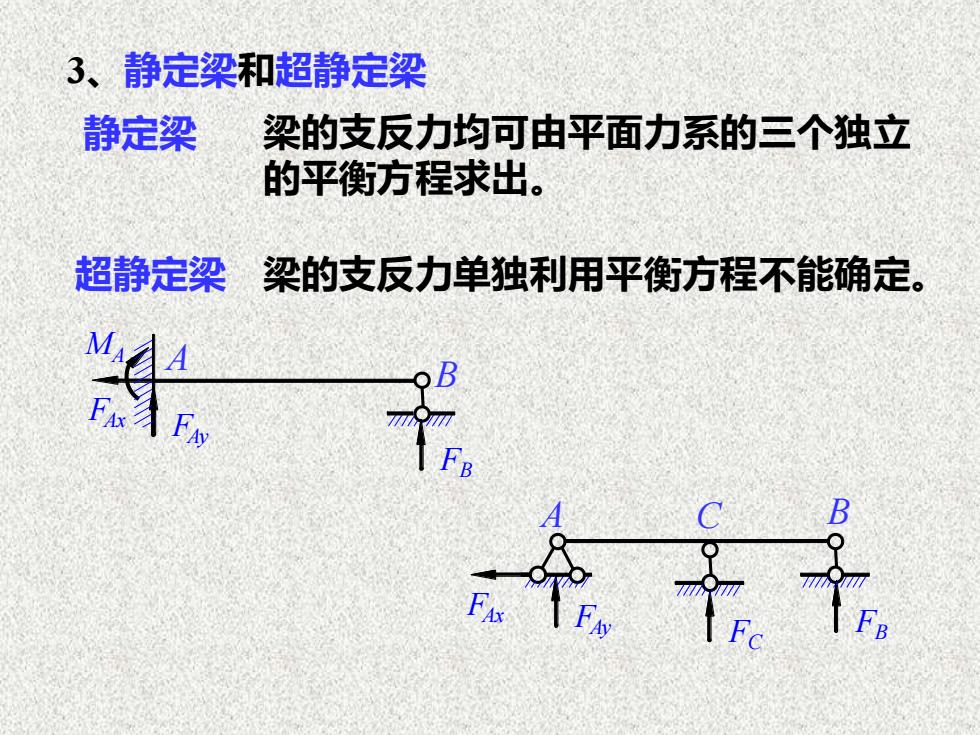
梁的支反力均可由平面力系的三个独立 的平衡方程求出。 3、静定梁和超静定梁 梁的支反力单独利用平衡方程不能确定。 静定梁 超静定梁 FAy FAx MA FB FAy FAx FC FB A B A C B
例4-1 试求图示有中间铰C的梁AB的支反力。q=20kN/mF-50kNM.=5kN m家营发营发BPDKAE3m1m1m1m0.5m解:整体分析梁的受力如图q =20kN/mMM.-5kN m家管发服发家发发家家公BA2DKEFByFA未知支反力:4个整体独立平衡方程:3个关键在于中间铰不能传递力矩的特性,因而不论AC段或CB段均有ZMc=0
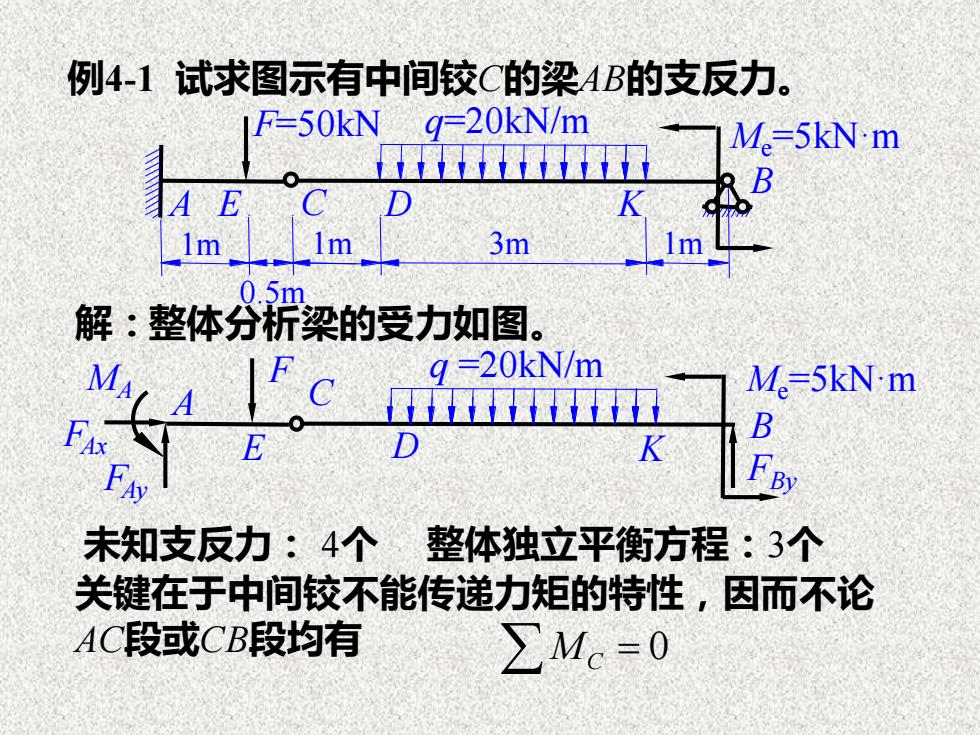
例4-1 试求图示有中间铰C的梁AB的支反力。 关键在于中间铰不能传递力矩的特性,因而不论 AC段或CB段均有 解:整体分析梁的受力如图。 未知支反力: 4个 整体独立平衡方程:3个 MC = 0 1m 0.5m 1m 3m 1m B A E C D K F=50kN q=20kN/m Me=5kN·m FBy MA FAx FAy C D K q =20kN/m Me=5kN·m A E F B

q=20kN/mF=50kNM.-5kN m武#BKDECA3m1m1m1m0.5mFcy50kNMZMc=0AFcxEFAxHA1q =20kN/mM.-5kN m家rDKFcxFByFcyZMc=0 -(20×103×3×2.5)+5×10° +Fg×5=0Fby = 29kN
MC = 0 MC = 0 FCx FCy A C E 50kN FCy ' FCx ' MA FAx FAy 1m 0.5m 1m 3m 1m B A E C D K F=50kN q=20kN/m Me=5kN·m D K q =20kN/m C FBy Me=5kN·m FBy = 29kN (20 10 3 2.5) 5 10 5 0 3 3 − + + FBy =
q =20kN/mIFMM.-5kN mCA#营童营BOFAxDKEFbyFAy3m1m1m1m0.5mFx =0ZF=0ZF, =0- FA, + 50 + (20×3)- 29 = 0Fa, - 81kN(0)EM, =0M -50×103×1+5×103-20×103 ×4×3= 0M. = 96.5kN·m
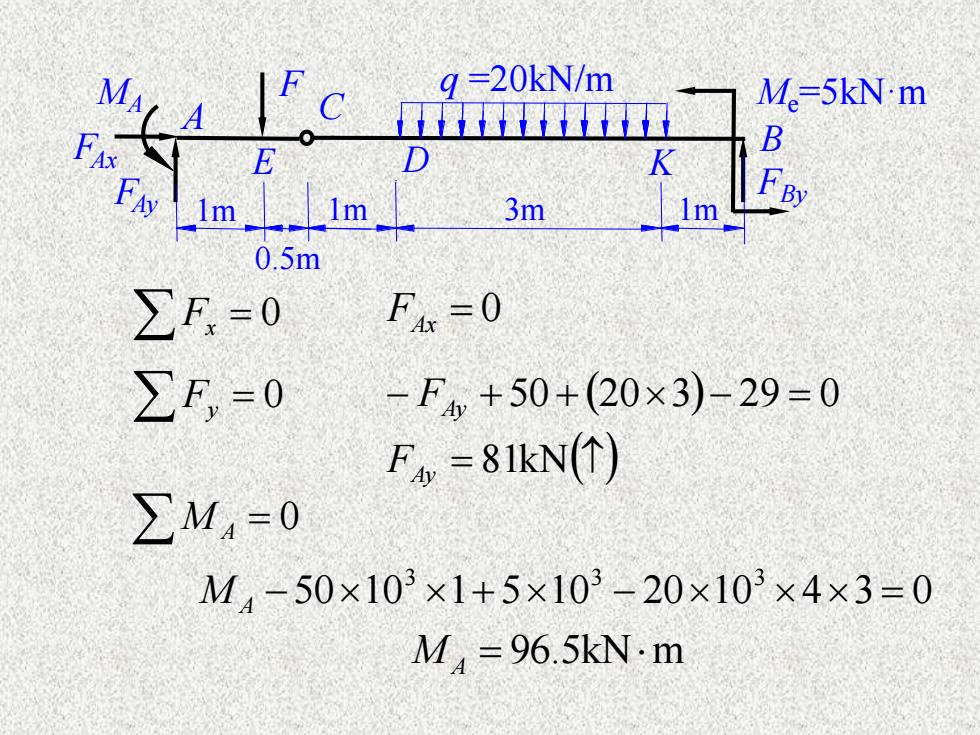
Fx = 0 = 81kN() FAyMA = 96.5kNm M A = 0 Fy = 0 FAx = 0 − FAy + 50 + (203)− 29 = 0 50 10 1 5 10 20 10 4 3 0 3 3 3 M A − + − = FBy MA FAx FAy C D K q =20kN/m Me=5kN·m A E F B 1m 0.5m 1m 3m 1m

带有中间铰的梁的受力特点:FcyMFcxEFFAxq =20kN/mM-5kN mTBDKFC[FByFcyCB梁段上的荷载会传递到梁的AC段,称为副梁AC段上的荷载不会传递到梁的CB段,称为基本梁(或主梁)
CB梁段上的荷载会传递到梁的AC段,称为副梁; AC段上的荷载不会传递到梁的CB段,称为基本 梁(或主梁)。 C FCx FCy A E F FCy ' FCx ' MA FAx FAy D K q =20kN/m C FBy Me=5kN·m 带有中间铰的梁的受力特点: B