
4.5正弦稳态电路的功率 情形2:Z阻抗角不变,仅模值可变 平均功率 P=R12= RUR (R+R)2+(X、+X)2 设Z2=R+jX,Z|∠0其中0固定,Z,1可变 →P UZ,|cose R+X3+R+X2+2R·R+2Xs·Xz IZsP U cose IZLlcose IZLlsin0 P-jZ,FAZI+Z+2R.cos@+2X,sim0 变量 由 dP =0Z,HZ时,P= U2 cos0 d z,| 2|Z、|+2(Rcos0+X、sin0) 在该情形中,获得最大功率的条件为Z=Z$ 模匹配!
4.5 正弦稳态电路的功率 情形2:ZL阻抗角不变,仅模值可变 2 2 S L 2 2 S L L S L ( ) ( ) 平均功率 U P R I R X R R X = = + + + 2 2 | 2 2 | S co | 2 s |s 2 | | n | i 2 | | 2 2 | cos L L S L S S L S L S L Z L Z Z L Z R X R X U P R X R X Z → = + + + + + | | | | 设Z jX Z L L L L L = = R Z + ,其中 固定, 可变 2 2 S | | | o cos | | / 2 | c s 2 sin 变量 S S S L L U Z Z X P Z R → = + + + 2 m cos 2 | | 2( cos sin ) d =0 | | | | d | | 由 时, S S S L S S L P Z Z Z U P Z R X + + → = = 在该情形中,获得最大功率的条件为|ZL |=|ZS | 模匹配!

4.5正弦稳态电路的功率 总结:最大功率传输条件 ·若负载阻抗中,电阻、电抗可独立变化,最大功率传输 条件为“共轭匹配”: Z=Zs 若仅模值可变,阻抗角不变,最大功率传输条件为“模 匹配”: IZ,HZsI 思考:若负载为纯电阻呢? 依旧为模匹配! →1Z曰Z→RZI
4.5 正弦稳态电路的功率 总结:最大功率传输条件 • 若负载阻抗中,电阻、电抗可独立变化,最大功率传输 条件为“共轭匹配” : • 若仅模值可变,阻抗角不变,最大功率传输条件为“模 匹配” : Z Z L S = | | | | Z Z L S = 思考:若负载为纯电阻呢? 依旧为模匹配! | | | | | | ZL = → ZS RL S = Z

4.5正弦稳态电路的功率 例在下列情况下,如何选择负载Z才能使负载吸收的功率最大,并求出最大 功率? (1)Z为可变阻抗 j52 (2)Z为可变纯电阻 2/0° 52 解戴维南等效。 j102 Uoc=(仁j10/5)i3=(4-j2)i、=4V5L-26.6(W) Zg=j5+51(-j10)=4+j3=5∠36.9 (1)Z=Zg=4-j32, Uc-(4W5)2 4×4 =5W) (2)Z=R=|Zg1=52 Pim 12RL= U 4V5 R ×5≈4.44W 14+3j+5
例 在下列情况下,如何选择负载ZL才能使负载吸收的功率最大,并求出最大 功率? (1) ZL为可变阻抗 (2) ZL 为可变纯电阻 -j10Ω j5Ω 5Ω ZL S I 2/0°A 解 戴维南等效。 U ( j1 0 / / 5 ) I ( 4 j 2 ) I 4 5 2 6 .6 (V ) O C S S = − = − = − Z = j 5 + 5 // (− j1 0 ) = 4 + j 3 = 5 3 6 .9 e q (1) ZL = Zeq * = 4 – j3Ω, 5(W) 4 4 (4 5 ) 4 2 2 max = = = e q O C L R U P (2) ZL = RL = | Zeq | = 5 Ω 4.5 正弦稳态电路的功率 2 2 2 4 5 5 4.44 W | | | 4 3 5 | S Lm L L eq L U P I R R Z R j = = = + + +
4.5正弦稳态电路的功率 多频电路的响应和平均功率 电路分析中,常会遇到几个不同频率的电源作用于电路的情况,这时, 求电压、电流时可利用叠加定理。平均功率也可叠加计算。 例:如图电路,L=1H,C=1F,R=12,s1()=10cos)V, us2()=10Cos(2)V,求电流()和电阻R吸收的平均功率PR 注意:相量法只适 用于单频激励,此 处两个不同频率, 如何是好啊?
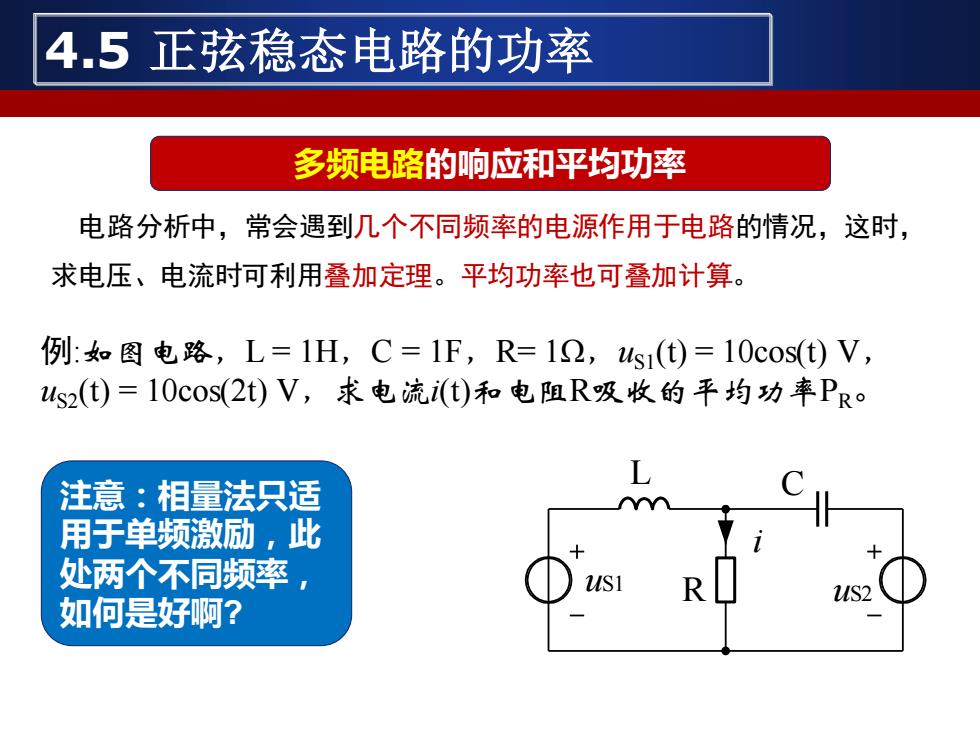
电路分析中,常会遇到几个不同频率的电源作用于电路的情况,这时, 求电压、电流时可利用叠加定理。平均功率也可叠加计算。 R L C uS1 uS2 i 例:如图电路,L = 1H,C = 1F,R= 1Ω,uS1(t) = 10cos(t) V, uS2(t) = 10cos(2t) V,求电流i(t)和电阻R吸收的平均功率PR。 4.5 正弦稳态电路的功率 多频电路的响应和平均功率 注意:相量法只适 用于单频激励,此 处两个不同频率, 如何是好啊?

4.5正弦稳态电路的功率 利用叠加定理:s1(①)单独作用时, 画出相量模型。 i,=0 1/1-j 1→i,=5√2∠-90 j+(1/1-) 分压 故i1()=10c0s(t-90°)As2()单独作用时,画出相量模型。 1/2j 1,=0s0.5j+112] 337 -j0.5 分压 故i2()=11c0s(2t+33.7°)A. i(t)=i(t)+i2()=10cos(t-90°)+11c0s2t+33.7°)A
1 j -j US1 1 I 1 j2 -j0.5 US 2 2 I 利用叠加定理: uS1(t) 单独作用时, 画出相量模型。 故 i2 (t) = 11cos(2t + 33.7°) A。 故 i1 (t) = 10cos(t-90°) A i(t) = i1 (t) + i2 (t) = 10cos(t - 90°) + 11cos(2t + 33.7°) A uS2(t) 单独作用时,画出相量模型。 4.5 正弦稳态电路的功率 1 1 1 1/ / 1 (1/ ) 2 0 / 5 9 分压 S j I j U j I − = − − + → = 2 2 2 1/ /2 1 0.5 1/ / 2 11 33.7 2 分压 S j U j j I I → = − = +