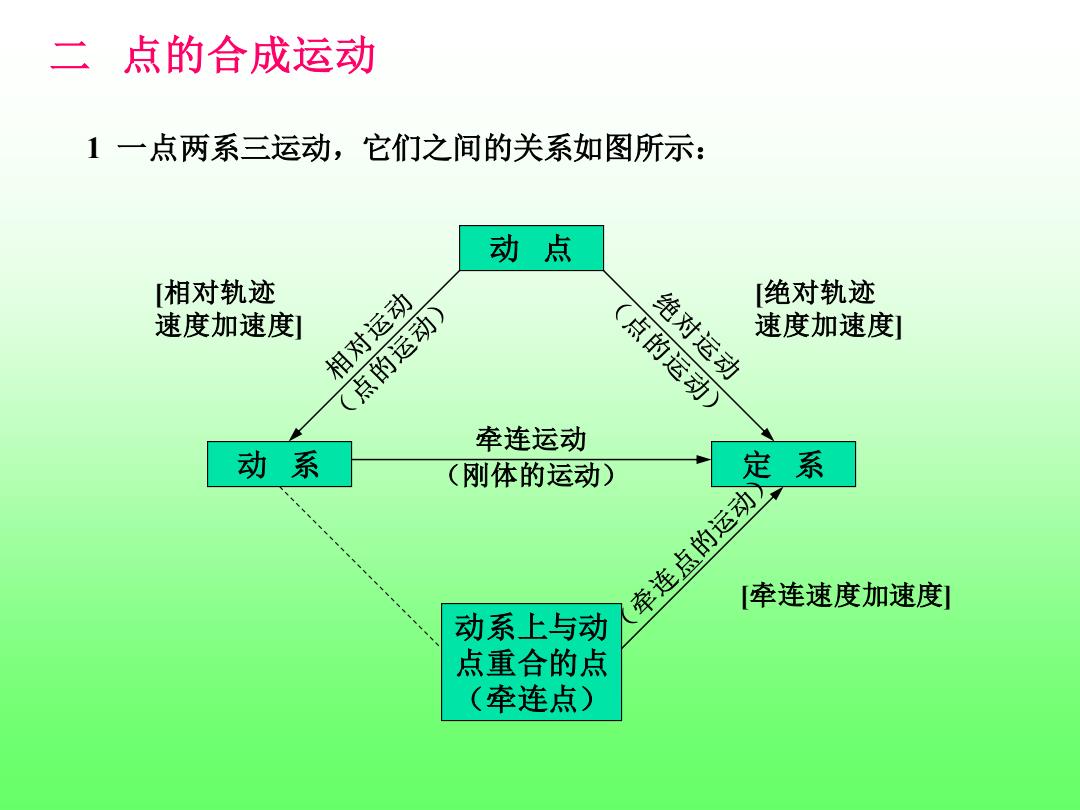
二点的合成运动 1一点两系三运动,它们之间的关系如图所示: 动点 「相对轨迹 绝对轨迹 速度加速度] 相对运动 (点的运动) 绝对运动 (点的运动) 速度加速度引 牵连运动 动系 (刚体的运动) 定系 牵连点的运动 牵连速度加速度] 动系上与动 点重合的点 (牵连点)
二 点的合成运动 1 一点两系三运动,它们之间的关系如图所示: 动 点 动 系 定 系 动系上与动 点重合的点 (牵连点) 牵连运动 (刚体的运动) [相对轨迹 速度加速度] [绝对轨迹 速度加速度] [牵连速度加速度]

2动点动系的选取原则 动点动系不能同时固连在同一个刚体上,否则动点与动系之 间就不会有相对运动,也就不能构成点的合成运动。 动点相对于动系的相对运动轨迹要明显,简单(比如轨迹是 直线、圆或某一确定的曲线),并且动系要有明确的运动 (比如平动、定轴转动或平面运动)。 3速度合成定理:三种速度间的关系。 。=。+ 绝对速度在平行四边形的对角线方向。 4牵连运动为平动时的加速度合成定理: ea。+d 普遍形式 加速度合成定理中加速度要素的个数可以为3、4、5、6个,当为3 个时,用平行四边形法,当大于3个时,用投影法
2 动点动系的选取原则 • 动点动系不能同时固连在同一个刚体上,否则动点与动系之 间就不会有相对运动,也就不能构成点的合成运动。 • 动点相对于动系的相对运动轨迹要明显,简单(比如轨迹是 直线、圆或某一确定的曲线),并且动系要有明确的运动 (比如平动、定轴转动或平面运动)。 3 速度合成定理:三种速度间的关系。 a e r v v v = + 4 牵连运动为平动时的加速度合成定理: 绝对速度在平行四边形的对角线方向。 aa ae ar = + 普遍形式 加速度合成定理中加速度要素的个数可以为3、4、5、6个,当为3 个时,用平行四边形法,当大于3个时,用投影法
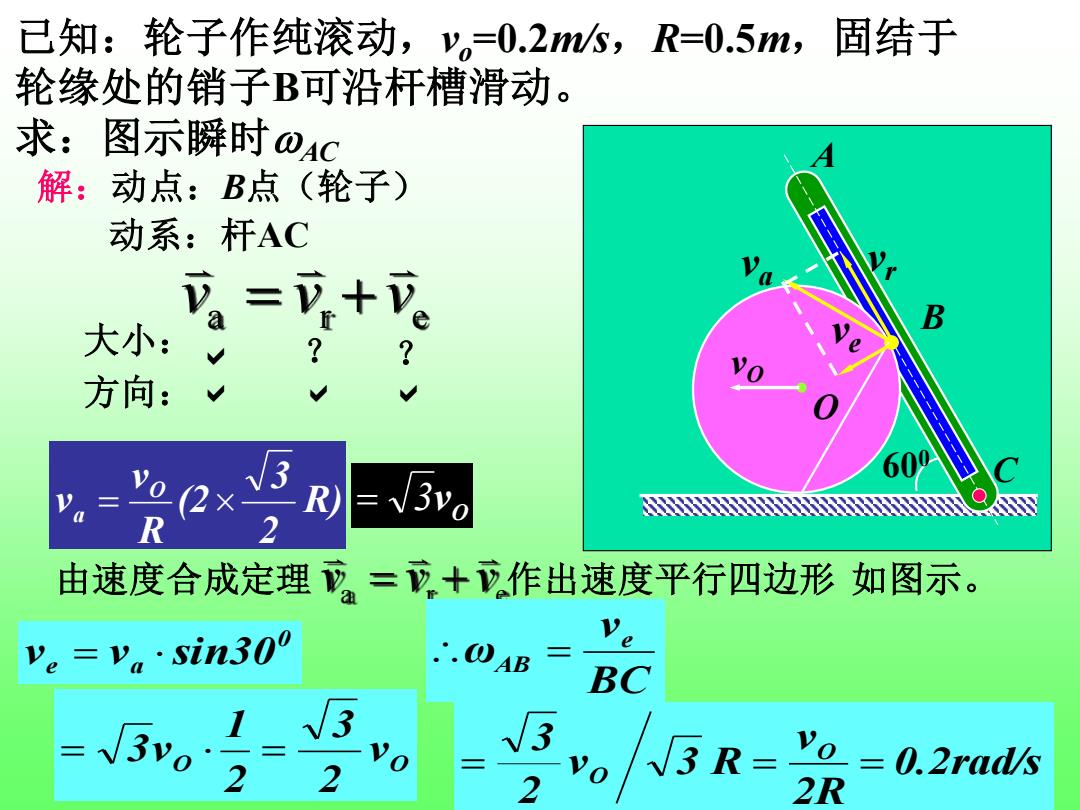
已知:轮子作纯滚动,v。=0.25,R=0.5m,固结于 轮缘处的销子B可沿杆槽滑动。 求:图示瞬时O4C 解:动点:B点(轮子) 动系:杆AC 可=+ 大小: ? 方向: 3 2x R 0 R 2 由速度合成定理=,十作出速度平行四边形如图示。 Ve=va·Sin300 ..OAB e BC √3 0 90 3 R= Yo =0.2rad/s 2 2R
已知:轮子作纯滚动,vo=0.2m/s,R=0.5m,固结于 轮缘处的销子B可沿杆槽滑动。 求:图示瞬时AC 解:动点:B点(轮子) 动系:杆AC 0 e a v = v sin30 0.2rad/s 2R v v 3 R 2 3 O = O = = 大小: 方向: ? ? 由速度合成定理 va vr ve 作出速度平行四边形 如图示。 = + a r e v v v = + A B O C vO 600 va vr ve R) 2 3 (2 R v v O a = O = 3v O O v 2 3 2 1 = 3v = BC v ω e AB =
B B B R 7777777w7777777277777772 偏心凸轮机构 B A 0 0 B
φ A B CO DM ω θ CB O A x y o